Лабораторна робота 9 Визначення питомої теплоємності металів методом охолодження

Прилади та матеріали: електропіч, еталонний та досліджувані зразки металів, секундомір, цифровий вольтметр, ЛАТР.

Теоретичні відомості

Найажливіша характеристика металів – теплоємність. Її визначають відношенням кількості теплоти ΔQ , підведеної до тіла, до викликаного цим теплом підвищення температури ΔT:

. (9.1)

Отже, для визначення теплоємності С необхідно підвести до досліджуваного зразка металу певну кількість тепла ΔQ або відвести його і виміряти пов'язану з цим зміну температури ΔT. Однак, якщо ΔT легко знайти з високою точністю, то вимірювання ΔQ пов’язане з певними експериментальними труднощами. Тому в даній роботі вимірювання ΔQ виключено, а теплоємність С визначають непрямим методом.

Якщо металевий зразок нагріти до температури, яка перевищує температуру навколишнього середовища, то протягом деякого часу він буде охолоджуватися, причому швидкість охолодження буде залежати від температури зразка і його питомої теплоємності.

Доведемо, що порівнюючи криві охолодження двох зразків і знаючи теплоємність одного (еталона), можна визначити питому теплоємність іншого.

Елементарний об'єм металу ΔV під час охолодження за час Δτ втрачає кількість теплоти

, (9.2)

де С – питома теплоємність металу; ρ – густина металу; Δt/Δτ – швидкість охо­лодження.

У зв’язку з незначними розмірами і високою теплопровідністю металу температуру в усьому об’ємі зразка можна вважати однаковою в будь-який момент часу. Отже, С, Δt/Δτ і ρ не залежать від координат точок об'єму зразка. У цьому випадку весь зразок об'ємом V за час втрачає таку кількість тепла:

. (9.3)

Це тепло йде в навколишнє середовище з поверхні S зразка. Кількість тепла, яка втрачається з елемента поверхні зразка ΔS за час τ, знаходять за відомим співвідношенням Ньютона:

, (9.4)

де α – коефіцієнт тепловіддачі, який чисельно дорівнює кількості тепла пере­даного одиницею поверхні зразка за одиницю часу за умов різниці між температу­рами поверхні тіла й навколишнього середовища 1⁰ С; t – температура зразка; t₀ –температура навколишнього середовища.

Якщо вважати, що α, t і t₀ залежать від координат точок поверхні зразка, то кількість тепла, втраченого всією поверхнею за час τ, дорівнює

. (9.5)

Прирівнюючи праві частини рівнянь (19.3) і (19.5), одержимо

(9.6)

або після скорочення на τ

. (9.7)

Кількість тепла, втраченого поверхнею зразка, визначають лише за станом поверхні й різницею температур поверхні зразка й навколишнього середовища.

Візьмемо два зразки однакової форми й розмірів і будемо нагрівати їх до однакової температури; для зразків маємо

V₁ = V₂; S₁ = S₂; a₁ = a₂; t₁ = t₂ . (9.8)

На підставі формули (9.7) запишемо рівняння для зразків:

а) еталонного –

; (9.9)

б) досліджуваного –

. (9.10)

Враховуючи рівності (9.8), поділимо почленно рівняння (9.9) на рівняння (9.10), одержимо

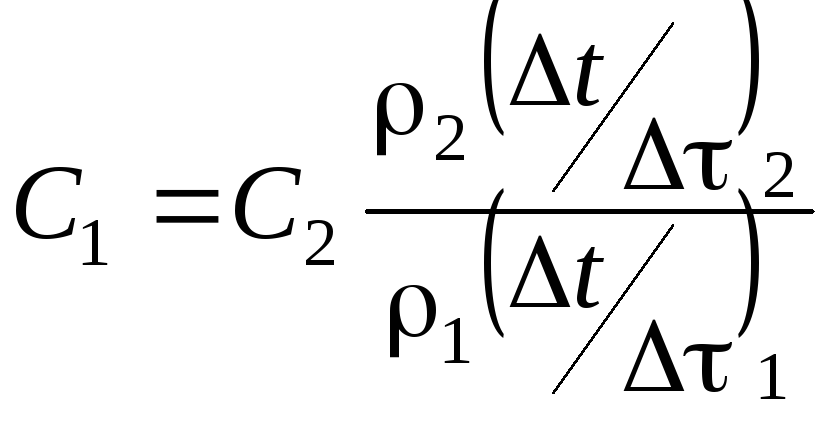, (9.11)

де ρ₁ і ρ₂, –густини досліджуваного й еталонного зразків відповідно; С₁ і С₂ – теплоємності досліджуваного й еталонного зразків відповідно. ,– швидкість охолодження зразків.

Беручи до уваги, що ,, деm₁ i m₂ – маси досліджуваного й еталонного зразків відповідно, одержимо остаточний вираз для знаход­ження питомої теплоємності досліджуваного зразка:

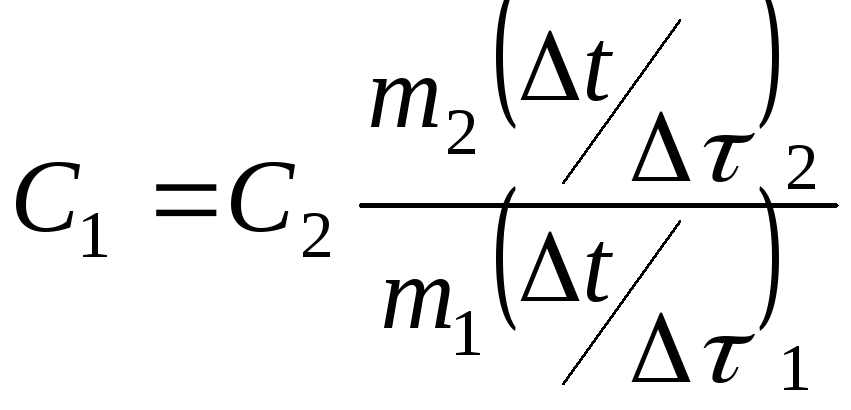. (9.12)