Теоретичні відомості

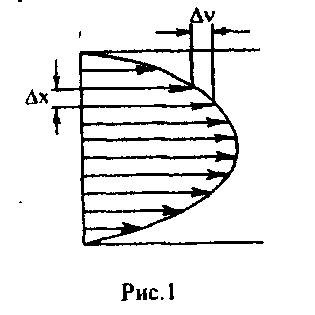
Якщо розглядати ламінарний потік рідини по трубі, то розподіл швидкостей у перерізі цієї труби буде мати вигляд, поданий нижче (рис.7.1). При цьому шар рідини, який прилягає безпосередньо до стінки труби, ніби прилипає до неї і його швидкість дорівнює нулю. Найбільшу швидкість мають шари, розмі­щені вздовж осі труби. Ця різниця швидкостей пов’язана з тертям шарів рідини одного об оден, яке називають внутрішнім тертям. Із боку швидкого шару на шар, який рухається повільніше, діє прискорювальна сила. І навпаки, з боку повільного шару на швидкий діє гальмуюча сила. Причина внутрішнього тертя – обмін молеку­лами між сусідніми шарами рі­дини.

Н

Рис. 7.1

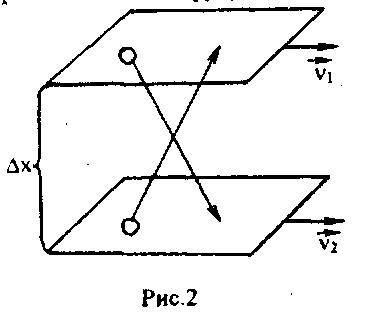
ехай два шари рідини (рис.7.2), розташовані один від одного на відстаніх , рухаються з різ­ними швидкостями v₁ і v₂ (v₁ >v₂). Імпульс молекул кожного шару обумовлений як хаотичним тепловим рухом молекул, так і впорядкованим. Завдяки тепловому руху молекули пере­ходять із шару в шар, при цьому з шару 2 у шар 1 молекули переносять свій ім­пульс упорядкованого руху mv₂ , а з шару 1 у шар 2 – mv₁. Молекули шару 2 пе­реходять у шар 1 і, зіткнувшись із його молекулами, уповільнюють швид­кість їх упорядкованого руху (швидкість шару), а молекули шару 1, опинившись у шарі 2, прискорюють швидкість останнього. Силу внутрішнього тертя, яка виникає при цьому, можна ви­значити за формулою Ньютона:

, (7.1)

д

1

еS– площа поверхні поділу між двома сусідніми шарами; η – коефіцієнт внутрішнього тертя, який залежить від природи, тем­ператури й тиску рідини; – градієнт швидкості, який характеризує зміну швидкості руху шарів на оди­ницю довжини в напрямку нормалі до їх поверхні.

Сила внутрішнього тертя направлена по дотичній до поверхні шарів у бік, протилежний до їх руху ( на це, до речі, вказує знак “мінус” ).

К

Рис.7.2

2

оефіцієнтη чисельно дорівнює силі внутрі­шнього тертя, що виникає на кожному квадратному метрі поверхні поділу двох су­сідніх шарів, якщо їх швидкість змінюється на 1 м/с на кожному метрі відстані між ними. У між­народній системі СІ одиниця вимірювання в’язкості – кг/(м∙с).

К

Рис. 7.2

оефіцієнт внутрішнього тертя сильно зале­жить від температури: для рідини він знижується із підвищенням температури, для газів навпаки.

На тверді тіла, які рухаються в рідині, діє опір. У разі невели­ких швидкостей сила опору обумовлена в'язкістю рідини.

В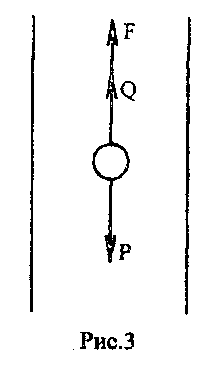изначення коефіцієнта в'язкості за методом Стокса засно­ване на вивченні руху кульки у в'язкій рідині. У досліджувану рідину кидають маленьку тверду кульку. Шар рі­дини, що вкриває її поверхню і рухається з такою самою швидкістю, зазнає опору з боку прилеглих до нього інших шарів. Цей опір зумовлений внутрішнім тертям рідини.

Рис. 7.3

Кулька, що рухається у в'язкій рідині, перебуває під дією трьох сил: ваги Р, підіймальної сили Q, що виникає за законом Архі­меда, і сили в’язкості F, яка за законом Стокса прямо пропор­ційна радіусу кульки r, швидкості її руху v та коефіцієнту внутрішнього тертя η (рис 7.3):

. (7.2)

Під час падіння в нескінченну в усіх напрямках в’язку рідину кулька, рухаючись прискорено, набуває такої швидкості, за якої сили, що діють на неї, взаємно врі­вноважуються. У такому випадку має місце рівняння

або

, (7.3)

де ρ – густина кульки; ρ₀ – густина досліджуваної рідини ( за певної темпера­тури).

У разі рівноваги всіх сил, що діють на кульку, її подальший рух стає рівномірний.

Розв'язавши рівняння ( 7.3), відносно η, одержимо

. (7.4)

Швидкість кульки v можна знайти, знаючи час τ проходження нею певного шляху L. Тоді рівняння (7.4) буде мати вигляд

. (7.5)

Рівняння (7.5) правдиве тільки тоді, коли кулька падає в нескінченне середовище. У випадку вимірювання коефіцієнта в'язкості за методом Стокса у формулу (7.5) вносять поправку, якою враховують вплив стінок циліндра:

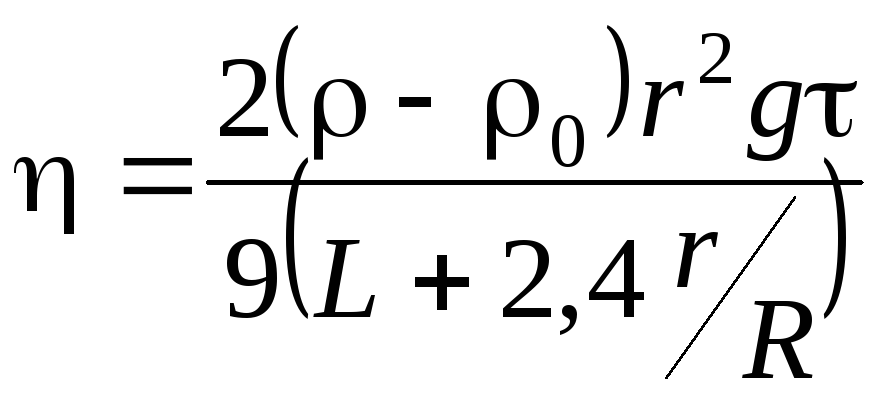, (7.6)

де R– внутрішній радіус циліндра.

За умови малих значень відношення R/r (R/r <10^-3 ) можна застосовувати фор­мулу (7.5).