7. Комплексно-спряжені числа

Означення.Числа виглядутаназиваються комплексно-спряженими.

Очевидно, що сума і добуток комплексно-спряжених чисел

,

.

є дійними числами.

Відмітимо важливі для подальшого властивості.

Властивість 1.Число комплексно-спряжене до суми дорівнює сумі чисел спряжених до доданків.

.

Доведення.Нехай,, тоді. Тому.

Аналогічно можна довести (пропонується зробити це самостійно):

1. ;

2. ;

3. .

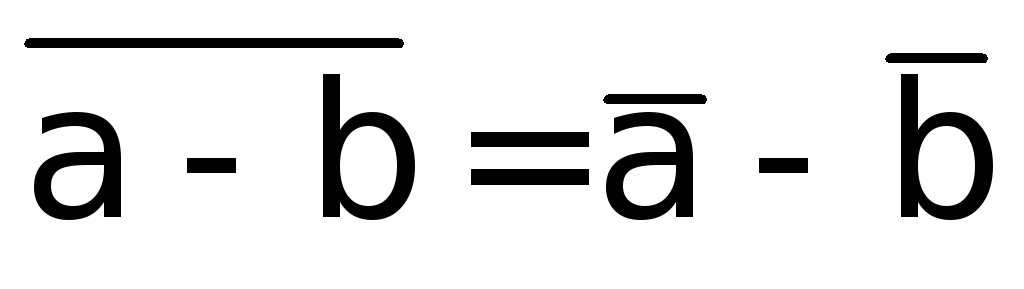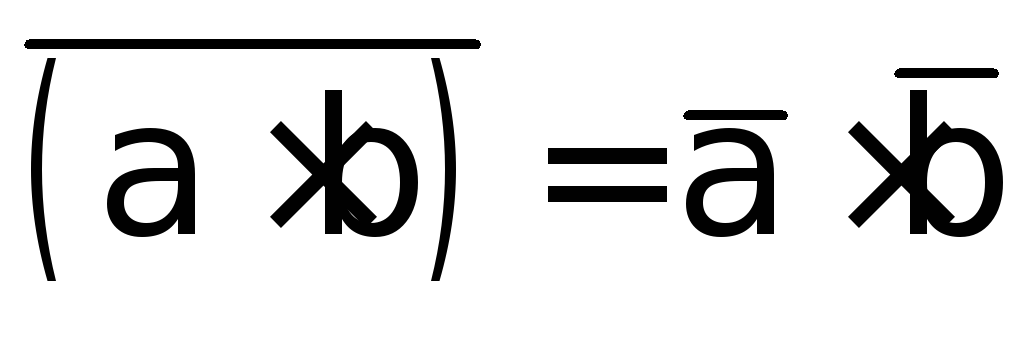8. Нерівність трикутника

Як і для дійсних чисел для комплексних чисел має місце нерівність трикутника

Доведення.Спочатку доведемо геометрично, що.

Зобразимо на площині комплексні числа та, побудуємо геометрично суму. Отримаємо трикутникзі сторонами

Тоді, за нерівністю трикутника маємо

.

Отже, друга частина нерівності доведена.

Доведення першої частини нерівності зведемо до другої частини. Для цього запишемо очевиднунерівность.

,

Застосуємо до цієї суми доведену нерівність

.

Зауважимо, що (довести самостійно). Тоді маємо нерівність в області дійсних чисел

.

А тому,

,

що і треба було довести.

Якщо в нерівності трикутника покласти , то отримаємо і таку нерівність.

7. Література

1. Ильин В.А. Аналитическая геометрия/В.А.Ильин, Э.Г.Позняк. – М.:Наука, 1971. – 232с.

2. Ильин В.А. Линейная алгебра/В.А.Ильин, Э.Г.Позняк. – М.:Наука, 1984. – 232с.

3. Завало С.Т. Курс алгебри. – К.: Вища шк., 1985. – 504с.

4. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.:Наука, 1979. – 512с.

5. Курош А.Г. Курс высшей алгебры. – М.:Наука, 1975. – 431с.

6. Моденов П.С. Аналитическая геометрия. – М.: Изд-во МГУ, 1969. – 670с.

7. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1984. – 320с.

8. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. – М.: Гостехиздат, 1949. – 336с.

9. Тышкевич Р.И. Линейная алгебра и аналитическая геометрия/ Р.И.Тышкевич, А.С. Феденко. – Минск: Вышейшая школа, 1968. – 505с.

10. Проскуряков И.В. Сборник задач по линейной алгебре. – М.: Наука, 1984. – 336с.

11. Бурдун А.А. Сборник задач по алгебре и аналитической геометрии/ А.А.Бурдун, Е.А.Мурашко, М.М.Толкачев, А.С.Феденко. – Мн.: Універсітэцкае, 1999. – 302с.

12. Гетманцев В.Д. Лінійна алгебра і лінійне програмування. – К: Либідь, 2001. – 256с.

13. Гриньов Б.В. Аналітична геометрія./Б.В.Гриньов, І.К.Кириченко. – Харків: Гімназія, 2008. – 344с.

14. Гриньов Б.В. Вища алгебра./Б.В.Гриньов, І.К.Кириченко. – Харків: Гімназія, 2008. – 184с.

15. Гриньов Б.В. Векторна алгебра./Б.В.Гриньов, І.К.Кириченко. – Харків: Гімназія, 2008. – 164с.

16. Варех Н.В. Лабораторні роботи до курсу лінійної алгебри та геометрії/ Н.В.Варех, М.П.Д’яченко, Н.А.Лихолат, С.Д.Сотникова. – Д.: РВВ ДДУ, 1992. – 52с.

17. Варех Н.В. Методи обчислення визначників n-го порядку/Н.В.Варех, М.П.Д’яченко, В.Б.Круглушина. – Д.: РВВ ДДУ, 1995. – 28с.

18. Варех Н.В. Лінійні оператори/Н.В.Варех, М.П.Д’яченко. – Д.: РВВ ДДУ, 2003. – 28с.

19. Варех Н.В. Методические указания к самостоятельному изучению раздела «Многочлены от одной переменной»/ Н.В.Варех, Н.А.Лихолат, О.М.Ревин, В.Н.Трофимов. – Д.: РВВ ДДУ, 1989. – 32с.

20. Варех Н.В. Методические указания к самостоятельному изучению раздела «Плоскость»/ Н.В.Варех, Н.А.Лихолат, О.М.Ревин, В.Н.Трофимов. – Д.: РВВ ДДУ,. – 1992. – 32с.

21. Варех Н.В. Практикум із дисципліни «Алгебра та геометрія»/Н.В.Варех, М.П.Д’яченко. – Д.: РВВ ДНУ, 2005. – 48с.

22. Варех Н.В. Практикум із дисципліни «Алгебра та геометрія»/Н.В.Варех, М.П.Д’яченко. – Д.: РВВ ДНУ, 2007. – 76с.

23. Варех Н.В. Практикум із векторної алгебри/Н.В.Варех, Н.Л.Козакова. – Д.: РВВ ДНУ, 2007. – 52с.