88

Поданий конспект лекцій курсу "Алгебра та геометрія" за перший семестр навчального року, призначений для студентів всіх спеціальностей першого курсу факультету прикладної математики денної та заочної форми навчання.

За час існування спеціальності "Прикладна математика" у Дніпропетровському національному університеті створено добре збалансований курс "Алгебри та геометрії". Є декілька способів викладання цього курсу. Перший – послідовного викладання аналітичної геометрії, а потім алгебри. Другий шлях – паралельного викладання цих курсів. Третій спосіб – це ретельно продуманий шлях взаємного доповнення та проникнення. На факультеті прикладної математики надається перевага останньому.

Курс починається зі знайомого із шкільних курсів математики та фізики розділу "векторна алгебра". Потім поняття геометричного вектора шляхом формалізації узагальнюється у абстрактний векторний простір. Велика увага приділяється окремому випадку – арифметичному простору. Тим часом на практичних заняттях створюється апарат для розв'язування задач векторної алгебри (визначники другого та третього порядків). Це питання знаходить продовження на лекціях у розділі "Визначники n-го порядку". Таким чином студенти підготовлені до побудови загальної теорії лінійних рівнянь та алгебри матриць. Далі вивчаються комплексні числа, які необхідні для розгляду основної задачі першого етапу розвитку алгебри (задачі розв'язування алгебраїчних рівнянь n-го степеня). Цими питаннями закінчується перший семестр.

При викладанні курсу "Алгебри та геометрія" витримується один із дидактичних принципів: від простого до складного.

Зміст

1 Векторна алгебра 6

1.1 Системи лінійних алгебраїчних рівнянь. Метод послідовного виключення невідомих (метод Гаусса). 6

1.2 Поняття вектора, лінійні операції над векторами. 9

1.3 Поняття лінійно залежних і лінійно незалежних систем векторів. 11

1.4 Геометрична інтерпретація поняття лінійної залежності. 12

1.5 Поняття базису простору і площини 14

1.6 Афінна система координат. 15

1.7 Додатковий матеріал з векторної алгебри 16

1.8 Поняття лінійного простору. 23

1.9 Найпростіші властивості векторного простору. 25

2 Теорія визначників n-го порядку. 26

2.1 Перестановки з n символів. 26

2.2 Підстановки n-го степеня. 28

2.3 Поняття і властивості визначника n-го порядку 29

2.4 Мінори і алгебраїчні доповнення визначника 34

2.5 Лема до теореми Лапласа. Теорема Лапласа. 34

2.6 Застосування теорії визначників до лінійних систем алгебраїчних рівнянь. Теорема Крамера та лема до неї 38

3 Векторний простір 41

3.1 Подальше вивчення векторного простору. 41

3.2 Поняття рангу системи векторів. 44

3.3 Поняття рангу матриці. Теорема про ранг матриці. 46

4 Загальна теорія лінійно-алгебраїчних рівнянь 51

4.1 Критерій сумісності лінійних алгебраїчних рівнянь 51

4.2 Критерій визначеності і невизначеності системи 52

4.3 Однорідна система рівнянь. Фундаментальна система розв'язків однорідної системи рівнянь. 55

4.4 Зв’язок між розв’язком неоднорідної і відповідної однорідної системи рівнянь. 59

5 Алгебра матриць 61

5.1 Множиння матриць. 61

5.2 Матриці обернені до даних. Умови їх існування. 65

5.3 Операції додавання і множення на число. 67

5.4 Скалярні матриці. 71

5.5 Операції над прямокутними матрицями. 72

5.6 Псевдообернені матриці. 72

6 Комплесні числа. 76

6.1 Побудова множини комплексних чисел. 76

6.2 Полярна система координат. 79

6.3 Тригонометрична форма комплексного числа. Операції множення та ділення в тригонометричній формі. 81

6.4 Операції піднесення до степеня 82

6.5 Операція здобуття кореня n-ого степеня з комплексного числа 83

6.6 Корені n-ого степеня з одниці 85

6.7 Комплексно-спряжені числа 86

6.8 Нерівність трикутника 86

7 Література 88

1. Векторна алгебра

Одним з важливих розділів даного курсу є загальна теорія лінійних алгебраїчних рівнянь. Ця теорія ґрунтується на понятті рангу системи векторів, арифметичному просторі. Тому попередньо слід вивчити векторний простір і пов’язані з ним поняття лінійної залежності, базису. Поняття абстрактного векторного простору є природним узагальненням геометричного простору, який в деякому ступеню вивчався в середній школі під назвою площина і простір. Але в шкільному курсі формально-алгебраїчний підхід до "вектора" ґрунтувався на прямокутних координатах точок (кінця і початку) вектора, (тобто первинним було поняття координат точки). В даному курсі розглядається інша концепція, яка приводить до узагальнення поняття площини, простору, до n-вимірного векторного простору.

При розгляданні "Векторної алгебри" на площині і в просторі, доведеться розв’язувати систему лінійних алгебраїчних рівнянь, тому ми почнемо з методу Гаусса, розв’язування таких систем. Цей метод не потребує попередніх знань.

1. Системи лінійних алгебраїчних рівнянь. Метод послідовного виключення невідомих (метод Гаусса).

Запишемо загальну систему лінійних алгебраїчних рівнянь. Домовимось позначати коефіцієнти при невідомих . Перший індекс вказує номер рівняння, другий індекс – номер невідомого. Невідомі (змінні) позначатимемо буквами , а вільні члени – .

Тоді систему рівнянь з невідомими можна записати у вигляді:

(1)

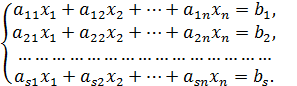
Означення 1.Розв’язком системи (1) називається упорядкована системаnчисел, після підстановки яких замістьвідповідно, кожне рівняння перетворюється на правильну числову рівність.

Означення 2. Система (1) називається сумісною, якщо вона має принаймні один розв’язок. Якщо ж система не має жодного розв’язку, вона називається несумісною.

Сумісні системи підрозділяються також на визначені і невизначені.

Означення 3. Сумісна система називається визначеною, якщо вона має лише один розв’язок. В іншому разі сумісна система називається невизначеною.

Основні задачі теорії лінійних рівнянь такі:

1. Дослідити систему на сумісність.

2. Сумісну систему дослідити на визначеність і невизначеність.

3. Дати алгоритми розв’язування.

Суть розв’язування систем рівнянь полягає в тому, щоб звести всі рівняння до рівнянь вигляду:

(2)

або до розв’язування одного рівняння з декількома невідомими з подальшим розв’язуванням рівнянь виду (2).

Інструментом розв’язування системи є елементарні перетворення.

Означення 4. Елементарними перетвореннями системи (1):

1. перестановка двох рівнянь;

2. множення обох частин деякого рівняння на число, не рівне 0;

3. додавання до одного з рівнянь іншого рівняння, в подумках помноженого на деяке число.

Означення 5.Дві системи вигляду (1) з однаковою кількістю невідомих називаються еквівалентними, якщо вони або обидві несумісні, або, у разі сумісності, мають однакові розв’язки.

Для самостійного доведення сформулюємо теорему:

Теорема. Елементарні перетворення приводять до еквівалентних систем.

Перейдемо до дослідження системи (1)лінійних алгебраїчних рівнянь методом Гаусса.

Вважатимемо, що . Якщо це не так, цього можна досягти за рахунок або перестановки рівнянь, або за рахунок перенумерації невідомих. Зробимо такі елементарні перетворення над системою (1):

до рівняння + -ше рівняння

до рівняння + -ше рівняння

………………………………………….

до S рівняння + -ше рівняння

У результаті цих перетворень отримаємо еквівалентну систему

Зауваження. Могло трапитись, що у системі з’явилося рівняння:

(3)

У цьому випадку система , а тому і еквівалентна до неї, несумісна.

Могло трапитись і таке:

(4)

Це рівняння можна задовольнити будь-яким набором чисел. Тому його можна викинути з системи.

У системі вважатимемо, що . Цього можна досягти за рахунок або перестановки рівнянь, або за рахунок перенумерації невідомих. Зробимо такі елементарні перетворення над системою :

до -го рівняння + -ге рівняння

………………………………………….

до -го рівняння + -ге рівняння

Тоді отримаємо таку еквівалентну систему:

Продовжуючи аналогічним чином,на останньому кроці отримаємо систему:

Формально треба дослідити три випадки:

1. 

У цьому випадку в останньому рівнянні невідомі оголосимо вільними у тому сенсі, що їм можна надавати будь-які значення. Тоді з останнього рівняння знайдемо, отже передостаннє рівняння і всі інші послідовно стають рівняннями виду (2). У цьому випадку система має безліч розв’язків, тобто невизначена.

2)

Система набуває вигляду:

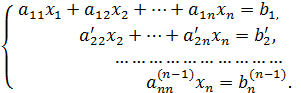
Звідси

У цьому випадку на кожному кроці послідовно отримаємо рівняння вигляду (2). Математики кажуть, що систему зведено до трикутного вигляду. Система є визначеною.

1. 

Легко показати, що це неможливо. Припустимо супротивне , наприклад .Тоді останнє рівняння стає таким:

Ми отримали систему нееквівалентну початковій, що суперечить попередній теоремі.

Отже, метод Гаусса вирішує основні задачі в теорії лінійних рівнянь:

1. Дослідження системи на сумісність. Система буде несумісною, якщо в процесі перетворень ми отримаємо рівняння, в якому коефіцієнти при всіх невідомих рівні нулю, а вільний член - відмінний від нуля. Якщо ж ми такого рівняння не зустрінемо, то система буде сумісною.

2. Сумісна система рівнянь буде визначеною, якщо вона зводиться до трикутного вигляду, і невизначеною, якщо зводиться до вигляду , ().

3. Отримано алгоритм розв’язування системи алгебраїчних рівнянь методом послідовного виключення невідомих (метод Гаусса), поданий вище.