
Хвостенко Кривые 2 порядка
.pdf
|
К Р И В Ы Е В Т О Р О Г О П О Р Я Д К А |
|
|
|
|||||||
|
О к р у ж н о с т ь |
|
|
|
|
||||||
|
Окружностью называется геометрическое место точек плоскости, равно- |
||||||||||
удалённых от данной точки, называемой центром. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
Пусть C a, b |
– центр окружности. |
||
y |
M1 |
|
|
|
|
|
|
Расстояние от любой точки окружности до |
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
M 2 |
центра r – радиус окружности. M x, y – |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
любая точка окружности (рис. 1). |
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
r |
|
|
|
r x a 2 y b 2 , |
||||
|
|
|
|
|
|
|
|
|
|
||
|
M |
|
|
|
|
x a 2 y b 2 r2 |
(1) |
||||
O |
|
|
|
|
|
x |
Уравнение (1) есть уравнение окруж- |
||||
|
|
|
Рис. 1 |
|
ности с центром C a, b и радиусом r . |
||||||
|
|
|
|
|
|
|
|
||||
|
Если M |
1 |
x , |
y |
лежит вне окружности, то x a 2 |
y b 2 |
r2 . |
|
|||
|
|
1 |
|
1 |
|
1 |
1 |
|
|
||
|
Если M |
2 |
x |
, y |
2 |
лежит внутри окружности, то x a 2 y |
b 2 |
r2 . |
|||
|
|
2 |
|
|
|
2 |
2 |
|
|
||
|
Если центр окружности лежит в начале координат, то уравнение (1) имеет |
||||||||||
вид:
x2 y2 r2 . |
(2) |
Уравнение (2) есть каноническое уравнение окружности. Параметриче- |
|
ские уравнения окружности x x0 r cost , |
y y0 r sin t , где x0 , y0 – коорди- |
наты центра окружности, 0 t 2 . |
|
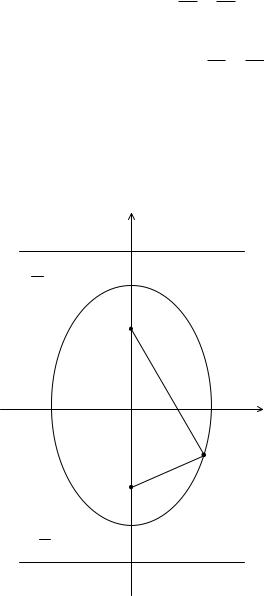
Э л л и п с
Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назы-
ваемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами (рис. 2, 3).
|
a |
|
|
a b |
|
|
y |
|
|
|
|
a |
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
b |
B |
M |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
r1 |
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
F2 |
A |
|
|
|
||
|
|
|
|
a |
c |
|
|
|
O |
c |
a |
|
x |
|||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2. |
|
|
|
|
|
||
Каноническое уравнение эллипса имеет вид: |
|
|
|
|
||||||||||||
|
|
|
|
|
|
x2 |
|
|
y2 |
1. |
|
(3) |
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a OA – большая полуось, b OM – малая полуось. Центр в начале координат.
Фокусы F c; 0 и F c; 0 , где c |
|
a b , c |
|
|
|
a b . |
||||||||||||||
a2 b2 |
b2 a2 |
|||||||||||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эксцентриситетом эллипса называется отношение фокусного расстоя- |
||||||||||||||||||||
ния 2c к длине 2a большой оси. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2c |
|
c |
, 1 |
b2 |
|
a b , |
|
2c |
|
c |
, 1 |
a2 |
|
a b . |
|||||
|
|
a2 |
|
|
|
|
||||||||||||||
|
2a |
|
a |
|
|
|
|
|
|
2b |
|
b |
|
|
|
b2 |
||||
Чем больше , тем более эллипс вытянут вдоль большой оси, чем меньше
, тем более эллипс по форме ближе к окружности.
0 .
Фокальными радиусами точки M эллипса называются отрезки прямых,
соединяющих эту точку с фокусами F1 и F2 . Их длины r1 |
и r2 |
вычисляются по |
|||||||||||||||||
формулам r1 a x , r2 a x , r1 r2 |
2a , где |
– эксцентриситет эллипса. |
|||||||||||||||||
|
Директрисами эллипса называются прямые, определяемые уравнениями |
||||||||||||||||||
x |
a |
, |
x |
a |
|
a b , y |
b |
, |
y |
b |
|
a b . |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Если a b , то эллипс превращается в окружность x2 |
y 2 |
a2 . |
||||||||||||||||
|
Если M |
|
x , y лежит на эллипсе, то |
x12 |
|
y12 |
1. |
|
|
||||||||||
|
1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если M |
x , y лежит вне эллипса, то x12 |
y12 |
1. |
|
||||||||
1 |
1 |
1 |
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если M |
x , y лежит внутри эллипса, то x12 |
y12 |
1. |
|
||||||||
1 |
1 |
1 |
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если центр эллипса перемещен в точку x0 , |
y0 , |
то каноническое уравне- |
||||||||||
ние эллипса примет вид |
x x0 2 |
|
y y0 |
2 |
|
|
|
|
|
|||
a2 |
|
b2 |
1. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y |
|
|
a b |
|
|
||
|
|
|
a |
|
b |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F c |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
a |
|
|
O |
|
a |
|
x |
|
|
|
|
|
|
|
|
|
r2 |
M |
|
|
|
|
|
|
|
|
|
F2 |
c |
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3. |
|
|
|
|
|
||
Параметри- |
|
|
|
|
|
|
|
|
|
ческие |
уравнения эл- |
|
липса имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
x a cost , y bsin t , 0 t 2 .
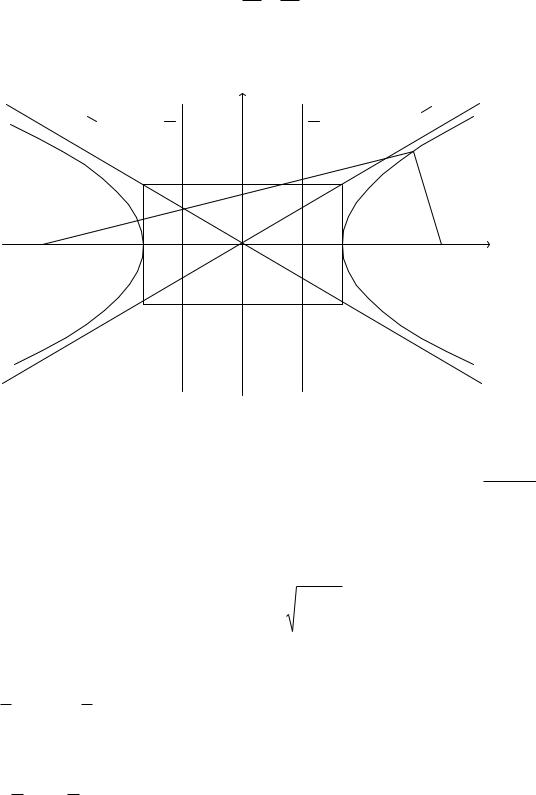
Г и п е р б о л а
Гиперболой называется геометрическое место точек плоскости, для каж-
дой из которых модуль разности расстояний до двух данных точек, называемых фокусами, той же плоскости есть величина постоянная.
Каноническое уравнение гиперболы (рис. 4) имеет вид:
|
|
|
|
x2 |
y2 |
1, |
|
|
|
|
|
|
a2 |
b2 |
|
|
|
где a OA – действительная полуось, b OB – мнимая полуось. |
|
|||||||
|
b |
|
|
y |
|
|
|
|
|
|
a |
|
a |
|
|
||
|
|
|
|
|
|
|
||
a |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
M |
|
|
|
|
|
b B |
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
F1 |
r1 |
|
A' |
|
|
A |
F2 |
|
|
|
|
|
|
||||
c |
|
a |
|
O |
|
a |
c |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
b B' |
|
|
|
|
Рис. 4.
Центр лежит в начале координат. A и A' – вершины гиперболы.
Координаты фокусов гиперболы F1 c; 0 и F2 c; 0 , где c 
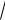 a2 b2 .
a2 b2 .
Эксцентриситетом гиперболы называется отношение фокусного расстоя-
ния 2c к длине 2a действительной оси.
|
c |
, 1 |
b2 |
1. |
|
a |
a2 |
||||
|
|
|
Асимптотами гиперболы называются прямые, определяемые уравнения-
ми y ba x , y ba x .
Директрисами гиперболы называются прямее, определяемые уравнения-
ми x a , x a .
Фокальные радиусы точки правой ветви гиперболы вычисляются по фор-
мулам r1 x a , r2 x a .
Фокальные радиусы точки левой ветви гиперболы вычисляются по фор- |
||||||
мулам r1 x a , r2 x a . |
|
|
|
|
|
|
Для любой точки M гиперболы выполняется условие F1M F2 M 2a . |
||||||
Если центр гиперболы смещен параллельно относительно системы коор- |
||||||
динат xOy таким образом, что центр гиперболы находится в точке C x0 ; y0 , то- |
||||||
гда гипербола определяется уравнением |
|
|
|
|
||
x x0 |
2 |
y y0 |
2 |
|
|
|
|
a2 |
|
b2 |
1. |
|
|
|
|
|
|
|
||
Гипербола (рис. 5), уравнение которой имеет вид x2 |
y2 1, называет- |
|||||
|
|
|
|
|
a2 |
b2 |
ся сопряженной с гиперболой x2 |
y2 |
1. |
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
c |
F2 |
|
b |
|
|
|
|
|
|
a |
|
|
|
|
r2 |
|
|
||
|
|
|
|
|
||
|
|
B |
|
b |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A' |
|
|
A |
|
|
|
a |
|
O |
a |
|
x |
|
|
b |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 |
M |
|
|
|
|
|
|
|
|
|
|
c |
F |
|
|
|
|
|
|
1 |
|
|
|
|
|
Рис. 5. |
|
|
|
|
|

BB' – вершины гиперболы.
b OB – действительная полуось, a OA – мнимая полуось.
Фокусы F 0; c и |
|
|
0; c , где c |
|
|
|
|
|||||||||||
F |
a2 |
b2 . |
|
|||||||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Асимптоты y |
b |
x , |
y |
b |
x . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
a |
|
|
|
|
a |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Эксцентриситет |
c |
, |
a2 |
|
1. |
|
|
|
||||||||||
b |
b2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Директрисы y |
b |
, |
y |
b |
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Фокальные радиусы верхней ветви гиперболы r1 |
y b , r2 y b . |
|||||||||||||||||
Фокальные радиусы нижней ветви гиперболы r1 |
y b , r2 y b . |
|||||||||||||||||
П а р а б о л а
Параболой называется геометрическое место точек, для каждой из кото-
рых расстояние до данной точки, называемой фокусом, равно расстоянию до данной прямой, называемой директрисой.
|
|
y |
|
|
|
p |
N |
|
M |
Уравнение параболы (рис. 6), симмет- |
|
|
|
|
|||
2 |
|
|
|
ричной относительно оси Ox и проходящей |
|
|
|
r |
|
||
|
|
|
через начало координат, имеет вид: |
||
|
|
|
|
||
|
O |
F |
|
x |
y2 2 px . |
|
|
|
|
Уравнение директрисы x p . |
|
|
|
|
|
|
2 |
|
|
|
|
p |
|
|
|
|
|
Фокус F |
; 0 . Фокальный радиус от |
|
|
Рис. 6. |
|
2 |
|
|
|
|
|
|
|
M x; y вычисляется по формуле r x 2p .
Для любой точки M параболы выполняется правило MF MN . p 0 – параметр параболы.
|
Если вершина параболы находится в точке C x0 , y0 , то параболы опреде- |
|||||||
ляется уравнением y y0 2 2 p x x0 . |
|
|
|
|
||||
|
Эксцентриситет параболы равен единицы. |
|
|
|
|
|||
|
Если |
фокус |
параболы имеет координаты |
|
y |
|
|
|
|
p |
|
|
|
|
M |
|
N |
|
|
|
|
|
||||
F |
|
; 0 , уравнение параболы (рис. 7) имеет |
|
|
|
|
||
|
2 |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
вид: |
y2 2 px . |
|
|
|
|
|
||
|
Если фокус параболы лежит на оси Oy в |
|
F |
O |
x |
|||
|
|
|
|
|||||
|
|
|
p |
|
|
|
|
p |
точке |
|
|
|
|
2 |
|||
F 0; |
, то уравнение параболы (рис. 8) |
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
имеет вид: |
x2 2 py . |
|
|
|
|
|||
|
|
|
|
|
|
Рис. 7. |
|
|
|
|
|
|
|
|
p |
|
|
|
Если фокус параболы лежит в точке F 0; |
, то уравнение параболы |
||||||
|
|
|
|
|
|
2 |
|
|
(рис. 9) имеет вид: x2 2 py . |
|
|
|
|
||||
|
|
|
y |
p |
|
y |
|
|
|
|
|
|
|
|
|
||
|
N |
|
|
2 |
|
F |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
x |
|
|
M |
|
|
|
|
|
|
|
|
||
M |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
O |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
F |
p |
|
N |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Рис. 8. |
|
|
Рис. 9. |
|
|
|
|
|
|
|
|
|
|
||
