WinRAR archive_1 / ст / Statistika

Средние величины – используются для компенсации случайных отклонений индивидуальных значений.

Средняя арифметическая:

простая средняя арифметическая

,

где – значение признака – варианты;

– общее число значений – объем совокупности.

взвешенная средняя (для совпадающих значений признака)

,

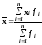где - число совпадений на уровне – частота варианты.

Средняя гармоническая:

простая средняя гармоническая

или ,

взвешенная средняя гармоническая

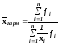или .

Средняя геометрическая .

Модой называется варианта с наибольшей частотой (дискретный ряд).

Для интервального ряда

,

где – величина интервала, - начало модального интервала, - частоты модального, предыдущего и последующего интервалов соответственно.

Мода может быть найдена графически по гистограмме.

Медианой называется варианта, стоящая в середине ряда распределения.

Для дискретного ряда:

если ;если .

Для интервального ряда:

,

где - начало медианного интервала,

- частота медианного интервала,

– величина интервала,

– объем совокупности.

- накопленная частота (до медианного интервала).

Среднее линейное отклонение

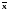, где - варианты, - средняя арифметическая,

или

, где - отклонения вариант от среднего.

После группировок: .

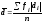Дисперсия

- для первичного дискретного ряда;

- после группировок.

Дисперсия есть мера разброса, рассеяния вариант относительно среднего .

Дисперсия может рассчитываться по формуле:

, где - среднее из квадратов вариант.

Среднее квадратическое отклонение

- мера рассеяния с размерностью вариант _.

Исправленная дисперсия,

Исправленное среднеквадратическое отклонение

.

Коэффициент вариации .

Показатели формы распределения – асимметрия и эксцесс – являются количественными показателями отклонения полигона частот (гистограммы) от графика плотности нормального распределения (кривой Гаусса).

Асимметрия , или .

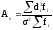Эксцесс .

Важнейшее условие составления рядов динамики – сопоставимость статистических данных.

Средняя хронологическая (временная)

Для моментного ряда: , где – уровни ряда.

Для интервального ряда: .

Темпы динамики

- базисные, - цепные.

Выражаются в виде коэффициентов или процентов.

Прирост (абсолютный)

- базисный, - цепной.

Темпы прироста

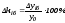- базисные, - цепные.

Средний абсолютный прирост или .

Средний темп динамики .

Средний темп прироста .

Средняя ошибка: для повторной выборки - ;

для бесповторной выборки - ,

где, – средняя из дисперсий групп (групповых дисперсий).

Серийная выборка: проводится случайный отбор групп (серий). Внутри каждой отобранной группы проводится сплошное наблюдение.

Межгрупповая (межсерийная) дисперсия

,

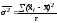где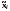 - средняя серии;

- общая средняя;

- число серий.

Средняя ошибка (для равновеликих серий)

- для повторной выборки;

- для бесповторной выборки,

где - число серий (групп) в генеральной совокупности.

Если даны несгруппированные данные в виде двойной выборки

X			…
Y			…

(без повторений значений ), то методом наименьших квадратов можно построить уравнение регрессии . Параметры и находятся из следующей системы нормальных уравнений:

Коэффициент называется коэффициентом регрессии на и характеризует скорость изменения регрессии в зависимости от изменения . Существенно зависит от масштаба измерения.

Параметры уравнения линейной регрессии могут быть найдены по формулам:

, ,

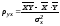где - средние и ;

- среднее из произведений;

- дисперсия X.

Коэффициентом корреляции двух признаков называется величина

или .