4.7. Прогноз залежної змінної.

Економетричне моделювання зв’язку між економічними показ­никами завжди складаєтьмя з трьох етапів: побудови економетричної моделі;перевірки статистичної значущості моделі та оцінювання її параметрів; прогнозування на основі моделі. Використаємо модель (4.1) для знаходження прогнозного значення y₀, яке відповідатиме очікуваним значенням матриці незалежних змінних X₀.

Розглянемо спочатку точковий прогноз і припустимо, що ми визначили його як деяку лінійну функцію від y_i:

(4.20)

де і — номер спостереження ();— вагові коефіцієнти значень(їх потрібно вибрати так, щоб значеннябуло найкращим лінійним незміщеним прогнозом).

Оскільки то незміщена точкова оцінка прогнозу

(4.21)

де Х₀ — матриця очікуваних значень пояснювальних змінних.

Задаючи X₀, підставимо значення цього вектора в побудовану економетричну модель

(4.22)

Щоб дістати інтервальний прогноз, необхідно розрахувати середню похибку прогнозу.

Вона зростає з віддаленням прогнозного значення від відповідного середнього значення вибірки.

Розрахуємо спочатку дисперсію прогнозу.

У матричному вигляді дисперсія похибки прогнозу подається так:

. (4.23)

Середньоквадратична похибка прогнозу

(4.24)

Довірчий інтервал для прогнозних значень

(4.25)

де t_ — критичне значення t-критерію при n – m ступенях свободи і рівні значущості .

Зауважимо, що є точковою оцінкою як математичного сподівання прогнозного значення, так і його індивідуального значеннядля відповідних незалежних змінних, що лежить за межами базового періоду.

Для визначення інтервального прогнозу індивідуального значення необхідно знайти відповідну стандартну похибку:

Отже, інтервальний прогноз індивідуального значення визначається як

або

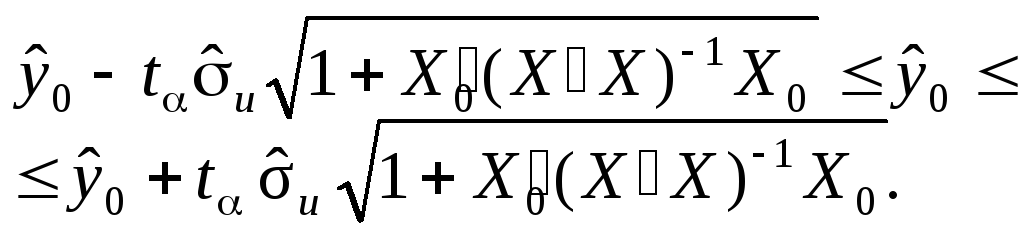
Приклад 4.4. Необхідно розрахувати для економетричної моделі (приклад 4.1) точковий та інтервальний прогнози математичого сподівання та індивідуального значення залежної змінної, коли для прогнозного періоду заданий вектор

.

Розв’язання. 1.  Визначимо точкові прогнозні значення залежної змінної, коли

: то .

Отже, y₀ можна інтерпретувати як точкову оцінку прогнозного значення математичного сподівання та індивідуального значення витрат на харчування, коли відомі загальні витрати x₁ = 500 і розмір сім’ї становить x₂ = 6.

2. Визначаємо прогнозний інтервал математичного сподівання :

Стандартна похибка прогнозу математичного сподівання

.

3. Знайдемо інтервальний прогноз для . При цьому нехай = 0,05 і n – m = 13; тоді t_0,05 = 2,160.

Отже,

і

150,62 – 2,160  21,95 150,62 + 2,160 21,95;

150,62 – 47,412 150,62 + 47,412;

103,208 198,032.

4. Обчислимо дисперсію і стандартну похибку прогнозу індивідуального значення :

.

Стандартна похибка прогнозу індивідуального значення y₀ така:

.

5. Визначимо інтервальний прогноз індивідуального значення y₀:

;

150,62 – 2,160  23,467 150,62 + 2,160 23,467;

150,62 – 50,689 150,62 + 50,689;

99,931 201,309.

Значення t_ знаходимо в таблиці при  = 0,05 і ступені свободи  = 13. У такому разі t_0,05 = 2,160.

Отже, з імовірністю р = 0,95 ( = 0,05) прогноз математичного сподівання М(y₀) потрапляє в інтервал [103,208; 198,032], а прогноз індивідуального значення — в інтервал [99,931; 201,309].

Можна також сказати, що з імовірністю р = 0,95 знайдені прогнози покривають М(y₀) і y₀, коли взяти досить велику кількість вибірок і для кожної з них обчислити інтервальні прогнози.

Економічна інтерпретація: якщо у прогнозному періоді загальні витрати мають рівень 500 одиниць, а сім’я складається з шести осіб, то середні витрати на харчування потрапляють в інтервал

103,208 198,032.

Водночас окреме (індивідуальне) значення цих витрат міститиметься в ширшому інтервалі:

99,931 201,309.