4.6. Коваріаційна матриця оцінок параметрів моделі

За допомогою коваріаційної матриці розраховуються основні показники випадкового розсіювання оцінок навколовідповідних істинних значень параметрів, що аналізуються, а також харак­теристики взаємозв’язків отриманих оцінок.

У класичній регресійній моделі Y = XA + u; вектор і залежний від нього векторє випадковими змінними. До оператора оцінюваннявходить вектор , а отже, оператортакож можна вважати випад­ковою функцією оцінювання параметрів моделі.

Відомо, що для характеристики випадкових змінних поряд із математичним сподіванням застосовуються також дисперсіяі коваріація(j  k). Істинні (справжні) значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріаційну матрицю

. (4.12)

Оцінки коваріаційної матриці використовуються для знаходження стандартних похибок та обчислення довірчих інтервалів оцінок параметрів. Вони використовуються й під час перевірки їхньої статистичної значущості.

На головній діагоналі матриці містяться оцінки диспер­сій j-ї оцінки параметрів, що ж до елементів (j  k), які розміщені поза головною діагоналлю, то вони є оцінками коваріації між і

Отже,

, (4.13)

де — незміщена оцінка дисперсії залишків;.

Зауважимо, що матриця коваріації оцінок параметрів моделі характеризує також ступінь їх випадкового розсіювання, який обчислюється, як значення детермінанта коваріаційної матриці cov(A).

Детермінант коваріаційної матриці є так званоюузагальненою дисперсією, яка кількісно характеризує ступінь випадкового розсіювання значень векторної випадкової величини навколо свого середнього у відповідному багатовимірному просторі:

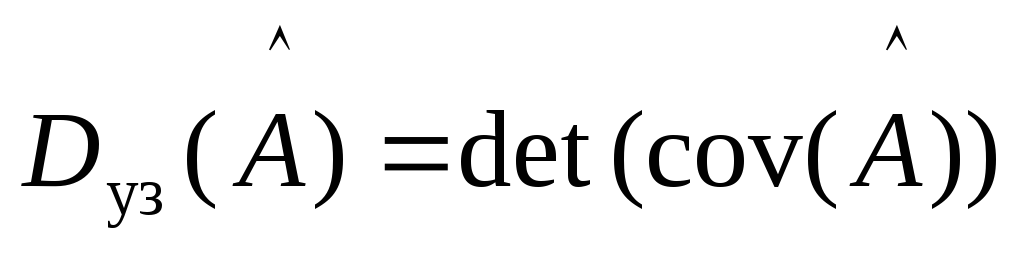. (4.14)

Часто використовується й інша характеристика цього випадкового розсіювання значень багатовимірної випадкової величини — слід коваріаційної матриці tr:

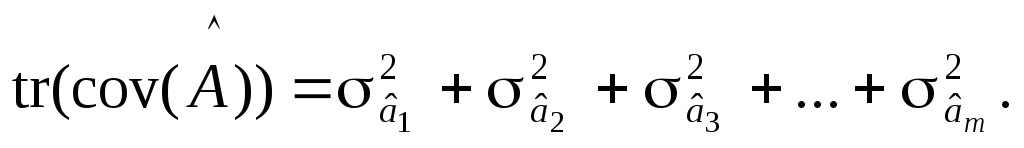(4.15)

Виходячи із додатної визначеності матриці і змісту діагональних елементів , можна стверджувати, що величини, які визначені співвідношеннями (4.14) і (4.15), завжди додатні. Чим більше значення знайдених характеристик (детермінанта, сліду дисперсійно-кореляційної матриці), тим більша загальна варіація оцінок параметрів моделі).

Ступінь тісноти взаємозв’язку між окремими оцінками параметрів моделі івекторакраще визначати на основікоефіцієнта кореляції, який, у свою чергу, визначається через елемен­ти коваріаційної матриці :

. (4.16)

Усе це говорить про те, що коваріаційна матриця вектора оцінок параметрів моделей містить досить важливу інформацію про їхню якість.

Незміщена оцінка дисперсії залишків розраховується так:

, (4.17)

де n — кількість спостережень; m — кількість змінних у моделі.

Оскільки вектор залишків , то добуток векторівможна записати так:

Звідси маємо альтернативну форму запису дисперсії залишків:

.

Позначимо (k, j)-й елемент матриці символом, тодіj-й елемент по головній діагоналі матриці обчислюється за формулою:

. (4.18)

Коваріації що містяться за межами головної діагоналі, відповідно такі:

. (4.19)

Приклад 4.3. Для економетричної моделі Y = 8,8 + 0,2Х₁ + + 6,97Х₂ + u, (приклад 4.1) обчислимо коваріаційну матрицю .

Отже, маємо:

; ;

;

n = 16; m = 2.

Розв’язання. 1. Обчислимо незміщену оцінку дисперсії залишків , скориставшись співвідношенням:

;

;

.

2. Визначимо дисперсії оцінок :

= 68,92  0,314 = 21,64;

= 68,92  0,00003 = 0,00207;

= 68,92  0,0165 = 1,137.

3. Обчислимо коваріації відповідних оцінок параметрів:

= 68,92  (–0,00017) = –0,0118;

= 68,92  (–0,0446) = –3,0738;

= 68,92  (–0,00012) = –0,00827.

Знак «мінус» перед оцінками коваріацій указує на те, що зі збільшенням однієї оцінки параметрів інша зменшується в середньому і навпаки.

Отже, дістанемо дисперсійно-коваріаційну матрицю

.

4. Запишемо стандартні похибки оцінок параметрів моделі:

;

;

;

.

Стандартні похибки характеризують середні лінійні коливання оцінок параметрів моделі навколо свого математичного сподівання. Чим менші ці похибки, тим стійкіші оцінки параметрів моделі. Остаточні висновки стосовно стійкості оцінок можна зробити лише тоді, коли порівняти її з абсолютними значеннями оцінок параметрів моделі.

Порівняємо кожну стандартну похибку з відповідним числовим значенням оцінки параметра, тобто знайдемо відношення:

;

;

.

Отже, стандартні похибки оцінок параметрів щодо рівня самих оцінок становлять відповідно 52,8 %, 23 % і 15 %, а це свідчить про зміщеність оцінок.

Це означає, що залишки можуть мати систематичну складову, яка зумовлюється неточною специфікацією моделі. Наприклад, не всі основні чинники, що впливають на тижневі витрати, пов’язані з харчуванням (скажімо, ціни на продукти харчування) внесено до моделі.