4.5. Властивості оцінок параметрів

Оцінки параметрів є вибірковими характеристиками, що мають такі властивості:

1) незміщеності; 3) ефективності;

2) обґрунтованості; 4) інваріантності.

Означення 4.2. Вибіркова оцінка параметра А називаєтьсянезміщеною, якщо вона задовольняє рівність

. (4.8)

Застосовуючи оператор математичного сподівання до (4.7), дістаємо:

Оскільки за першою умовою , то. Отже, оцінка параметрів 1МНК єнезміщеною.

Незміщеність — це мінімальна вимога, яка ставиться до оцінок параметрів . Якщо оцінка незміщена, то за багаторазового повторення випадкової вибірки навіть тоді, коли для окремих вибірок, можливо, оцінки були з похибкою, середнє значення цих похибок дорівнює нулю.

Різниця між математичним сподіванням оцінки і значенням оціненого параметра

(4.9)

називається зміщенням оцінки.

Не можна плутати похибку оцінки з її зміщенням. Похибка дорівнює і є випадковою величиною, а зміщення — величина стала.

Другою важливою властивістю оцінки є її обґрунтованість.

Означення 4.3. Вибіркова оцінка параметрів А називаєтьсяобґрунтованою, якщо для довільного справджується співвідношення

(4.10)

Іншими словами, оцінка обґрунтована, коли вона базується на законі великих чисел. Обґрунтованість оцінки означає, що чим більші будуються вибірки, тим більша ймовірність того, що похибка оцінки не перевищуватиме достатньо малого значення .

Для обґрунтованості оцінок, здобутих на основі 1МНК за умови, що Х детермінована, має виконуватися співвідношення:

де Q — додатно визначена матриця.

Третя властивість оцінок Â — ефективність — пов’язана зі значенням дисперсії оцінок.

Тут доречно сформулювати важливу теорему Гаусса—Маркова, що стосується ефективності оцінки 1МНК.

 Теорема Гаусса—Маркова. Функція оцінювання за методом 1МНК покомпонентно мінімізує дисперсію всіх лінійних незміщених функцій вектора оцінок :

де — дисперсія оцінок, визначених згідно з 1МНК;— дисперсія оцінок, визначених іншими методами.

Отже, функція оцінювання 1МНК у класичній лінійній моделі є найкращою (мінімально дисперсійною) лінійною незміщеною функцією оцінювання. (Цю властивість називають BLUE.)

З означення дисперсії випливає, що — параметр розподілу випадкової величиниÂ, яка є мірою розсіювання її значень навколо математичного сподівання.

Приклад 4.2. Визначити кількісну залежність між прибутком фірми і основними видами ресурсів, які вона вкладає у свою господарську діяльність:

• інвестиції;

• основні виробничі фонди;

• фонд робочого часу.

Для побудови економетричної моделі використаємо статистич­ну інформацію, що наведена в табл. 4.2.

Таблиця 4.2

Місяць	Прибуток Y, гр. од.	Інвестиції Х1, гр. од.	ОВФ Х2, гр. од.	ФРЧ Х3, людино–днів
1	39	62	22	104
2	41	65	25	109
3	38	57	17	99
4	42	66	27	114
5	44	69	28	116
6	49	58	20	110
7	44	72	32	119
8	45	70	30	116
9	48	75	34	114
10	51	79	35	120
11	49	77	33	124
12	54	82	37	119
13	55	80	37	129
14	57	75	39	129
15	56	83	38	132
16	54	81	36	130
17	59	87	40	124
18	61	92	42	134
19	62	95	43	137
20	64	97	42	139

1. Ідентифікуємо змінні моделі.

Y — вектор прибутку, залежна або пояснювана змінна;

X₁ — вектор інвестицій (незалежна або пояснювальна змінна);

X₂ — вектор основних виробничих фондів, незалежна або пояснювальна змінна;

X₃ — вектор фонду робочого часу (незалежна або пояснювальна змінна).

2. Специфікуємо економетричну модель.

У лінійній формі:

Y = a₀ + a₁X₁ +a₂X₂ + a₃X₃ + u;

у степеневій формі:

.

У цих функціях a_j, — параметри економетричної моделі;

u — стохастична або випадкова складова, яка визначає вплив усіх випадкових чинників на прибуток.

Подамо степеневу функцію в лінійно-логарифмічній формі:

LnY = lna₀ + a₁lnX₁ + a₂lnX₂ + a₃lnX₃ + lnu.

Запишемо розрахункові економетричні моделі на основі заданої статистичної інформації:

,

.

У цих розрахункових моделях , — оцінки параметрів моделі за сукупністю спостережень.

Вектор стохастичної складової визначається як різниця між векторами фактичного і розрахункового прибутку залежної змінної (надалі послуговуватимемося терміном «залишки»):

3. Оцінимо параметри цих економетричних моделей методом найменших квадратів, матричний оператор якого

Запишемо матрицю пояснювальних змінних:.

Транспонуємо матрицю Х:

Виконавши множення матриць дістанемо:

.

Знайдемо матрицю, обернену до

.

Помножимо X´Y:.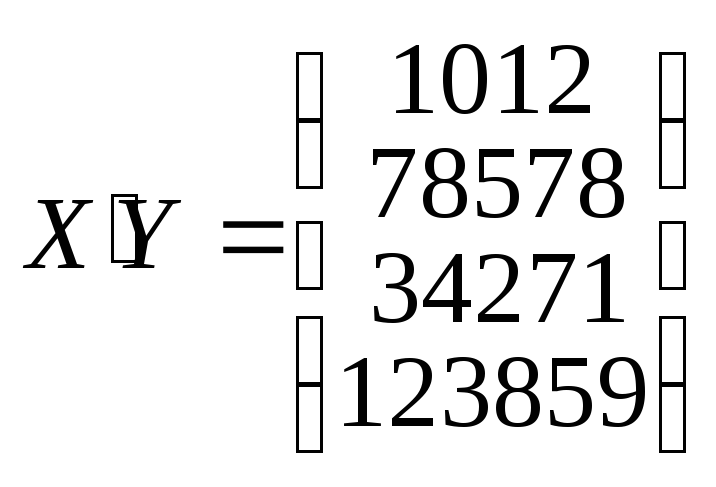

Запишемо вектор :

.

Отже, дістанемо економетричну модель прибутку в лінійній формі:

.

Для побудови степеневої форми моделі прологарифмуємо вихідні дані:

Скориставшись функцією програми «Exсel» «ЛИНЕЙН», знай­демо оцінки параметрів:

0,044037;

0,495475;

–0,10808;

1,099585;

1,045.

Отже, економетрична модель прибутку у степеневій формі набирає вигляду .

Як бачимо, економетрична модель прибутку в лінійній формі відрізняється від моделі у степеневій формі. Ця різниця полягає передусім у тому, що оцінки параметрів в обох моделях мають різний економічний зміст.

У лінійній моделі оцінки параметрів характеризують граничний приріст прибутку залежно від граничного приросту кожного ресурсу на одиницю (коли решта — сталі) і в тих одиницях, в яких вони подаються у вихідній інформації.

У степеневій моделі оцінки параметрів характеризують кількісний зв’язок між прибутком та відповідно кожним ресурсом у відносному (відсотковому) виразі — еластичність. Тому їх потрібно тлумачити так: якщо інвестиції зростуть на 1 %, а основні виробничі фонди і фонд робочого часу не зміняться, то прибуток зросте на 0,495 %; якщо основні виробничі фонди зростуть на 1 %, а решта ресурсів буде сталою, то прибуток зменшиться на 0,108 %; і, нарешті, якщо фонд робочого часу зросте на 1 %, і решта ресурсів буде сталою, то прибуток зросте на 1,1 %.

Зміну напряму взаємозв’язку між прибутком та основними виробничими фондами у степеневій моделі можна пояснити особливостями статистичної інформації (можлива мультиколінеарність, автокореляція, про які йтиметься далі).