Физика - лекции / Механика / 3.Кинематика вращат. движения / Кинематика вращательного движения

Лекция

Кинематика вращательного движения

План

1. Тангенциальное и нормальное ускорение

2. Радиус кривизны траектории

3. Угловая скорость, вектор угла поворота, угловое ускорение

4. Связь линейной и угловой скорости

5. Связь линейных и угловых характеристик

1. Тангенциальное и нормальное ускорение

Две составляющие ускорения: тангенциальное ускорение и нормальное ускорение.

Тангенциальное ускорение направлено по касательной к траектории

Нормальное ускорение направлено по нормали к траектории

Тангенциальное ускорение характеризует изменение скорости по величине. Если скорость по величине не изменяется, то тангенциальная составляющая равна нулю, а нормальная составляющая ускорения равна полному ускорению.

Нормальное ускорение характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории.

В общем случае полное ускорение:

Итак, нормальная составляющая вектора ускорения

Чтобы выяснить свойства нормального ускорения, надо установить, чем определяется , т.е быстрота изменения со временем направления касательной к траектории. Она тем больше (), чем больше искривлена траектория и чем быстрее перемещается частица по траектории.

2. Радиус кривизны траектории

Радиус кривизны – это радиус окружности, которая сливается в данном месте с кривой на бесконечно малом её участке.

3. Угловая скорость, вектор угла поворота, угловое ускорение.

Любой поворот полностью определяется указанием оси вращения и угла поворота Δφ относительно этой оси. Если поворот осуществляется на малый угол Δφ << 2π, то можно ввести понятие вектор угла поворота.

Вектор направлен вдоль оси вращения, т.е. перпендикулярно плоскости, в которой происходит вращение.

Ориентация этого вектора определяется правилом буравчика.

Абсолютное значение вектора равно углу поворота Δφ.

Для того, чтобы величин была вектором, она должна не только направление и абсолютное значение, но и удовлетворять правилу сложения векторов. Это можно показать, что при векторном сложении двух углов поворота правило параллелограмма не выполняется. Оно будет справедливо лишь для малого Δφ << 2π

- неполный вектор.

Угловой скоростью называется вектор , направление которого: определяет ориентацию плоскости вращения и по правилу буравчика направление вращения.

Модуль вектора равен производной от угла поворота по времени:

Угловая скорость, в отличие от угла поворота, является полным вектором.

Вектор может изменяться как за счёт изменения скорости вращения тела вокруг оси (по величине), так и за счёт поворота оси вращения в пространстве (по направлению).

Пусть за

Изменение вектора угловой скорости со временем характеризуется величиной угловое ускорение:

Ускоренное

Замедленное

Модуль углового ускорения измеряется в

Угловое ускорение также как и угловая скорость – псевдовектор.

- псевдовектора, т.к. направление вектора поворота связывается с направлением вращения тела.

4. Связь линейной и угловой скорости

Пусть за малый Δt тело повернулось на Δφ. Пусть точки за

Модуль линейной скорости

Связь векторов линейной и угловой скоростей: положение точки определяется радиусом-вектором , вектор из рисунка определяется как векторное произведение и .

Изменение радиуса-вектора со временем только по направлению называется прецессией.

5. Связь линейных и угловых характеристик
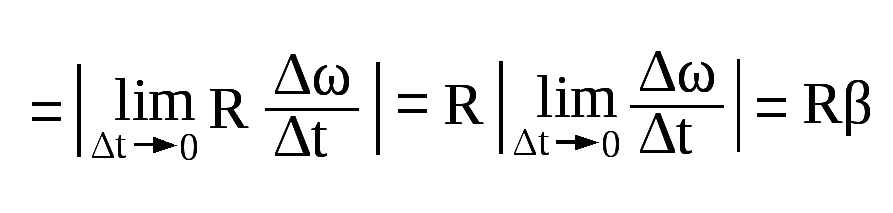