1.15. Энергия электромагнитного поля. Мощность тепловых потерь энергии при протекании токов проводимости. Мощность сторонних источников эмп

Объёмная плотность энергии электрического поля равна

, (1.15.1)

где W_э измеряется в Дж/м³. Столько энергии на единицу объёма нужно затратить, чтобы перевести точку наблюдения Q из состояния (E = 0, D = 0) в состояние (E(Q,t), D(Q,t)).

Объёмная плотность энергии магнитного поля равна

, (1.15.2)

где W_м измеряется в Дж/м³. Столько энергии на единицу объёма нужно затратить, чтобы перевести точку наблюдения Q из состояния (H = 0, B = 0) в состояние (H(Q,t), B(Q,t)).

Объёмная плотность энергии электромагнитного поля равна

. (1.15.3)

В случае линейных электрических и магнитных свойств вещества объёмная плотность энергии ЭМП равна

. (1.15.4)

Это выражение справедливо для мгновенных значений удельной энергии и векторов ЭМП. В случае нелинейных электрических и магнитных свойств вещества эта формула определяет обратимую составляющую энергии на единицу объёма, которую нужно затратить на перевод точки наблюдения Q из состояния отсутствия поля в состояние (E(Q,t), D(Q,t), H(Q,t), B(Q,t)). Если среда обладает гистерезисными магнитными либо диэлектрическими свойствами, то, используя формулы (1.15.1), (1.15.2), (1.15.3), (1.15.4), можно рассчитывать потери энергии на гистерезис при изменении во времени векторов ЭМП.

Удельная мощность тепловых потерь от токов проводимости

Удельная мощность сторонних источников

Единица измерения удельной мощности – Вт/м³.

1.16. Упражнения по энергетическому анализу заданных полей векторов эмп с использованием comsol Script

Задача 1.

Дано. Тетраэдр находится в вакууме. В вершинах тетраэдра заданы значения векторов напряжённости электрического и магнитного поля. Единицы измерения – соответственно В/м и А/м. В объёме тетраэдра эти векторы изменяются по линейному закону. Координаты вершин заданы. Единицы измерения – метры. Узловые распределения векторов заданы так, что их дивергенции равны нулю. Сторонние источники ЭМП в объёме тетраэдра отсутствуют.

Определитьэнергию электрического, магнитного и электромагнитного поля в объёме тетраэдра. Определить мгновенные мощности накопления этих видов энергии в объёме тетраэдра.

Решение.

Зададим узловые распределения векторов случайным образом, как это было сделано в предыдущих задачах. Модифицируем эти распределения функцией otstoiтак, чтобы дивергенции векторных полей были равны нулю. В вакууме=1,=1. Поэтому объёмные плотности энергии электрического и магнитного полей равныW_Э=₀E²/2,W_М=₀H²/2. Если эти плотности проинтегрировать по объёму, то получатся значения энергии. Применив закон электромагнитной индукции и закон полного тока, учитывая, что в вакууме в неподвижной среде могут протекать только токи смещения, получим скорости изменения магнитной индукции и электрического смещения в объёме тетраэдра. Эти скорости распределены в анализируемом объёме равномерно.

E(Q) = [N](Q)[E^(у)];H(Q) = [N](Q)[H^(у)];

Энергия электрического поля вычисляется так:

Энергия магнитного поля:

Мощность накопления энергии электрического поля

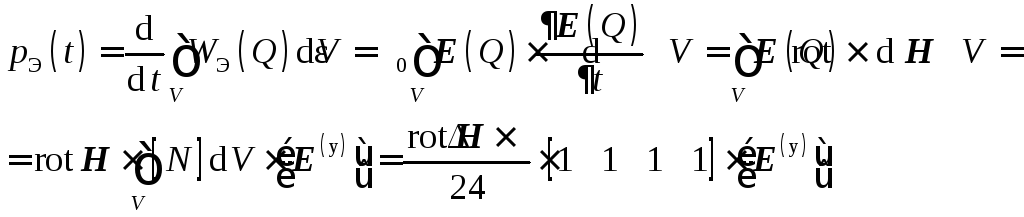
Мощность накопления энергии магнитного поля

Последовательность операторов COMSOLScriptоформим в виде вычислительного сценария. Операторы ввода случайных исходных данных включим в состав этого жеm-файла. Ниже приведён его текст.

% ener_emf - Расчёт энергии ЭМП в объёме тетраэдра

nodes=0.1*rand(4,3) % Координаты узлов тетраэдра, м

E=rand(4,3)*10000-5000; % Значения вектора напряжённости электрического поля в узлах, В/м

H=rand(4,3)*100-50; % Значения вектора напряжённости магнитного поля в узлах, А/м

mu0=4e-7*pi; % Абсолютная магнитная проницаемость вакуума, Гн/м

eps0=8.85419E-12; % Абсолютная диэлектрическая проницаемость вакуума, Ф/м

[grad,div,rote]=grad_div_rot(nodes,ones(4,1),E);

F=otstoi(nodes,E,rote);

E(end,:)=F.' % Теперь div E = 0

[grad,div,roth]=grad_div_rot(nodes,ones(4,1),H);

F=otstoi(nodes,H,roth);

H(end,:)=F.' % Теперь div H = 0

de=abs(det([ones(4,1) nodes])); % Шестикратный объём тетраэдра

ma=eye(4)+ones(4,4);

UE=eps0*de/240*sum(dot(E,ma*E,2)) % Энергия электрического поля, Дж

UM=mu0*de/240*sum(dot(H,ma*H,2)) % Энергия магнитного поля, Дж

U=UE+UM % Энергия ЭМП, Дж

pE=de/24*dot(roth,sum(E)) % Мощность накопления энергии электрического поля, Вт

pM=-de/24*dot(rote,sum(H)) % Мощность накопления энергии магнитного поля, Вт

p=pE+pM % Мощность накопления энергии ЭМП, Вт

Запустим на выполнение этот вычислительный сценарий из командного окна COMSOLScript.

C» ener_emf

nodes =

0.07413565444730 0.05005279194151 0.09243847878884

0.05611883718735 0.02286918125054 7.66452227850e-004

0.07263132412423 0.00636457493582 0.05462130584484

0.08221670829349 0.03643491779045 0.05080149975125

E =

-1.52908951345e+003 -963.59871149687251 4.80954855052e+003

1.56591835268e+003 -737.86015338358902 -2.20352303560e+003

-3.25961623387e+003 3.74984632338e+003 -1.33773865057e+003

24.86219292705629 3.21234053388e+003 -714.82503735431442

H =

-7.38619546130244 20.39294597957436 -10.14124359854716

5.60598467179608 -9.08348106727826 -10.01148967285048

14.02785014707611 -37.59505454442122 -48.88527156440676

-18.41385213235850 28.63320367358517 2.92416295760912

UE =

1.93272875466e-010

UM =

2.59132094912e-009

U =

2.78459382459e-009

pE =

-15.77838954407327

pM =

20.18878606154723

p =

4.41039651747395

Получились следующие результаты расчёта:

энергия электрического поля в объёме тетраэдра равна 1.9327287546610^-10 Дж,

энергия магнитного поля равна 2.5913209491210^-9Дж,

энергия электромагнитного поля равна 2.7845938245910^-9Дж,

мощность накопления энергии электрического поля составила -15.77838954407327 Вт, это означает, что энергия электрического поля в рассматриваемом объёме расходуется в данный момент времени со скоростью 15.77838954407327 Дж/с,

мощность накопления энергии магнитного поля составила 20.18878606154723 Вт, т.е. эта энергия накапливается со скоростью 20.18878606154723 Дж/с,

мощность накопления энергии электромагнитного поля составила 4.41039651747395 Вт, т.е. эта энергия накапливается со скоростью 4.41039651747395 Дж/с.

Задача 2.

Дано. Тетраэдр находится в проводящей среде с заданным значением удельной электрической проводимости. В вершинах тетраэдра заданы значения векторов напряжённости электрического и магнитного поля. Единицы измерения – соответственно В/м и А/м. В объёме тетраэдра эти векторы изменяются по линейному закону. Координаты вершин заданы. Единицы измерения – метры. Узловые распределения векторов заданы так, что их дивергенции равны нулю. Имеются сторонние объёмно-распределённые источники тока в объёме тетраэдра. Составляющие плотности тока не заданы. Токами смещения можно пренебречь. Сторонняя составляющая вектора напряжённости электрического поля равна нулю.

Определитьмощность тепловых потерь в объёме тетраэдра при протекании тока проводимости. Определить электромагнитную мощность, генерируемую объёмно-распределённым источником тока в рассматриваемом объёме.

Решение.

Зададим узловые распределения векторов случайным образом, как это было сделано в предыдущих задачах. Модифицируем эти распределения функцией otstoiтак, чтобы дивергенции векторных полей были равны нулю. Ротор напряжённости магнитного поля равен полной плотности тока. По условиям данной задачи полная плотность тока распределена в объёме тетраэдра равномерно, потому что напряжённость магнитного поля распределена линейно.

Последовательность операторов COMSOLScriptоформим в виде вычислительного сценария. Операторы ввода случайных исходных данных включим в состав этого жеm-файла. Ниже приведён его текст.

% power_cur - Расчёт мощности при протекании тока

nodes=0.1*rand(4,3) % Координаты узлов тетраэдра, м

E=rand(4,3)-0.5; % Значения вектора напряжённости электрического поля в узлах, В/м

H=rand(4,3)*3000-1500; % Значения вектора напряжённости магнитного поля в узлах, А/м

gam=1E6; % Удельная электрическая проводимость вещества внутри тетраэдра, См/м

[grad,div,rote]=grad_div_rot(nodes,ones(4,1),E);

F=otstoi(nodes,E,rote);

E(end,:)=F.' % Теперь div E = 0

[grad,div,roth]=grad_div_rot(nodes,ones(4,1),H);

F=otstoi(nodes,H,roth);

H(end,:)=F.' % Теперь div H = 0

de=abs(det([ones(4,1) nodes])); % Шестикратный объём тетраэдра

ma=eye(4)+ones(4,4);

% roth - полная плотность тока, А/м^2

decon=gam*E; % Узловое распределение плотности тока проводимости

denem=repmat(roth,4,1)-decon; % Сторонняя плотность тока в узлах

pow_heat=de/120*sum(dot(decon,ma*E,2)) % Мощность тепловых потерь, Вт

pow_sour=-de/120*sum(dot(denem,ma*E,2)) % Мощность стороннего источника тока, Вт

Запустим на выполнение этот вычислительный сценарий из командного окна COMSOLScript.

C» power_cur

nodes =

0.01108035733379 0.04561510214864 0.01434380222677

0.07277991320743 0.00270110466597 0.09833856215778

0.00512829600308 0.08162500924789 0.00540263145506

0.01393043253571 0.08798039024878 0.01777575499173

E =

0.03593333685112 -0.36579090912196 0.48494717558657

0.07963264578989 0.40486794562053 -0.03852575546681

-0.21038612148555 -0.36319613070119 -0.06721132364824

0.12724279523511 -0.25821981980774 0.19702265451285

H =

334.35216460951733 895.17427751251580 909.28160366232350

1.31356640445e+003 -706.02311180004358 860.73821591846672

-1.02862618721e+003 622.94620706256819 548.26655980765281

-485.19590732744734 193.58299928398475 1.62641858944e+003

pow_heat =

0.01785692781837

pow_sour =

0.13848507551475

Получились следующие результаты расчёта:

Мощность тепловых потерь при протекании тока проводимости равна 0.01785692781837 Вт,

Генерируемая мощность стороннего источника тока равна 0.13848507551475 Вт.