
- •Теория электромагнитного поля
- •1. Общие вопросы теории электромагнитного поля
- •1.1. Определение электромагнитного поля
- •1.2. Краткая характеристика математического аппарата теории эмп
- •1.3. Определения векторов напряжённости электрического поля и магнитной индукции
- •В соответствии с этим определением электрическая сила, действующая на точечный заряд q равна:
- •1.4. Определения векторов электрического смещения и напряжённости магнитного поля в вакууме
- •1.5. Первичные физические источники эмп
- •1.6. Электрическая поляризованность вещества. Намагниченность вещества
- •1.7. Общие определения векторов электрического смещения и напряжённости магнитного поля
- •1.8. Объёмная плотность заряда. Плотность тока
- •1.9. Упражнения в comsol Script
- •1.10. Уравнения эмп в интегральной форме
- •1.11. Уравнения эмп в дифференциальной форме (уравнения Максвелла) для неподвижных сред
- •1.12. Упражнения по анализу заданных полей векторов эмп с использованием уравнений эмп в дифференциальной форме
- •1.13. Соотношения между векторами поля и электрофизическими свойствами среды
- •Способы глобальной линеаризации уравнений материальной связи
- •1.14. Упражнения по построению графиков электрофизических характеристик материалов по справочным данным с помощью comsol Script
- •1.15. Энергия электромагнитного поля. Мощность тепловых потерь энергии при протекании токов проводимости. Мощность сторонних источников эмп
- •1.16. Упражнения по энергетическому анализу заданных полей векторов эмп с использованием comsol Script
- •1.17. Граничные условия для векторов эмп на поверхностях раздела сред. Понятие о поверхностном роторе и поверхностной дивергенции векторного поля
- •1.18. Закон сохранения заряда в дифференциальной и интегральной форме
- •1.19. Граничные условия для компонентов плотности тока на поверхностях раздела сред
- •1.20. Теорема Умова-Пойнтинга
- •1.21. Упражнения по анализу энергетических потоков в заданных полях векторов эмп с использованием comsol Script и теоремы Умова-Пойнтинга
- •2. Электростатическое поле
- •2.1. Определение электростатического поля
- •2.2. Законы электростатического поля в интегральной и дифференциальной форме. Линеаризованное уравнение материальной связи
- •2.3. Граничные условия для векторов электростатического поля на поверхностях раздела диэлектриков и на поверхностях проводников
- •2.4. Понятие о скалярном электрическом потенциале
- •2.5. Уравнение электростатики относительно скалярного электрического потенциала
- •2.6. Коэффициентная и генеральная формы уравнения электростатики в системе Comsol Multiphysics
- •2.7. Скалярная краевая задача электростатики. Типы граничных условий (гу) на границе расчётной области. Задание гу в системе Comsol Multiphysics
- •Если в расчетной области свободные заряды отсутствуют, то
- •2.8. Технология построения моделей электростатических полей в pde Modes, в электростатических прикладных режимах ядра Comsol Multiphysics и Модуля Электромагнетизма
- •2.8.1. Моделирование в pde Modes (Coefficient Form) Навигатор моделей
- •Режимы и настройки
- •Геометрическое моделирование
- •Физическое моделирование
- •Построение сетки конечных элементов
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •2.8.2. Моделирование в pde Modes (General Form) Навигатор моделей
- •Физическое моделирование
- •Построение сетки конечных элементов
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •2.8.3. Моделирование в электростатическом прикладном режиме ядра comsol Multiphysics Навигатор моделей
- •Режимы и настройки
- •Физическое моделирование
- •Построение сетки конечных элементов
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •2.8.4. Моделирование в электростатическом прикладном режиме Модуля Электромагнетизма Навигатор моделей
- •2.9. Энергия системы заряженных проводников
- •2.10. Технология расчёта энергии электростатического поля в моделях Comsol Multiphysics
- •2.11. Фундаментальное решение скалярного уравнения электростатики. Закон Кулона как следствие этого решения
- •2.12. Поле электрического диполя. Упражнение на составление вычислительного сценария расчёта такого поля в Comsol Script
- •В результате получим
- •Окончательно получим
- •Расчёт и визуализация поля электрического диполя в системе comsol Script
- •2.13. Поле бесконечно длинной заряженной оси
- •2.14. Упражнения по аналитическим расчётам параметров электростатических полей в бесконечно длинных коаксиальных системах проводников
- •2.15. Упражнения по моделированию электростатических полей в коаксиальных системах в comsol Multiphysics
- •Навигатор моделей
- •Режимы и настройки
- •Геометрическое моделирование
- •Физическое моделирование
- •Построение сетки конечных элементов
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •Физическое моделирование
- •Режимы и настройки
- •Навигатор моделей
- •Режимы и настройки
- •Геометрическое моделирование
- •Физическое моделирование
- •Построение сетки конечных элементов
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •Физическое моделирование
- •Постпроцессорная обработка и визуализация
- •Режимы и настройки
- •2.15.3. 2D Modeling в электростатическом прикладном режиме ядра comsol Multiphysics
- •Навигатор моделей
- •Режимы и настройки
- •Физическое моделирование
- •Постпроцессорная обработка и визуализация
- •Физическое моделирование
- •Постпроцессорная обработка и визуализация
- •Постпроцессорная обработка и визуализация
- •2.15.4. 2D Modeling в электростатическом прикладном режиме Модуля Электромагнетизма
- •Навигатор моделей
- •Постпроцессорная обработка и визуализация
- •2.16. Поле системы двух параллельных разноимённо заряженных осей
- •2.17. Поле и ёмкость параллельных цилиндров с несовпадающими осями, находящихся один внутри другого
- •2.18. Упражнения по аналитическому расчёту и моделированию в comsol Multiphysics поля и ёмкости «коаксиального» кабеля со смещённой жилой
- •2.18.1. Моделирование в pde Modes (General Form) Навигатор моделей
- •Режимы и настройки
- •Геометрическое моделирование
- •Физическое моделирование
- •Построение сетки конечных элементов
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •2.18.2. Моделирование в электростатическом прикладном режиме ядра comsol Multiphysics Навигатор моделей
- •Режимы и настройки
- •Физическое моделирование
- •Постпроцессорная обработка и визуализация
- •2.18.3. Моделирование в электростатическом прикладном режиме Модуля Электромагнетизма
- •3.2. Граничные условия для векторов электрического поля постоянного тока в проводящей среде на границах раздела сред
- •3.3. Аналогия между электрическим полем в проводящей среде и электростатическим полем в диэлектрике
- •3.4. Коэффициентная и генеральная формы уравнения математической физики относительно скалярного электрического потенциала. Краевая задача анализа постоянного электрического поля
- •3.5. Технология построения моделей постоянных электрических полей в проводящей среде в pde Modes, в электромагнитных прикладных режимах ядра Comsol Multiphysics и Модуля Электромагнетизма
- •3.5.1. Моделирование в pde Modes (Coefficient Form) Навигатор моделей
- •Режимы и настройки
- •Геометрическое моделирование
- •Физическое моделирование
- •Построение сетки конечных элементов
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •3.5.2. Моделирование в pde Modes (General Form) Навигатор моделей
- •Режимы и настройки
- •Физическое моделирование
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •3.5.3. Моделирование в физическом прикладном режиме ядра comsol Multiphysics Навигатор моделей
- •Режимы и настройки
- •Физическое моделирование
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •3.5.4. Моделирование в физическом прикладном режиме Модуля Электромагнетизма Навигатор моделей
- •3.6. Упражнения по расчётам электрических полей растекания токов заземлителей
- •3.6.1. Упражнения по аналитическим расчётам
- •3.6.2. Моделирование в comsol Multiphysics
- •3.6.2.1. Моделирование в pde Modes (General Form) Навигатор моделей
- •Геометрическое моделирование
- •Физическое моделирование
- •Построение сетки конечных элементов
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •3.6.2.2. Моделирование в физическом прикладном режиме ядра comsol Multiphysics Навигатор моделей
- •Физическое моделирование
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
- •3.6.2.3. Моделирование в физическом прикладном режиме Модуля Электромагнетизма
- •Навигатор моделей
- •Режимы и настройки
- •Вычисление решения
- •Постпроцессорная обработка и визуализация
2.12. Поле электрического диполя. Упражнение на составление вычислительного сценария расчёта такого поля в Comsol Script
На рис. 2.12.1 изображён электрический диполь с электрическим дипольным моментом Pэ. Известно, что
Pэ = qh.

Рис. 2.12.1. Электрический диполь и точка наблюдения
![]()
Если источником электростатического поля является точечный диполь, то
h <<R1,h <<R2,
![]()
В результате получим
![]() (2.12.1)
(2.12.1)
Зная распределение скалярного электрического потенциала, можно определить распределение вектора напряженности электрического поля
![]()
В выражении (2.12.1) от положения точки QзависятRиR, поэтому для определения градиента выражения (2.12.1) можно применить правила дифференцирования из векторного анализа
![]()
![]()
![]()
![]()
![]()
Окончательно получим

или в сферической системе координат
![]() .
.
Можно доказать, что уравнение линий напряженности электрического поля (силовых линий) имеет вид
![]() (2.12.2),
(2.12.2),
где А– параметр семейства линий; уравнение эквипотенциальных линий
![]() (2.12.3),
(2.12.3),
где В– параметр семейства линий потенциала.
Чтобы провести
через некоторую точку линию напряженности
или равнопотенциальную кривую следует
подставить в (2.12.2) или (2.12.3) координаты
этой точки и вычислить значение параметра
АилиВ, соответствующее искомой
кривой. Затем, задаваясь различными
значениями
![]() ,
находят значениеRискомых точек линии.
,
находят значениеRискомых точек линии.
Если построить несколько произвольных равнопотенциальных поверхностей и рассечь их различными меридианными плоскостями, то в каждой такой плоскости получится одна и та же картина линий равного потенциала. Такое поле называют плоскомеридианным. В современной литературе такие поля называют «осесимметричными».
Расчёт и визуализация поля электрического диполя в системе comsol Script
Ниже представлен текст вычислительного сценария COMSOL Script, предназначенного для расчёта названного поля.
% el_dipol - Расчёт и визуализация поля электрического диполя
% Электрический дипольный момент направлен вдоль оси y
% Рассчитывается распределение скалярного электрического потенциала
% и компонентов вектора напряжённости электрического поля
P=1; % y-компонента электрического дипольного момента, пКл*м
eps0=8.85419; % Абсолютная диэлектрическая проницаемость вакуума, пФ/м
[x,y]=meshgrid(0.1:0.01:0.5,0.1:0.01:0.5);
fi=P*y./(4*pi*eps0*(x.^2+y.^2).^1.5);
Ex=3*P*y.*x./(4*pi*eps0*(x.^2+y.^2).^2.5);
Ey=P*(3*y.^2./(x.^2+y.^2)+1)./(x.^2+y.^2).^1.5/(4*pi*eps0);
E=sqrt(Ex.^2+Ey.^2);
figure(1)
contour(x,y,fi,19)
grid on
figure(2)
contour(x,y,Ex,29)
grid on
figure(3)
contour(x,y,Ey,29)
grid on
figure(4)
contour(x,y,E,29)
grid on
Ниже показано содержимое фигур COMSOL Script с изолиниями потенциала и компонентов вектора напряжённости электрического поля (рис. 2.12.2 – 2.12.5).
 Рис.
2.12.2. Изолинии скалярного электрического
потенциала
Рис.
2.12.2. Изолинии скалярного электрического
потенциала
 Рис.
2.12.3. Изолинии горизонтальной составляющей
напряжённости электрического поля
Рис.
2.12.3. Изолинии горизонтальной составляющей
напряжённости электрического поля
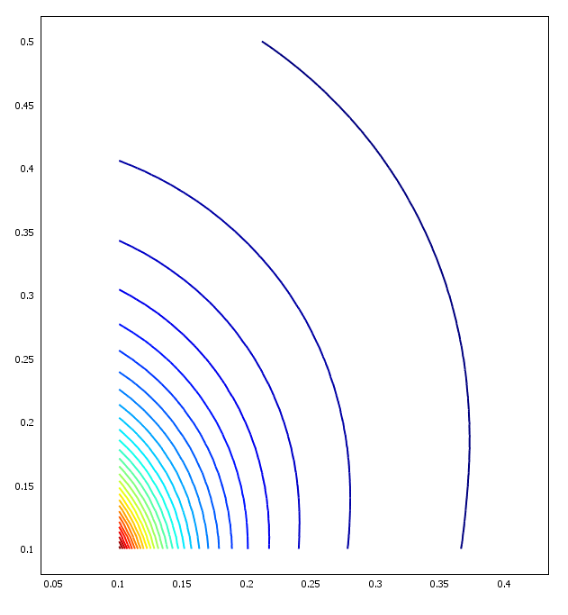 Рис.
2.12.4. Изолинии вертикальной составляющей
напряжённости электрического поля
Рис.
2.12.4. Изолинии вертикальной составляющей
напряжённости электрического поля
 Рис.
2.12.5. Изолинии модуля напряжённости
электрического поля
Рис.
2.12.5. Изолинии модуля напряжённости
электрического поля
2.13. Поле бесконечно длинной заряженной оси
Пусть имеется
бесконечно длинная заряженная ось,
имеющая заряд на единицу длины
![]() (рис. 2.13.1).
(рис. 2.13.1).

Рис. 2.13.1. Бесконечно длинная заряженная ось и след цилиндрической поверхности, проходящей через точку наблюдения
Охватим эту ось цилиндрической поверхностью, ось которой совпадает с заряженной осью. На этой поверхности вектор электрического смещения имеет только нормальную составляющую Dn, причемDn=const. В соответствии с теоремой Гаусса в интегральной форме
![]() ,
,
откуда ![]()
![]()
![]()
![]()
![]()
![]()
Во многих практических случаях электрическое поле можно представить в виде линейной комбинации полей нескольких заряженных осей или нескольких пар разноименно заряженных осей. Поэтому целесообразно рассмотреть поле одной такой пары. Но прежде рассмотрим применение записанных формул для полей в бесконечно длинных коаксиальных системах проводников.
