Лаба 2

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Владимирский государственный университет

Лабораторная работа №2

Определение коэффициентов влияния и расчёт электрических допусков

Выполнил:

студент группы ФОб-107

Чуков Дмитрий Валентинович

Принял:

Талицкий Е. Н.

Владимир 2010

Цель работы: ознакомление с методами определения коэффициентов влияния и расчёта электрических допусков.

Показания, снятые с частомера (), при заданных значениях резистивных и ёмкостных элементов:

R2=9,08 кОм, R3=8,97 кОм, C2=49,9 пФ
C1	F
54,2	1,527
55,1	1,49
53,2	1,517
55,05	1,526
59,35	1,451
55,15	1,52
48	1,608

R3=8,97 кОм, C1=54,2 пФ, C2=49,9 пФ
R2	F
9,08	1,528
8,92	1,543
8,84	1,549
8,99	1,538
8,99	1,537
9,05	1,529

R2=9,08 кОм, C1=54,2 пФ, C2=49,9 пФ
R3	F
8,97	1,528
8,85	1,536
8,85	1,538
9,06	1,519
9,13	1,514
8,97	1,527

R2=9,08 кОм, R3=8,97 кОм, C1=54,2 пФ
C2	F
49,4	1,527
53,2	1,463
50,8	1,504
53,3	1,469
51,5	1,513
55,15	1,463
50,65	1,504

Расчёт коэффициента влияния расчётно-аналитическим методом:

Вычислим частные производные по каждому из параметров:

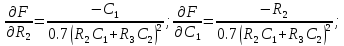
Подставим производные в исходную формулу для нахождения коэффициента влияния и подставим значения параметров:

BR2		BC1		BR3		BC2
-0,526205715		-0,52621		-0,47379		-0,473794285
-0,521771414		-0,53031		-0,47044		-0,492297852
-0,519522991		-0,52156		-0,47044		-0,480766228
-0,523721592		-0,53008		-0,47628		-0,492767231
-0,523721592		-0,54877		-0,4782		-0,484183375
-0,525380558		-0,53054		-0,47379		-0,501296827
		-0,49586				-0,480028083

Вывод по таблице: очевидно, что коэффициент влияния слабо зависит от изменения входных параметров и с приближённой точностью принимает значение, равное 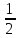во всех случаях. Точное значение коэффициента влияния равно 0,5 так как мультивибратор симметричный и .

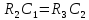Расчёт коэффициента влияния методом малых приращений:

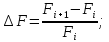
BR2		BC1		BR3		BC2
-0,5571		-1,45922		-0,39136		-0,54486
-0,43357		-0,5255		-0,46642		-0,62121
-0,41851		0,170607		-0,52062		-0,47287
-0,41752		-0,62921		-0,42603		-0,88692
-0,77987		-0,67197		-0,48997		-0,46628
		-0,44656				-0,34346

Есть моменты, когда одному и тому же значению параметра соответствуют разные значения частоты мультивибратора. В этом случае вместо 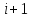значения параметра было взято произвольное значение из таблицы и соответствующее ему значение частоты.

Очевидно, что экспериментальные данные расходятся с теоретическими. Кроме того флуктуации значений при расчётно-аналитическрм методе не значительна: значения приблизительно равно . При методе малых приращений эти значения очень сильно разбросаны (например, максимальное значение получилось ), но большинство значений всё равно приближённо равно .

Расчёт допусков методом предельных отклонений.

Для начала найдём средние значения коэффициентов влияния посчитанных расчётно-аналитическим методом и методом малых приращений:

Расчётно-аналитический метод					Метод малых приращений
BR2	BC1	BR3	BC2	BR2		BC1	BR3	BC2
-0,52338731	-0,52619	-0,47383	-0,486447697	-0,52131		-0,59364	-0,458881474	-0,55593

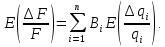
В нашем случае , поэтому .

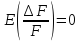Для сопротивления: ; для ёмкости: .

Расчёт допусков вероятностным методом

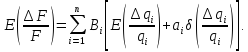
Так как распределение считается нормальным, то , , 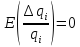откуда .

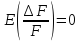Вероятностный метод привёл к тому, что погрешность выходного параметра оказалась меньше чем при методе предельных отклонений.

Значение частоты, рассчитанное по формуле:

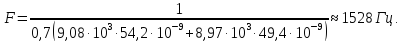
При методе предельных отклонений:

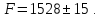
При вероятностном методе:

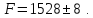
Вывод: в данной работе были посчитаны коэффициенты влияния методами расчётно-аналитическим и малых приращений, а также электрические допуски методами предельных отклонений и вероятностным. Коэффициенты влияния по модулю с приближённой точностью равно 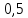, как и должно быть. При расчёте допусков двумя методами были получены два разных значения – и . Получается, что второй метод позволяет найти значение выходного параметра с меньшей погешностью.