
Вопрос 1
.docx|
Вопрос 1:Тепловое излучение(ТИ) – передача энергии от одних тел другим в виде электромагнитных волн за счёт их тепловой энергии. Длинна волны ТИ как у инфракрасного излучения.Характеристики ТИ:- Энергетическая светимость тела – энергия испускаемая телом в единицу времени.- Спектральная плотность энергетической светимости – распределение энергии по всему спектру частот.- Поглощающая способность тела – показывает, какая часть энергии электромагнитного излучения попадающего на тело поглощается телом.- Отражающая способность – показывает, какая часть энергии электромагнитного излучения попадающего на тело отражается телом.- Абсолютно черное тело – модель тела, поглощающая все электромагнитные излучения попадающие на него.- Серое тело – тело, коэффициент поглощения которого зависит только от температуры.Равновесное излучение – тепловое излучение, находящееся в термодинамическом равновесии с веществом.Термодинамическое равновесие – состояние, при котором остаются неизменными по времени макроскопические величины этой системы(к примеру температура) в условии изолированности от окружающей среды. Вопрос 2:Внешний фотоэффект – испускание электронов веществом под действием электромагнитных излучений. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.Основные закономерности:- Закон Столетова: число фотоэлектронов, выбиваемых из катода за 1 с, прямо пропорционально интенсивности излучения.- Максимальная начальная скорость фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой.- Для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света (зависящая от химической природы вещества и состояния поверхности), ниже которой фотоэффект невозможен.Уравнение Эйнштейна: hv = A + (m(vmax)^2)/2v – частота падающего электрона.h – постоянная Планка.A – работа выхода электрона из металла.(m(vmax)^2)/2 – максимальная кинетическая энергия фотоэлектрона.Уравнение Эйнштейна позволяет объяснить II и III законы фотоэффекта. Из уравнения выше непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни v от интенсивности света не зависят (2 закон фотоэффекта). Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (для данного металла А – константа), то при некоторой достаточно малой частоте v=v0 кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится (3 закон фотоэффекта).Зависимость фототока от разности потенциалов между анодом А и катодом К называется вольтамперной характеристикой (ВАХ) вакуумного фотодиода. 7. Соотношение неопределенностей Гейзенберга. Соотношение неопределенностей задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Для микрочастиц неприемлемо понятие траектории, т.е. невозможно одновременно точно определить все динамические переменные, описывающие состояние частицы, у частицы не могут быть одновременно точно измерены положение и импульс где
Произведение
неопределенностей двух сопряженных
элементов не может быть по порядку
величины меньше постоянной Планка
|
Вопрос 3:Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой.Закон Кирхгофа: Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы. Для абсолютно чёрного тела функция зависящая от температуры и частоты совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности.Закон Стефана — Больцмана:Мощность излучения абсолютно чёрного тела (интегральная мощность по всему спектру), приходящаяся на единицу площади поверхности, прямо пропорциональна четвёртой степени температуры тела:Р = SϵσТ4 Закон Вина:длина волны, на которой абсолютно черное тело излучает наибольшее количество энергии, обратно пропорциональна температуре этого тела λмах=К/Т где К - коэффициент пропорциональности или постоянная закона Вина. К=0,289 см. Абсолютно черным телом называется поверхность, полностью поглощающая излучение, падающее на неё. Понятие абсолютно черного тела исключительно теоретическое: в действительности объектов с такой идеальной поверхностью, полностью поглощающей все волны, не существует. 4. Распределение энергии в спектре абсолютно черного тела. Формула Рэлея-Джинса. Ультрафиолетовая катастрофа. Закон Рэлея-Джинса Попытка описать излучение абсолютно чёрного тела исходя из классических принципов термодинамики и электродинамики приводит к закону Рэлея — Джинса:
Эта
формула предполагает квадратичное
возрастание спектральной
плотности излучения в зависимости
от его частоты. На практике такой
закон означал бы невозможность
термодинамического
равновесия между веществом и излучением,
поскольку согласно ему вся тепловая
энергия должна была бы перейти в
энергию излучения коротковолновой
области спектра. Такое гипотетическое
явление было названо ультрафиолетовой
катастрофой. Тем не менее закон
излучения Рэлея — Джинса справедлив
для длинноволновой области спектра
и адекватно описывает характер
излучения. Объяснить факт такого
соответствия можно лишь при использовании
квантово-механического подхода,
согласно которому излучение происходит
дискретно. Исходя из квантовых законов
можно получить формулу
Планка, которая будет совпадать с
формулой Рэлея — Джинса при Правильно описывал низкочастотную часть спектра, при средних частотах приводил к резкому расхождению с экспериментом, а при высоких — к абсурдному результату означавшему неудовлетворительность классической физики. Формулы Рэлея-Джинса:
.
Ультрафиоле́товая катастро́фа — физический термин, описывающий парадокс классической физики, состоящий в том, что полная мощность теплового излучения любого нагретого тела должна быть бесконечной. Название парадокс получил из-за того, что спектральная плотность энергии излучения должна была неограниченно расти по мере сокращения длины волны. По сути этот парадокс показал если не внутреннюю противоречивость классической физики, то во всяком случае крайне резкое (абсурдное) расхождение с элементарными наблюдениями и экспериментом. Так как это не согласуется с экспериментальным наблюдением, в конце XIX века возникали трудности в описании фотометрических характеристик тел. Проблема была решена при помощи квантовой теории излучения Макса Планка в 1900 году.
|
5.Квантовая
гипотеза и формула Планкаю. Фотоны.
Гипо́теза
Пла́нка — гипотеза,
выдвинутая 14
декабря 1900
года Максом
Планком и
заключающаяся в том, что при тепловом
излучении энергия
испускается и поглощается не непрерывно,
а отдельными квантами(порциями).
Каждая такая порция-квант имеет
энергию
Формула
Планка была получена после того, как
стало ясно, что формула Рэлея
— Джинса
удовлетворительно описывает излучение
только в области длинных волн. Для
вывода формулы Планк в 1900 году сделал
предположение о том, что электромагнитное
излучение испускается в виде отдельных
порций энергии (квантов), величина
которых связана с частотой излучения
выражением:
. |
|
6. ЭФФЕКТ КОМПТОНА И ЕГО ТЕОРИЯ Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучения вследствие упругого рассеивания его электронами. Обнаружен американским физиком Артуром Комптоном в 1923 году для рентгеновского излучения. В 1927 Комптон получил за это открытие Нобелевскую премию по физике.
Иллюстрация к эффекту Комптона
При
рассеянии фотона на
покоящемся электроне частоты
фотона
где Перейдя к длинам волн:
где
Для электрона Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волна является непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны, другими словами подтверждает существование фотонов. Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.
Обратный комптон-эффект. Если электроны, на которых рассеивается электромагнитное излучение, являются релятивистскими (то есть движутся со скоростями, близкими к скорости света), то при упругом рассеянии длина волны излучения будет уменьшаться, то есть энергия (и импульс) фотонов будет увеличиваться за счет энергии (и импульса) электронов. Это явление называют обратным К. э. Обратный К. э. часто привлекают для объяснения механизма излучения космических рентгеновских источников, образования рентгеновской компоненты фонового галактического излучения, трансформации плазменных волн в электромагнитные волны высокой частоты.
9. Модель атома. Постулаты Бора. а) Модель атомов Томпсона – атом представляет собой шар, который равномерно заполнен положительным зарядом, внутри которого расположены электроны, колеблющиеся около положения равновесия, общий заряд равен заряду электронов б) Модель Резерфорда – В опыте Резерфорда альфа-частицы рассеивались под всевозможными углами, вплоть до обратного. Атом состоит из очень маленького образования – ядра, в котором сосредоточена практически вся масса атома и весь положительный заряд. Вокруг ядра по орбитам движутся электроны. Недостаток теории Резерфорда – т.к. электроны излучают свет, они теряют энергию, в результате радиус орбиты движения должен постоянно уменьшаться. в) Модель Бора - атом может находиться только в особенных стационарных, или квантовых, состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн. - электроны могут двигаться не по бесконечному множеству орбит, а только по некоторым дискретным орбитам, названным стационарными. Двигаясь по стационарным орбитам, электроны не излучают. - при переходе с одной стационарной орбиты на другую электрон излучает или поглощает квант энергии 12. Частица в потенциальной яме. Потенциа́льная
я́ма – область пространства, где
присутствует локальный минимум
потенциальной энергии частицы. Если
в потенциальную яму попала частица,
энергия которой ниже, чем необходимая
для преодоления краёв ямы, то возникнут
колебания частицы в яме. Амплитуда
колебаний будет обусловлена собственной
энергией частицы. Частица, находящаяся
на дне потенциальной ямы, пребывает
в состоянии устойчивого равновесия,
то есть при отклонении частицы от
точки минимума потенциальной энергии
возникает сила, направленная в
противоположную отклонению сторону.
Если частица подчиняется квантовым
законам, то даже несмотря на недостаток
энергии она с определённой вероятностью
может покинуть потенциальную яму
(явление туннельного эффекта). В
квантовой физике частица, движущаяся
в свободном пространстве, может
обладать любой энергией. Ее энергетический
спектр – сплошной. У частицы, которая
движется в силовом поле, удерживающем
ее в ограниченной области пространства,
спектр собственных значений энергии
оказывается дискретным. Примером
может служить финитное (т. е. ограниченное)
движение электрона в кулоновском поле
ядра атома водорода. Дискретность
энергетических уровней частиц, запертых
в ограниченной области, вытекает из
двойственной природы частиц и является
принципиальным отличием квантовой
физики от классической. Простой
физической моделью финитного движения
может служить движение частицы в
одномерной «потенциальной яме» с
бесконечно высокими стенками. Частица
не может покинуть область размером
L. Она движется в этой области, испытывая
многократные отражения от стенок. С
волновой точки зрения между стенками
во встречных направлениях движутся
две волны де Бройля. Это напоминает
картину двух встречных волн, бегущих
по струне с закрепленными концами.
Как и в случае струны, стационарным
состояниям соответствуют стоячие
волны, которые образуются при условии,
что на длине L укладывается целое число
полуволн: L = n · (λ / 2) (n = 1, 2, 3, ...)
Таким
образом, стационарным состояниям
частицы, запертой в потенциальной
яме, соответствует дискретный набор
длин волн. Поскольку в квантово-механическом
случае длина волны λ однозначно связана
с импульсом частицы: λ = h / p, а импульс
частицы определяет энергию ее движения:
E = p2 / (2m) (нерелятивистское приближение),
то квантованной оказывается и энергия
частицы. Квантово-механический расчет
приводит к следующему выражению:
Действительно,
у покоящейся частицы импульс строго
равен нулю, следовательно, Δpx = 0. В то
же время неопределенность координаты
частицы Δx ≈ L. Поэтому произведение
Δx · Δpx у частицы, лежащей на дне
потенциальной ямы, должно было бы
равняться нулю. Соотношение
неопределенностей позволяет сделать
оценку минимальной энергии E1 частицы.
Если принять, что в состоянии с
минимальной энергией px ≈ Δpx, то для
минимальной энергии E1 получается
выражения
Эта грубая оценка дает правильное по порядку величины значение E1. Стоячие волны де Бройля, образующиеся при движении частицы в потенциальной яме, это и есть волновые или пси-функции, с помощью которых квантовая механика описывает стационарные состояния микрообъектов. Квадрат модуля |Ψ|2 волновой функции определяется как вероятность нахождения частицы в различных точках пространства. В компьютерной модели можно изменять ширину L потенциальной ямы, а также массу m запертой в ней частицы. В левом окне высвечиваются графические изображения волновых функций Ψ(x) или квадратов их модулей |Ψ|2 для нескольких стационарных состояний (n = 1–5). В правом окне изображается энергетический спектр частицы, то есть спектр возможных значений ее энергии. Обратите внимание, что энергетические уровни опускаются при увеличении ширины L потенциальной ямы и массы m запертой в ней частицы.
10. Гипотеза де Бройля. Экспериментальное подтверждение волновых свойств микрочастиц. Гипотеза
де Бройля заключается в том, что
французский физик Луи де Бройль
выдвинул идею приписать волновые
свойства электрону. Проводя аналогию
между квантом, де Бройль предположил,
что движение электрона или какой-либо
другой частицы, обладающей массой
покоя, связано с волновым процессом.
Гипотеза де Бройля устанавливает,
что движущейся частице, обладающей
энергией E и импульсом p, соответствует
волновой процесс, частота которого
равна: Впервые
гипотеза де Бройля была подтверждена
экспериментально в опытах по дифракции
электронов американскими физиками
К. Дэвиссоном (C.Devisson) и Л. Джермером
(L. Germer). Схема опыта представлена на
рис.2. Параллельный моноэнергетический
пучок электронов, получаемый с помощью
электронно-лучевой трубки 1, направляется
на мишень 2 (монокристалл никеля).
Отраженные электроны улавливаются
коллектором 3, соединенным с
гальванометром. Коллектор можно
устанавливать под любым углом
относительно падающего луча.
Рассмотрим результаты опытов
Дэвиссона и Джермера. Например, в одном
из опытов наблюдалась дифракция
электронов с энергией 54 эВ. Первый
дифракционный максимум наблюдался
под углом j = 50о (см. рис.2). Импульс
электрона связан с его кинетической
энергией формулой
В
то же время по формуле Брегга для
максимума первого порядка при дифракции
на кристалле никеля с периодом решетки
d = 0,091 нм получаем:
17(Лекция
2006 года)
Контактные
явления в электрических аппаратах
Контактная система
является одной из наиболее существенных
частей электроаппарата, от надежной
работы которой существенно зависит
работоспособность всего
аппарата.Электрический
контакт –
это сопротивление
тел,
обеспечивающее протекание тока в
электрической цепи.
Конструктивный
узел, с помощью которого в процессе
работы аппарата производятся
периодические замыкания и размыкания
электрической цепи, называется
электрическим
контактным соединение.
Контактное
соединение состоит в большинстве
случаев из
подвижного и неподвижного элементов.
Поверхность
соприкосновения проводников носит
название контактной поверхности.тНаличие
шероховатости и волнистости поверхности
соприкосновения контактов приводит
к тому, что соприкосновение контактов
всегда совершается в отдельных точках.
Их количество зависит от нагрузки
(силы сжатия
контактов),
температуры,
механических свойств
контактного материала и его
геометрических очертаний.
Благодаря
нажатию контактов вершины выступов
деформируются и образуются площади
действительного касания контактов.
В результате
стягивания линий тока к площадкам
касания их длина увеличивается, а
сечение проводника, через которое
фактически проходит ток, уменьшается,
что вызывает увеличение сопротивления.Такое
сопротивление называется переходным
сопротивлением стягивания контакта
Rст.
Оно пропорционально удельному
сопротивлению материала контакта ,
корню квадратному от временного
сопротивления на смятие этого материала
и обратно пропорционально корню
квадратному из силы контактного
нажатия Рконт
Как
видно из приведенного графика с
ростом контактного нажатия Рконт
переходное сопротивление уменьшается.
При многократных замыканиях и
размыканиях контактов кривые не
повторяют друг друга, так как в каждом
случае касание происходит в различных
точках. Таким образом, полное
сопротивление контактного соединения
состоит из двух составляющих:
сопротивление собственного материала
контактных элементов и переходного
сопротивления в месте их соприкосновения,
т.е.
Размеры контактной поверхности мало влияет на контактное сопротивление, так как одновременно с увеличением числа точек действительного соприкосновения уменьшаются нажатие на единицу поверхности и ее смятия. Размеры поверхности контакта имеет значение для условий нагрева, так как с их увеличением увеличивается теплоемкость и поверхность охлаждения. При том же сопротивлении большие по размеру контакты допускают большую нагрузку по току. Обработка поверхности контакта также влияет на его переходное сопротивление контакта уменьшается. Переходное сопротивление шлифованных контактов выше, чем контактов с более грубой обработкой. - влияние силы нажатия. В области малых усилий на контакт наблюдается резкое увеличение переходного сопротивления. При очень больших силах нажатия величина переходного сопротивления контактов меняется чрезвычайно незначительно. Кроме того, слишком большие силы нажатия вызывают чрезмерные напряжения в материале контактов, вследствие чего утрачивается их упругость, они становятся менее прочными. Каждый металл характеризуется определенным оптимальным значением усилия, обеспечивающим предельное давление, выше которого переходное сопротивление практически остается неизменным.
|
13вопрос:
Мы
нашли одно частное решение для свободной
частицы, когда не было потенциальной
энергии, рассмотрим сейчас задачу
чуть более сложную. Пусть потенциальная
энергия имеет вид
Решение уравнения (8.1) пишем немедленно (это уравнение колебаний):
Уравнение
в области
Мы
рассматриваем первый
случай,
когда энергия частицы больше, чем
напряжение в цепи:
Эти решения надо состыковать. Функция должна быть это непрерывной:
У
нас четыре константы, а мы имеем два
уравнения. Математик, конечно, озадачился
бы, но мы должны интерпретировать
результат. Прежде всего смотрим на
функцию u1:
Мы
видим, что
Вот электроны, летящие с кинетической энергией, входят в область электрического поля, которое оказывает тормозящую силу, но их энергия больше, чем работа по преодолению этого поля. По классическим понятиям все электроны проходят этот конденсатор и дальше идут с меньшей энергией, здесь мы получаем, что существует отличная от нуля вероятность (тем больше, чем больше C2), что электрон отразится от этого поля и полетит обратно, при чём с той же энергией, с которой он летел. Чтобы драматизировать пример: ставим абсолютно твёрдое, но непробиваемое стекло, и вы стреляете в него из пулемёта. Нормальные пули стекло пробивают, но по правилам игры, которые мы тут обнаруживаем, есть отличная от нуля вероятность, что пуля отразится всё-таки от стекла и попадёт стрелку в лоб. Мы
рассматривали прохождение частицы
через потенциальный барьер. Мы нашли
решение для этой ситуации в случае,
когда x<0
и когда
15 вопрос: Полупроводники – вещества, у которых ширина запрещённой зоны составляет величину порядка 1 эВ. Примесная проводимость. Рассмотрим полупроводник, в котором часть атомов основного полупроводника заменена атомами вещества валентность, которых отличается валентностью основного полупроводника. Пусть в 4х валентных полупроводниках внедрены атомы 5валентной примеси. В случае 5валентной примеси 4 электрона этой примеси будут задействованы в образовании межатомных связей в кристалле. 5й элемент примеси в создании связи не участвуют, и поэтому оказывается слабосвязываемым в атомной примеси. При увеличении температуры полупроводника отрывается прежде всего этот 5й электрон, при этом образуются свободные электроны, но дырки при этом не образуются. Такая примесь называется донорной примесью. В случае донорной примеси проводимость полупроводника является электронной, а сам полупроводник называется полупроводник n-типа. Рассмотрим 4х валентный полупроводник в который внедрена 3х валентная примесь. В этом случае одна из связей оказывается недоукомплектованной электроном. Эту связь может доукомплектовать электрон из соседней связи основного полупроводника. При этом свободные электроны не появляются. Такая примесь называется акцепторной. А сам полупроводник – полупроводником p-типа. Собственная проводимость. Химические чистые вещества являются собственными полупроводниками. Рассмотрим 4хвалентный полупроводник Ge (германий). Четыре связи с соседними атомами, образованы восемью эл-нами (по четыре от каждого атома). Каждый электрон обретает связь с противоположно направленными спинами. При низкой температуре все связи оказываются укомплектованными электронами и свободных электронов в полупроводнике нет. При увеличении температуры за счет энергии химического движения происходит отрыв электронов от одной из связи. При этом на месте ушедшего электрона остается дырка. Дырка локализована на какой-то одной связи в кристалле и свободно перемещаться по кристаллу не может. Оторвавшийся же электрон может свободно перемещаться по кристаллу. Если приложить внешнее электрическое поле, то электрон будет перемещаться против поля. Дырку же может занять электрон из соседней связи. Путем таких перескоков дырка будет перемещаться по полю, а электрон против поля. Движение дырки можно рассмотреть как движение положительно заряженных частиц. Когда свободный электрон занимает место дырки исчезает одновременно и свободный электрон и дырка. Такой процесс называется рекомбинацией. Т. е. в химически чистых полупроводниках появляются одновременно свободные электроны и дырка, причем количество их одинаково. Проводимость собственных полупроводников являются электронно-дырочными. 14 Вопрос Прежде всего, я хотел бы остановиться на тех основных предпосылках, на которых базируется зонная теория твёрдого тела. Что представляет собой кристалл с физической точки зрения? Это есть дом, в котором живёт целое семейство электронов. Этот дом имеет определённую архитектуру, и населяющие его электроны подчиняются определённым правилам внутреннего распорядка. Задача заключается в описании поведения этих электронов. Электроны, наполняющие кристалл, находятся во взаимодействии друг с другом. Учёт этого взаимодействия представляет собой основную и принципиальную трудность теории. Это является трудностью потому, что квантовая механика не умеет точно решать задачу о системе взаимодействующих частиц. При решении таких задач квантовая механика довольствуется приближёнными методами.Поэтому теория кристалла по самому существу своему является приближённой теорией. Остаётся заботиться лишь о том, чтобы эта теория представляла собой достаточно хорошее приближение. Задача о кристалле была бы совсем простой задачей, если бы можно было пренебречь взаимодействием между электронами, сохранив только взаимодействие электронов с ядрами. Этот неправильный, конечно, путь может быть несколько исправлен, если взаимодействие электронов заменить введением некоторого внешнего эффективного силового поля, в котором каждый электрон движется независимо от остальных. Такое эффективное поле, вычисляемое как поле, созданное размазанным зарядом всех электронов нашей системы, называется самосогласованным полем. Учёт взаимодействия методом самосогласованного поля — это весьма несовершенный способ учёта взаимодействия. Этот метод, однако, привлекателен тем, что он позволяет многоэлектронную задачу превратить в серию независимых между собой одноэлектронных задач. Пользуясь этим методом, мы имеем право говорить о поведении каждого электрона в отдельности, приписывать каждому электрону свою индивидуальную волновую функцию и своё индивидуальное значение энергии. В рамках этого метода каждый электрон живёт своей индивидуальной жизнью, как бы ≪не замечая≫ остальных электронов, так, как если бы других электронов вовсе не существовало. Единственное, что напоминает ему о них, это — принцип Паули, запрещающий ему занимать квантовые состояния, уже занятые другими электронами. Именно на этом методе, методе самосогласованного поля, и основана так называемая зонная теория твёрдого тела. Итак, в основе зонной теории лежит сведение многоэлектронной задачи к задаче одноэлектронной. Зонная теория — это теория одного электрона. Это является первой, но не единственной характерной чертой зонной теории. Второй характерной чертой является определённое предположение о характере того силового поля, в котором движется каждый отдельный электрон. Это поле имеет периодический характер, отражая в себе периодическую структуру решётки. Для зонной теории не существенно, каков конкретный вид этого поля. Существенно лишь, что это поле периодично с периодом решётки. Характерная зонная структура энергетического спектра электрона, т. е. система разрешённых полос энергии, разделённых, вообще говоря, запрещёнными участками, есть результат именно этой периодичности. Таким образом, зонная картина спектра содержится уже в самых предпосылках теории: в предположении о периодическом характере потенциала. Отметим некоторые характерные недостатки зонной теории, некоторые её особенности, скрытые уже в самой постановке задачи. Если считать электроны ≪не замечающими≫ друг друга, то не исключается возможность скопления их на одном и том же атоме. Может случиться, что на одном и том же атоме (или ионе) сосредоточится сразу несколько электронов за счёт оголения какого-нибудь другого или каких-нибудь других атомов (или ионов). Такие состояния, характеризующиеся ≪переконцентрацией≫ электронов в одном месте, фигурируют в зонной теории наравне с прочими. Когда атом решётки получает на себя лишний электрон (сверх нормального комплекта), то такой атом превращается в отрицательный ион. Этот лишний электрон заимствуется от другого атома, который при этом превращается в положительный ион. Здесь существен не столько сам тот факт, что зонная теория допускает пересаживание электрона с одного атома решётки на любой другой атом, сколько то, что такое пересаживание, с точки зрения зонной теории, не требует затраты энергии. Зонная теория представляет собой приближённую теорию и, следовательно, имеет свои пределы применимости. Существуют задачи, для которых приближения, лежащие в основе зонной теории, приемлемы. С другой стороны, существуют такие задачи, для которых такие приближения неприемлемы. Сформулируем условия, определяющие сферу применимости зонной теории. Можно указать четыре таких условия. 1) Каждый атом (или ион), входящий в состав кристаллической решётки, обладает своим нормальным комплектом электронов. К этим ≪собственным≫ электронам, принадлежащим атомам или ионам решётки, зонная теория заведомо неприменима. Поведение этих электронов не может быть правильно описано в рамках зонной теории. 2) Зонная теория даёт правильное описание поведения этих ≪лишних≫ электронов опять-таки не всегда, а лишь до тех пор, пока концентрация этих ≪лишних≫ электронов достаточно мала. Иначе говоря, для зонной теории необходимо, чтобы число аномальных атомов (ионов) было мало бы по сравнению с общим числом атомов (ионов) в решётке. 3) Предыдущее условие является необходимым, но не достаточным. Зонная теория применима к ≪лишним≫ электронам лишь при условии, что ≪лишний≫ электрон не меняет состояния '≪собственных≫ (внутренних) электронов того атома (или иона), на который этот ≪лишний≫ электрон посажен. Это имеет место, например, в том случае, когда ≪собственные≫ электроны атома (или иона) образуют замкнутую оболочку. 4) При соблюдении всех предыдущих условий зонная теория всё же перестаёт действовать в тех задачах, в которых существенно взаимодействие между двумя или несколькими ≪лишними≫ электронами. Иначе говоря, зонная теория неприменима к тем задачам, в которых мы имеем дело со встречей двух аномальных атомов (или ионов), когда эти два аномальных атома (или иона) оказываются по соседству друг с другом и вступают во взаимодействие между собой. Сформулированные выше условия относятся вообще к зонной теории, как к методу описания поведения электронов в решётке, независимо от того, идёт ли речь о металлической или неметаллической решётке. В заключение спросим себя: каково же в итоге положение дел в современной теории твёрдого тела и каковы перспективы её дальнейшего развития? Мы имеем в настоящее время достаточно развитую электронную теорию металлов. Эта теория достаточно развита с точки зрения своих применений, хотя её нельзя признать достаточно развитой с точки зрения своего обоснования. Задача теории металлов заключается, быть может, не только в том (или, лучше сказать, не столько в том), чтобы построить хорошую и строгую теорию, сколько в том, чтобы понять, почему заведомо плохая теория (теория Блоха или даже теория Зоммерфельда) даёт достаточно хорошие результаты. Что же касается теории неметаллических кристаллов, то здесь мы имеем достаточно развитую так называемую зонную теорию и, кроме того, ряд отдельных теоретических работ, лежащих вне рамок зонной теории. Зонная теория служит до сих пор в руках экспериментаторов той рабочей схемой, с помощью которой интерпретируются разнообразные процессы, протекающие в неметаллических кристаллах. В эту схему часто вкладывается узко блоховское, совершенно неправильное содержание, которого на самом деле эта схема не имеет. Однако даже при правильном её толковании зонную схему нельзя признать ни достаточно совершенной, ни достаточно всеобъемлющей. Тем не менее, в теории неметаллических кристаллов существует определённый и довольно обширный круг задач, которые могут решаться в рамках зонной схемы. Мы имеем здесь очень богатый экспериментальный материал, который ещё далеко не весь уложен в теорию. Дальнейшее развитие зонной теории (на которое она имеет полное право при правильном её понимании), развитие её под углом зрения расширения того экспериментального материала, который ею охватывается и интерпретируется, — это одно из направлений в дальнейшем развитии теории неметаллических кристаллов. Другое направление, которое нам кажется более интересным, более принципиальным и более многообещающим, — это развитие теории твёрдого тела вне рамок зонной теории. На этом пути сделано ещё очень мало. Существует целый ряд задач, которые могут получить удовлетворительное решение только на этом втором, а не на первом пути. Первый путь, в котором задача об электронах в кристалле рассматривается как задача об одном электроне (или об одной дырке), движущемся в периодическом поле, может дать объяснение многим ещё не объяснённым экспериментальным фактам, но на этом пути вряд ли можно ожидать сейчас чего-нибудь принципиально нового. Второй путь, в котором задача об электронах в кристалле решается как многоэлектронная задача (без сведения её к одноэлектронной задаче и к периодическому полю), может не только дать объяснение тем или иным фактам, но на этом пути могут быть раскрыты совершенно новые и, быть может, неожиданные особенности в поведении электронов. 18(Другой ресурс): Понятие о квантовой статистике Бозе — Эйнштейна и Ферми — Дирака Одним из важнейших «объектов» изучения квантовой статистики, как и классической, является идеальный газ. Это связано с тем, что во многих случаях реальную систему можно в хорошем приближении считать идеальным газом. Состояние системы невзаимодействующих частиц задается с помощью так называемых чисел заполнения Ni — чисел, указывающих степень заполнения квантового состояния (характеризуется данным набором i квантовых чисел) частицами системы, состоящей из многих тождественных частиц. Для систем частиц, образованных бозонами — частицами с нулевым или целым спином (см. § 226), числа заполнения могут принимать любые целые значения: 0, 1, 2, ... (см. § 227). Для систем частиц, образованных фермионами — частицами с полуцелым спином (см. § 226), числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых (см. § 227). Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения Ni. Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна.* Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым (см. § 227):
* Ш. Бозе (1894—1974) — индийский физик. Это распределение называется распределением Бозе — Эйнштейна. Здесь Ni — среднее число бозонов в квантовом состоянии с энергией Ei, k — постоянная Больцмана, Т—термодинамическая температура, —химический потенциал; не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех Ni равна полному числу частиц в системе. Здесь 0, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы. Динамика и законы сохранения в механике Идеальный
газ из фермионов — ферми-газ —
описывается квантовой статистикой
Ферми — Дирака.* Распределение фермионов
по энергиям имеет вид
|
8. Нестационарное
и стационарное уравнение Шредингера.
Т.к.
поведение микрочастицы не может быть
однозначно описано характеристиками
механики, необходимо было ввести
функцию, описывающую это состояние
на основе подходов квантовой механики
– волновая функция. ВФ – комплексная
функция координат и времени, которая
находится в результате уравнения
Шредингера.
Пусть волновая
функция задана в n-мерном конфигурационном
пространстве, тогда в каждой точке с
координатами
где
Стационарное уравнение Шрёдингера - уравнение Шрёдингера, не содержащее времени.
Частное
решение для специального случая,
когда
где
функция
которое
получается из уравнения Шрёдингера (1) при
подстановке в него указанной выше
формулы для
11. Волновая функция, ее свойства и статистический смысл. Необходимость
вероятностного подхода к описанию
микрочастиц является важнейшей
отличительной особенностью квантовой
теории. Можно ли волны де Бройля
истолковывать как волны вероятности,
т.е. считать, что вероятность обнаружить
микрочастицу в различных точках
пространства меняется по волновому
закону? Такое толкование волн де Бройля
уже неверно, хотя бы потому, что тогда
вероятность обнаружить частицу в
некоторых точках пространства может
быть отрицательна, что не имеет смысла.
Чтобы устранить эти трудности, немецкий
физик М. Борн в 1926 г. предположил, что
по волновому закону меняется не сама
вероятность, а величина, названная
амплитудой вероятности и обозначаемая
Вероятность
найти частицу в момент времени t в
конечном объеме V, согласно теореме
сложения вероятностей, равна
Волновая функция
удовлетворяет принципу суперпозиции:
если система может находиться в
различных состояниях, описываемых
волновыми функциями
16(Лекция
с интернета) Радиоактивностью называется
способность атомных ядер к
самопроизвольному превращению в
другие ядра с испусканием одной или
нескольких заряженных частиц и фотонов.
Ядра, обладающие свойством самопроизвольно
распадаться, называются радиоактивными, а
ядра, не имеющие таких свойств
– стабильными. Из
более чем 1700 известных в настоящее
время нуклидов, только 200 стабильны.
Большинство радионуклидов получено
искусственно.
Все
встречающиеся в природе элементы с
атомными номерами > 83 (висмут) –
радиоактивны. Они представляют собой
отдельные звенья последовательных
превращений – радиоактивные
ряды.
Существует четыре ряда радиоактивных
превращений: три естественных (ряды
урана-235, урана-238 (актиноурана, AcU),
тория-232) и один искусственный (ряд
нептуния). Характерной особенностью
трех естественных семейств является
наличие в ряду превращений газообразных
радиоактивных продуктов – изотопов
радона. Как видно из схем превращений,
в некоторых случаях возможны два пути
перехода одного и того же изотопа в
два новых элемента с одной и той же
скоростью в результате альфа- и
бета-распада. Это так называемые
«вилки» – одни и те же ядра с разными
вероятностями претерпевают различные
типы радиоактивного распада. Более
вероятен тот процесс, по которому
осуществляется превращение большей
доли ядер. Обычно на схемах радиоактивных
семейств в случае «вилок» под типом
распада в скобках обозначена доля (%)
превращающихся ядер.
Атомное
ядро содержит более 99, 95% всей массы
атома, имеет размеры порядка 10-12 –
10-13 см.
Атомные ядра состоят из элементарных
частиц – протонови нейтронов,
их массы близки между собой. Протон
электрически положителен (его заряд
равен заряду электрона), нейтрон –
электрически нейтрален. Протон и
нейтрон, входящие в состав атомного
ядра, объединяются под общим
названием нуклон. Общее
число нуклонов в ядре называется массовым
числом и
обозначается через А. Число протонов
в ядре называется атомным
номером химического
элемента (Z, зарядное число). Число
нейтронов в ядре обозначается через
N. В нормальном состоянии атом
электрически нейтрален. Химические
свойства атома определяются особенностями
структуры его электронных оболочек
и числом электронов. Тип атомного ядра
обозначают:
|


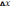 – величина среднеквадратичного
отклонения координаты,
– величина среднеквадратичного
отклонения координаты, 
 - среднеквадратического отклонения
импульса, h
– приведенная постоянная Планка.
- среднеквадратического отклонения
импульса, h
– приведенная постоянная Планка.


 .Закон
Рэлея-Джинса —
закон
излучения Рэлея-Джинса для равновесной
плотности излучения абсолютно
чёрного тела
.Закон
Рэлея-Джинса —
закон
излучения Рэлея-Джинса для равновесной
плотности излучения абсолютно
чёрного тела  и
для испускательной
способности абсолютно
чёрного тела
и
для испускательной
способности абсолютно
чёрного тела 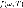 который
получили Рэлей и Джинс,
в рамках классической статистики
(теорема о равнораспределении энергии
по степеням свободы и представление
об электромагнитном поле как о
бесконечномерной динамической
системе).
который
получили Рэлей и Джинс,
в рамках классической статистики
(теорема о равнораспределении энергии
по степеням свободы и представление
об электромагнитном поле как о
бесконечномерной динамической
системе).
 .
.
 ,
пропорциональной частоте ν излучения:
,
пропорциональной частоте ν излучения: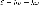 тбьгде h или
тбьгде h или 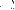 —
коэффициент пропорциональности,
названный впоследствии постоянной
Планка.
На основе этой гипотезы он предложил
теоретический вывод соотношения
между температурой тела
и испускаемым этим телом
излучением — формулу
Планка.
Позднее
гипотеза Планка была
подтверждена экспериментально.
Выдвижение
этой гипотезы считается моментом
рождения квантовой
механики.
Формула
Планка —
выражение для спектральной плотности
мощности излучения абсолютно чёрного
тела, которое было получено Максом
Планком.
Для плотности энергии излучения u(ω,T):
—
коэффициент пропорциональности,
названный впоследствии постоянной
Планка.
На основе этой гипотезы он предложил
теоретический вывод соотношения
между температурой тела
и испускаемым этим телом
излучением — формулу
Планка.
Позднее
гипотеза Планка была
подтверждена экспериментально.
Выдвижение
этой гипотезы считается моментом
рождения квантовой
механики.
Формула
Планка —
выражение для спектральной плотности
мощности излучения абсолютно чёрного
тела, которое было получено Максом
Планком.
Для плотности энергии излучения u(ω,T):
 Коэффициент пропорциональности
Коэффициент пропорциональности  впоследствии
назвали постоянной
Планка,
впоследствии
назвали постоянной
Планка,  =
1.054 · 10−27 эрг·с
Фото́н (от др.-греч.
«свет») — элементарная
частица, квант электромагнитного
излучения (в
узком смысле —света).
Это безмассовая
частица, способная существовать
только двигаясь со скоростью
света. Электрический
заряд фотона
также равен
нулю. Фотон может находиться только
в двух спиновых состояниях с
проекцией спина на
направление движения (спиральностью)
±1. Этому свойству в классической
электродинамике соответствует
круговая правая и левая поляризация
электромагнитной волны. Фотону как
квантовой частице
свойственен корпускулярно-волновой
дуализм, он проявляет одновременно
свойства частицы и волны.
Фотоны обозначаются буквой
=
1.054 · 10−27 эрг·с
Фото́н (от др.-греч.
«свет») — элементарная
частица, квант электромагнитного
излучения (в
узком смысле —света).
Это безмассовая
частица, способная существовать
только двигаясь со скоростью
света. Электрический
заряд фотона
также равен
нулю. Фотон может находиться только
в двух спиновых состояниях с
проекцией спина на
направление движения (спиральностью)
±1. Этому свойству в классической
электродинамике соответствует
круговая правая и левая поляризация
электромагнитной волны. Фотону как
квантовой частице
свойственен корпускулярно-волновой
дуализм, он проявляет одновременно
свойства частицы и волны.
Фотоны обозначаются буквой  ,
поэтому их часто называют гамма-квантами (особенно
фотоны высоких энергий);
эти термины практически синонимичны.
С точки зрения Стандартной
модели фотон
является калибровочным
бозоном. Виртуальные фотоны
являются
переносчиками электромагнитного
взаимодействия, таким образом
обеспечивая взаимодействие, например,
между двумя электрическими
зарядами. Фотон —
самая распространённая по численности
частица во Вселенной.
,
поэтому их часто называют гамма-квантами (особенно
фотоны высоких энергий);
эти термины практически синонимичны.
С точки зрения Стандартной
модели фотон
является калибровочным
бозоном. Виртуальные фотоны
являются
переносчиками электромагнитного
взаимодействия, таким образом
обеспечивая взаимодействие, например,
между двумя электрическими
зарядами. Фотон —
самая распространённая по численности
частица во Вселенной.
 и
и  (до
и после рассеяния соответственно)
связаны соотношением:
(до
и после рассеяния соответственно)
связаны соотношением:
 —
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
—
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
 — комптоновская
длина волны электрона.
— комптоновская
длина волны электрона. м.
Уменьшение энергии фотона после
комптоновского
рассеяния называется комптоновским
сдвигом.
В классической электродинамике
рассеяние электромагнитной волны на
заряде (томсоновское
рассеяние) не сопровождается
уменьшением её частоты.
м.
Уменьшение энергии фотона после
комптоновского
рассеяния называется комптоновским
сдвигом.
В классической электродинамике
рассеяние электромагнитной волны на
заряде (томсоновское
рассеяние) не сопровождается
уменьшением её частоты. Здесь m – масса частицы, h –
постоянная Планка, E1 = h2 / (8mL2) – энергия
наинизшего состояния. Следует обратить
внимание, что квантово-механическая
частица в отличие от классической не
может покоиться на дне потенциальной
ямы, то есть иметь энергию E1 = 0. Это
противоречило бы соотношению
неопределенностей Δx · Δpx ≥ h.
Здесь m – масса частицы, h –
постоянная Планка, E1 = h2 / (8mL2) – энергия
наинизшего состояния. Следует обратить
внимание, что квантово-механическая
частица в отличие от классической не
может покоиться на дне потенциальной
ямы, то есть иметь энергию E1 = 0. Это
противоречило бы соотношению
неопределенностей Δx · Δpx ≥ h.

 а длина волны:
а длина волны:
 где
p - импульс движущейся частицы.
где
p - импульс движущейся частицы. .
Из формулы де Бройля определяем длину
волны электронов:
.
Из формулы де Бройля определяем длину
волны электронов:


 Оба результата
хорошо совпадают, что подтверждает
наличие волновых свойств у электронов.
Экспериментальная проверка волновой
природы частиц продолжалась и в
последующие годы. В 1928 - 30 гг. О. Штерн
(O. Stern) и И. Эстерман (I. Estermann) провели
опыты по дифракции атомов гелия, неона,
молекул водорода и дейтерия на
кристаллах.
Оба результата
хорошо совпадают, что подтверждает
наличие волновых свойств у электронов.
Экспериментальная проверка волновой
природы частиц продолжалась и в
последующие годы. В 1928 - 30 гг. О. Штерн
(O. Stern) и И. Эстерман (I. Estermann) провели
опыты по дифракции атомов гелия, неона,
молекул водорода и дейтерия на
кристаллах.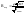

 .
На величину переходного сопротивления
оказывает влияние ряд факторов:
- влияние
материала контакта.
Величина напряжения смятия
при смятии материала от прижатия
поверхностей контактов S
внешней силой F
зависит от твердости используемого
материала
.
На величину переходного сопротивления
оказывает влияние ряд факторов:
- влияние
материала контакта.
Величина напряжения смятия
при смятии материала от прижатия
поверхностей контактов S
внешней силой F
зависит от твердости используемого
материала
 .
Медь является одним из наиболее
распространенных проводниковых
материалов, применяемых для контактов
аппаратов. При применяемых покрытиях
твердых металлов мягкими (меди –
оловом, серебром, стали – кадмием и
цинком)
уменьшается,
а действительная контактная
поверхность увеличивается,
вследствие чего Rперех
падает при том же усилии нажатия.
Величина переходного сопротивления
изменяется в зависимости от удельного
сопротивления
материала контактов, уменьшаясь при
снижении последнего.
- влияние
температуры.
Энергия,
выделяющаяся при прохождении тока
через контактные элементы, частично
превращается в тепловую,
нагревая их в процессе работы и
рассеиваясь в окружающую среду.
Чрезмерный
нагрев контактов
часто приводит к их окислению, причем
оксидные пленки большей части металлов
неэлектропроводны и увеличивают
величину переходного сопротивления.
Единственным материалом, имеющим
оксидную пленку такого же удельного
сопротивления, как и сам металл,
является серебро.
Металлом, вообще не образующим оксидных
пленок, является платина.
С повышением температуры контактов
окисления обычно увеличивается и для
большинства металлов становится
существенным, начиная с температуры
+(70 – 75)0С.
Особенно значительно повышение
температуры контактов при к.з. в цепи.
В условиях к.з. происходит деформация
материала и изменение формы контактов,
снижения их механической прочности
и других свойств. Для ряда аппаратов
размеры контактов определяются
возможностью работы при токах к.з. При
определении предельно допустимой для
аппарата величины тока к.з. длительностью
прохождения тока принимают равной
1,5 или 10 сек. Предельно допустимая
кратковременная температура контактов
при к.з. для контактов из меди –
200-3000С,
для контактов из алюминия – 150-2000С.
- влияние
величины и состояния контактной
поверхности.
.
Медь является одним из наиболее
распространенных проводниковых
материалов, применяемых для контактов
аппаратов. При применяемых покрытиях
твердых металлов мягкими (меди –
оловом, серебром, стали – кадмием и
цинком)
уменьшается,
а действительная контактная
поверхность увеличивается,
вследствие чего Rперех
падает при том же усилии нажатия.
Величина переходного сопротивления
изменяется в зависимости от удельного
сопротивления
материала контактов, уменьшаясь при
снижении последнего.
- влияние
температуры.
Энергия,
выделяющаяся при прохождении тока
через контактные элементы, частично
превращается в тепловую,
нагревая их в процессе работы и
рассеиваясь в окружающую среду.
Чрезмерный
нагрев контактов
часто приводит к их окислению, причем
оксидные пленки большей части металлов
неэлектропроводны и увеличивают
величину переходного сопротивления.
Единственным материалом, имеющим
оксидную пленку такого же удельного
сопротивления, как и сам металл,
является серебро.
Металлом, вообще не образующим оксидных
пленок, является платина.
С повышением температуры контактов
окисления обычно увеличивается и для
большинства металлов становится
существенным, начиная с температуры
+(70 – 75)0С.
Особенно значительно повышение
температуры контактов при к.з. в цепи.
В условиях к.з. происходит деформация
материала и изменение формы контактов,
снижения их механической прочности
и других свойств. Для ряда аппаратов
размеры контактов определяются
возможностью работы при токах к.з. При
определении предельно допустимой для
аппарата величины тока к.з. длительностью
прохождения тока принимают равной
1,5 или 10 сек. Предельно допустимая
кратковременная температура контактов
при к.з. для контактов из меди –
200-3000С,
для контактов из алюминия – 150-2000С.
- влияние
величины и состояния контактной
поверхности. (рис.6.1, а).
Физика такая: в области
x<0
сила, действующая на частицу, ноль,
при x>0
сила, действующая на частицу тоже ноль
(потенциальная энергия постоянна), но
зато в окрестности нуля действует
сила
(рис.6.1, а).
Физика такая: в области
x<0
сила, действующая на частицу, ноль,
при x>0
сила, действующая на частицу тоже ноль
(потенциальная энергия постоянна), но
зато в окрестности нуля действует
сила
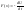 .
График силы изображён на рисунке 6.1,
б.
Для такой ступеньки производная
бесконечно велика, это означает, что
в окрестности нуля действует бесконечно
большая сила, направленная влево, но,
хотя сила бесконечно большая, работа
против этой силы тем не менее конечна.
Наглядно: вот стоит абсолютно твёрдая
стенка, абсолютная твёрдость означает,
что при столкновении со стенкой
отбрасывающая сила бесконечно велика,
но тем не менее стенка пробиваема:
если налетающая частица имеет
кинетическую энергию больше некоторой,
то она эту стенку пробивает. Работа
по преодолению этой силы тем не менее
конечна. Это будет изображаться таким
потенциальным барьером. Реально это
можно реализовать для электронов.
Имеем две металлические стенки, к этим
стенкам приложена разность потенциалов.
Электрон попадает в область электрического
поля между стенками и испытывает силу,
выталкивающую его обратно. Теперь,
выдерживая постоянное напряжение,
будем сближать эти стенки. Напряжённость
электрического поля стремится к
бесконечности, но работа по пробиванию
этого конденсатора остаётся конечной.
Этот барьер для электронов будет
реализован вот таким образом. А теперь
мы будем рассматривать стационарное
состояние. Высота барьера U0,
пишем уравнение Шрёдингера для
стационарных состояний:
.
График силы изображён на рисунке 6.1,
б.
Для такой ступеньки производная
бесконечно велика, это означает, что
в окрестности нуля действует бесконечно
большая сила, направленная влево, но,
хотя сила бесконечно большая, работа
против этой силы тем не менее конечна.
Наглядно: вот стоит абсолютно твёрдая
стенка, абсолютная твёрдость означает,
что при столкновении со стенкой
отбрасывающая сила бесконечно велика,
но тем не менее стенка пробиваема:
если налетающая частица имеет
кинетическую энергию больше некоторой,
то она эту стенку пробивает. Работа
по преодолению этой силы тем не менее
конечна. Это будет изображаться таким
потенциальным барьером. Реально это
можно реализовать для электронов.
Имеем две металлические стенки, к этим
стенкам приложена разность потенциалов.
Электрон попадает в область электрического
поля между стенками и испытывает силу,
выталкивающую его обратно. Теперь,
выдерживая постоянное напряжение,
будем сближать эти стенки. Напряжённость
электрического поля стремится к
бесконечности, но работа по пробиванию
этого конденсатора остаётся конечной.
Этот барьер для электронов будет
реализован вот таким образом. А теперь
мы будем рассматривать стационарное
состояние. Высота барьера U0,
пишем уравнение Шрёдингера для
стационарных состояний:
 Как нам затолкать эту
разрывную функцию U(x)
туда? А просто мы сейчас разделим всё
пространство на две части, напишем
это уравнение для области x<0
и потом напишем это уравнение для
области x>0,
найдём эти решения, а потом их будем
сшивать в точке x0=0,
чтоб получить одну функцию (волновая
функция должна быть непрерывной).
Как нам затолкать эту
разрывную функцию U(x)
туда? А просто мы сейчас разделим всё
пространство на две части, напишем
это уравнение для области x<0
и потом напишем это уравнение для
области x>0,
найдём эти решения, а потом их будем
сшивать в точке x0=0,
чтоб получить одну функцию (волновая
функция должна быть непрерывной). (8.1)
(8.1) (8.2)
(8.2) .
Это решение в области x<0.
.
Это решение в области x<0.
 в случае E>U0
имеет решение такое же как при x<0,
а если
в случае E>U0
имеет решение такое же как при x<0,
а если
 ,
то это уравнение другого типа, оно
имеет другое решение.
,
то это уравнение другого типа, оно
имеет другое решение.
 и E>U0.
и E>U0.
 (8.3)
На волновую функцию
накладывается ещё одно требование –
непрерывность первой производной
(физическую основу этих требований
мы ещё увидим):
(8.3)
На волновую функцию
накладывается ещё одно требование –
непрерывность первой производной
(физическую основу этих требований
мы ещё увидим): (8.4)
(8.4)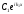 это волна, бегущая вправо вдоль оси
x,
она описывает налетающие частицы,
это волна, бегущая вправо вдоль оси
x,
она описывает налетающие частицы,
 это волна, бегущая влево вдоль оси x
в области x<0,
это волна может быть отразившейся, мы
пока оставим это дело. Константа C1
описывает падающую волну, она
соответствует амплитуде падающей
волны, то есть, в конечном счёте,
интенсивности налетающего пучка,
значит, C1
заданная константа, C2
подлежит определению. Смотрим на
решение u2
в области
это волна, бегущая влево вдоль оси x
в области x<0,
это волна может быть отразившейся, мы
пока оставим это дело. Константа C1
описывает падающую волну, она
соответствует амплитуде падающей
волны, то есть, в конечном счёте,
интенсивности налетающего пучка,
значит, C1
заданная константа, C2
подлежит определению. Смотрим на
решение u2
в области
 :
:
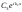 это волна, идущая вправо, она описывает
пучок, прошедший через барьер,
это волна, идущая вправо, она описывает
пучок, прошедший через барьер,
 это волна, идущая влево, физически ей
неоткуда взяться, поэтому полагаем
C4=0.
Теперь мы имеем константу C1
(задаём сами), а C2
и C3
должны определить. У нас есть два
условия, напишем эти условия: формула
(8.3)
в нуле даёт C1+
C2=
C3,
формула (8.4)
даёт
это волна, идущая влево, физически ей
неоткуда взяться, поэтому полагаем
C4=0.
Теперь мы имеем константу C1
(задаём сами), а C2
и C3
должны определить. У нас есть два
условия, напишем эти условия: формула
(8.3)
в нуле даёт C1+
C2=
C3,
формула (8.4)
даёт
 .
Мы
получим:
.
Мы
получим: и
и
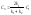
 ,
это означает, что есть отражённая
волна. Квадрат модуля функции даёт
плотность вероятности (вероятность
найти частицу в этой точке), она
пропорциональна количеству частиц.
,
это означает, что есть отражённая
волна. Квадрат модуля функции даёт
плотность вероятности (вероятность
найти частицу в этой точке), она
пропорциональна количеству частиц.
 и E>U0.
Мы нашли, что он проходит барьер, но
существует отличная от нуля вероятность,
что он тем не менее отразится обратно,
потому что в решении появилась
отражённая волна.
и E>U0.
Мы нашли, что он проходит барьер, но
существует отличная от нуля вероятность,
что он тем не менее отразится обратно,
потому что в решении появилась
отражённая волна.
 (235.1)
(235.1) (235.2)
где Ni —
среднее число фермионов в квантовом
состоянии с энергией Еi, —
химический потенциал. В отличие от
(235.1) может
иметь положительное значение (это не
приводит к отрицательным значениям
чисел Ni).
Это распределение называется
распределением Ферми — Дирака. Э.
Ферми (1901—1954) — итальянский физик.
Если
(235.2)
где Ni —
среднее число фермионов в квантовом
состоянии с энергией Еi, —
химический потенциал. В отличие от
(235.1) может
иметь положительное значение (это не
приводит к отрицательным значениям
чисел Ni).
Это распределение называется
распределением Ферми — Дирака. Э.
Ферми (1901—1954) — итальянский физик.
Если  >>1,
то распределения Бозе — Эйнштейна
(235.1) и Ферми — Дирака (235.2) переходят
в классическое распределение Максвелла
— Больцмана:
>>1,
то распределения Бозе — Эйнштейна
(235.1) и Ферми — Дирака (235.2) переходят
в классическое распределение Максвелла
— Больцмана:
 (235.3) (ср. с выражением (44.4)), где
(235.3) (ср. с выражением (44.4)), где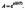 (235.4) Таким образом, при высоких
температурах оба «квантовых» газа
ведут себя подобно классическому
газу. Система частиц называется
вырожденной, если ее свойства
существенным образом отличаются от
свойств систем, подчиняющихся
классической статистике. Поведение
как бозе-газа, так и ферми-газа отличается
от классического газа, они являются
вырожденными газами. Вырождение газов
становится существенным при весьма
низких температурах и больших
плотностях. Параметром вырождения
называется величина А. При А<<1,т.
е. при малой степени вырождения,
распределения Бозе — Эйнштейна (235.1)
и Ферми — Дирака (235.2) переходят в
классическое распределение Максвелла
— Больцмана (235.3). Температурой
вырождения Т0 называется температура,
ниже которой отчетливо проявляются
квантовые свойства идеального газа,
обусловленные тождественностью
частиц, т. е. Т0 — температура, при
которой вырождение становится
существенным. Если Т >> Т0, то поведение
системы частиц (газа) описывается
классическими законами.
(235.4) Таким образом, при высоких
температурах оба «квантовых» газа
ведут себя подобно классическому
газу. Система частиц называется
вырожденной, если ее свойства
существенным образом отличаются от
свойств систем, подчиняющихся
классической статистике. Поведение
как бозе-газа, так и ферми-газа отличается
от классического газа, они являются
вырожденными газами. Вырождение газов
становится существенным при весьма
низких температурах и больших
плотностях. Параметром вырождения
называется величина А. При А<<1,т.
е. при малой степени вырождения,
распределения Бозе — Эйнштейна (235.1)
и Ферми — Дирака (235.2) переходят в
классическое распределение Максвелла
— Больцмана (235.3). Температурой
вырождения Т0 называется температура,
ниже которой отчетливо проявляются
квантовые свойства идеального газа,
обусловленные тождественностью
частиц, т. е. Т0 — температура, при
которой вырождение становится
существенным. Если Т >> Т0, то поведение
системы частиц (газа) описывается
классическими законами.
 ,
в определенный момент времени t она
будет иметь вид
,
в определенный момент времени t она
будет иметь вид  .
В таком случае уравнение Шрёдингера
запишется в виде:
.
В таком случае уравнение Шрёдингера
запишется в виде:
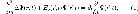
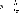 ,
,  — постоянная
Планка;
— постоянная
Планка;  —
масса частицы,
—
масса частицы,  —
внешняя по отношению к частице потенциальная
энергия в точке
—
внешняя по отношению к частице потенциальная
энергия в точке  в
момент времени
в
момент времени  ,
,  — оператор
Лапласа (или лапласиан), в n-мерной
системе координат имеет вид:
— оператор
Лапласа (или лапласиан), в n-мерной
системе координат имеет вид: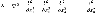
 не
является функцией времени, можно
записать в виде:
не
является функцией времени, можно
записать в виде: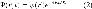
 должна
удовлетворять уравнению:
должна
удовлетворять уравнению:
 (2).
(2).
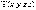 .
Эту величину называют также волновой
функцией (или
.
Эту величину называют также волновой
функцией (или -функцией).
Амплитуда вероятности может быть
комплексной, и вероятность W
пропорциональна квадрату ее модуля:
-функцией).
Амплитуда вероятности может быть
комплексной, и вероятность W
пропорциональна квадрату ее модуля:
 Таким образом, описание состояния
микрообъекта с помощью волновой
функции имеет статистический,
вероятностный характер: квадрат модуля
волновой функции (квадрат модуля
амплитуды волн де Бройля) определяет
вероятность нахождения частицы в
момент времени t в области с координатами
х и х + dx, у и у + dy. : и z + dz. Итак, в
квантовой механике состояние микрочастиц
описывается принципиально по-новому
— с помощью волновой функции, которая
является основным носителем информации
об их корпускулярных и волновых
свойствах. Вероятность нахождения
частицы в элементе объема dV равна:
Таким образом, описание состояния
микрообъекта с помощью волновой
функции имеет статистический,
вероятностный характер: квадрат модуля
волновой функции (квадрат модуля
амплитуды волн де Бройля) определяет
вероятность нахождения частицы в
момент времени t в области с координатами
х и х + dx, у и у + dy. : и z + dz. Итак, в
квантовой механике состояние микрочастиц
описывается принципиально по-новому
— с помощью волновой функции, которая
является основным носителем информации
об их корпускулярных и волновых
свойствах. Вероятность нахождения
частицы в элементе объема dV равна:
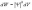 где величина
где величина
 (квадрат модуля Т-функции) имеет смысл
плотности вероятности. Таким образом,
физический смысл имеет не сама
(квадрат модуля Т-функции) имеет смысл
плотности вероятности. Таким образом,
физический смысл имеет не сама
 -функция,
а квадрат ее модуля
-функция,
а квадрат ее модуля
 (
( -функция,
комплексно-сопряженная с
-функция,
комплексно-сопряженная с
 ),
которым определяется интенсивность
волн де Бройля.
),
которым определяется интенсивность
волн де Бройля. Поскольку
Поскольку
 определяется как вероятность, необходимо
волновую функцию Т нормировать так,
чтобы вероятность W достоверного
события обращалась в единицу, если за
объем V принять бесконечный объем
всего пространства. Это означает, что
при данном условии частица должна
находиться где-то в пространстве.
Следовательно, условие нормировки
вероятностей
определяется как вероятность, необходимо
волновую функцию Т нормировать так,
чтобы вероятность W достоверного
события обращалась в единицу, если за
объем V принять бесконечный объем
всего пространства. Это означает, что
при данном условии частица должна
находиться где-то в пространстве.
Следовательно, условие нормировки
вероятностей
 где тройной интеграл вычисляется по
всему бесконечному пространству, т.
е. по координатам х, у. z от минус
бесконечности до плюс бесконечности
. Таким образом, условие говорит об
объективном существовании частицы
во времени и пространстве.
Свойства:
Чтобы волновая функция являлась
объективной характеристикой состояния
микрочастиц, она должна удовлетворять
ряду ограничительных условий. Функция
Т, характеризуя вероятность обнаружения
действия микрочастицы в элементе
объема, должна быть конечной (вероятность
не может быть больше единицы), однозначной
(вероятность не может быть не однозначной
величиной) и непрерывной (вероятность
не может изменяться скачком).
где тройной интеграл вычисляется по
всему бесконечному пространству, т.
е. по координатам х, у. z от минус
бесконечности до плюс бесконечности
. Таким образом, условие говорит об
объективном существовании частицы
во времени и пространстве.
Свойства:
Чтобы волновая функция являлась
объективной характеристикой состояния
микрочастиц, она должна удовлетворять
ряду ограничительных условий. Функция
Т, характеризуя вероятность обнаружения
действия микрочастицы в элементе
объема, должна быть конечной (вероятность
не может быть больше единицы), однозначной
(вероятность не может быть не однозначной
величиной) и непрерывной (вероятность
не может изменяться скачком). то она также может находиться в
состоянии
то она также может находиться в
состоянии
 ,
описываемом линейной комбинацией
этих функций:
,
описываемом линейной комбинацией
этих функций:
 где
Сn (n = 1,2,…) — некоторые комплексные
числа. Сложение волновых функций
(амплитуд вероятностей), а не вероятностей
(квадратов волновых функций) принципиально
отличает квантовую теорию от классической
статистической теории, в которой для
независимых событий справедлива
теорема сложения вероятностей. Зная
волновую функцию
где
Сn (n = 1,2,…) — некоторые комплексные
числа. Сложение волновых функций
(амплитуд вероятностей), а не вероятностей
(квадратов волновых функций) принципиально
отличает квантовую теорию от классической
статистической теории, в которой для
независимых событий справедлива
теорема сложения вероятностей. Зная
волновую функцию
 в квантовой механике, вычисляют
средние значения физических величин,
характеризующих данный микрообъект.
Например, среднее расстояние <r>
электрона от ядра вычисляют по
формуле:
в квантовой механике, вычисляют
средние значения физических величин,
характеризующих данный микрообъект.
Например, среднее расстояние <r>
электрона от ядра вычисляют по
формуле:
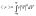 где интегрирование производится, как
и в случае выше. Уравнение
Шредингера
Статистическое толкование волн де
Бройля и соотношение неопределенностей
Гейзенберга привели к выводу, что
уравнением движения в квантовой
механике, описывающим движение
микрочастиц в различных силовых полях,
должно быть уравнение, из которого
бы вытекали наблюдаемые на опыте
волновые свойства частиц. Основное
уравнение должно быть уравнением
относительно волновой функции
где интегрирование производится, как
и в случае выше. Уравнение
Шредингера
Статистическое толкование волн де
Бройля и соотношение неопределенностей
Гейзенберга привели к выводу, что
уравнением движения в квантовой
механике, описывающим движение
микрочастиц в различных силовых полях,
должно быть уравнение, из которого
бы вытекали наблюдаемые на опыте
волновые свойства частиц. Основное
уравнение должно быть уравнением
относительно волновой функции
 ,
так как именно она, или, точнее, величина
,
так как именно она, или, точнее, величина
 ,
определяет вероятность пребывания
частицы в момент времени t в объеме
,
определяет вероятность пребывания
частицы в момент времени t в объеме
 ,
т. е. в области с координатами х и x+dx,
у и у+dy, z и z + dz. Так как искомое уравнение
должно учитывать волновые свойства
частиц, то оно должно быть волновым
уравнением, подобно уравнению,
описывающему электромагнитные волны.
Основное уравнение нерелятивистской
квантовой механики сформулировано
Э. Шредингером (1926). Уравнение Шредингера,
как и все основные уравнения физики
(например, уравнение Ньютона в
классической механике и уравнения
Максвелла для электромагнитного
поля), не выводится, а постулируется.
Правильность этого уравнения
подтверждается согласием с опытом
получаемых с его помощью результатов,
что, в свою очередь, придает ему характер
закона природы. Уравнение Шредингера
имеет вид
,
т. е. в области с координатами х и x+dx,
у и у+dy, z и z + dz. Так как искомое уравнение
должно учитывать волновые свойства
частиц, то оно должно быть волновым
уравнением, подобно уравнению,
описывающему электромагнитные волны.
Основное уравнение нерелятивистской
квантовой механики сформулировано
Э. Шредингером (1926). Уравнение Шредингера,
как и все основные уравнения физики
(например, уравнение Ньютона в
классической механике и уравнения
Максвелла для электромагнитного
поля), не выводится, а постулируется.
Правильность этого уравнения
подтверждается согласием с опытом
получаемых с его помощью результатов,
что, в свою очередь, придает ему характер
закона природы. Уравнение Шредингера
имеет вид
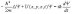 (7.1) где
(7.1) где
 ,
m – масса частицы,
,
m – масса частицы,
 – оператор Лапласа
– оператор Лапласа
 ,
i – мнимая единица,
,
i – мнимая единица,
 - потенциальная энергия частицы в
силовом поле, в котором частица
движется.
- потенциальная энергия частицы в
силовом поле, в котором частица
движется. ,
где
А – массовое число; Z – атомный номер
химического элемента; N – число
нейтронов.
Следовательно,
N
+ Z = A.
Ядра
с одинаковыми величинами А, но разным
Z называются изобарами.
Пример триады изобаров: аргон
,
где
А – массовое число; Z – атомный номер
химического элемента; N – число
нейтронов.
Следовательно,
N
+ Z = A.
Ядра
с одинаковыми величинами А, но разным
Z называются изобарами.
Пример триады изобаров: аргон  ,
калий
,
калий  ,
кальций
,
кальций  .
Нуклиды –
группы атомов с одинаковыми значениями
А и Z. Радиоактивные нуклиды
называются радионуклидами.
Альфа-излучение
– поток
ядер гелия или, иначе, α-частиц.
Альфа-частица состоит из двух
протонов p и
двух нейтронов n:
.
Нуклиды –
группы атомов с одинаковыми значениями
А и Z. Радиоактивные нуклиды
называются радионуклидами.
Альфа-излучение
– поток
ядер гелия или, иначе, α-частиц.
Альфа-частица состоит из двух
протонов p и
двух нейтронов n:
 .
Следовательно,
электрический
заряд α-частицы равен двум элементарным
электрическим зарядам со знаком
(+);
масса равна 4 атомным единицам
массы (масса этих частиц превышает
массу электрона в 7300
раз);Бета-излучение представляет
собой поток электронов или позитронов
ядерного происхождения. Позитрон –
элементарная частица, подобная электрону,
но с положительным знаком заряда
(античастица электрона). Физические
параметры электронов ядерного
происхождения (масса, заряд) такие же,
как и у электронов атомной оболочки.
Обозначаются бета-частицы
символами β- или е-, β+ или е+.
Гамма-излучение –
это поток квантов электромагнитной
энергии (волн) высокой частоты
.Физическая природа этих волн такая
же, как и у радиоволн, видимого света,
ультрафиолетовых и инфракрасных
лучей, рентгеновского излучения.
.
Следовательно,
электрический
заряд α-частицы равен двум элементарным
электрическим зарядам со знаком
(+);
масса равна 4 атомным единицам
массы (масса этих частиц превышает
массу электрона в 7300
раз);Бета-излучение представляет
собой поток электронов или позитронов
ядерного происхождения. Позитрон –
элементарная частица, подобная электрону,
но с положительным знаком заряда
(античастица электрона). Физические
параметры электронов ядерного
происхождения (масса, заряд) такие же,
как и у электронов атомной оболочки.
Обозначаются бета-частицы
символами β- или е-, β+ или е+.
Гамма-излучение –
это поток квантов электромагнитной
энергии (волн) высокой частоты
.Физическая природа этих волн такая
же, как и у радиоволн, видимого света,
ультрафиолетовых и инфракрасных
лучей, рентгеновского излучения.