
Уравнения с разделяющимися переменными
Дифференциальное уравнение вида
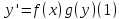
называется уравнением с разделяющимися переменными. Метод решения этого уравнения следующий:
а)
записываем производную
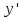 в дифференциалах:
в дифференциалах:
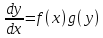 ;
;
б)
разделяем переменные и получаем
уравнение в дифференциалах :
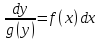 ;
;
в)
интегрируем уравнение в дифференциалах:
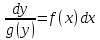 (константуC
записываем лишь одну) -- получаем общее
решение в неявном виде;
(константуC
записываем лишь одну) -- получаем общее
решение в неявном виде;
г) выражаем y через x и C -- получаем общее решение в явном виде.
Заметим, что такой же метод решения применим и дифференциальному уравнению в дифференциалах, имеющему вид
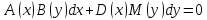
Однородные уравнения
Так называются уравнения вида
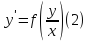
Метод решения: а)
переходим к новой неизвестной функции
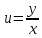 .
Тогда
.
Тогда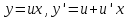 и уравнение (2) переписывается так:
и уравнение (2) переписывается так: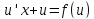 (*). А это уравнение с разделяющимися
переменными.
(*). А это уравнение с разделяющимися
переменными.
б)
Решаем вспомогательное уравнение (*).
Пусть
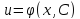 есть его общее решение.
есть его общее решение.
в)
Тогда
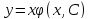 -- общее решение исходного уравнения.
-- общее решение исходного уравнения.
Линейные дифференциальные уравнения 1-го порядка. Уравнения Бернулли.
Так называются уравнения вида
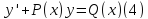
Если P(x), Q(x) непрерывны, то условия теоремы существования и единственности выполнены.
Метод решения
а) Решаем сначала
уравнение
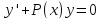 без правой части как уравнение с
разделяющимися переменными. Получаем
общее решение в видеy(x)=C
u(x),
где
без правой части как уравнение с
разделяющимися переменными. Получаем
общее решение в видеy(x)=C
u(x),
где
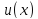 -- одна из первообразных функции
-- одна из первообразных функции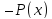 .
.
б) Общее решение уравнения (4) ищем в виде y=C(x)u(x), где C(x) -- функция, подлежащая определению. Такой приём называется методом вариации постоянных.
в) Подставляя
 в (4), имеем:
в (4), имеем:
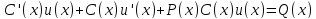
Второе и третье
слагаемые в левой части дают 0, ибо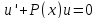 .
Отсюда
.
Отсюда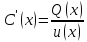
г) Решая это уравнение, т.е. интегрируя, находим
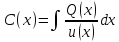
д) Подставляя это
в
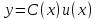 ,
получаем общее решение исходного
уравнения.
,
получаем общее решение исходного
уравнения.
Обыкновенное дифференциальное уравнение вида:
![]()
называется уравнением
Бернулли (при ![]() или
или![]() получаем
неоднородное или однородное линейное
уравнение).
получаем
неоднородное или однородное линейное
уравнение).
Заменим
![]()
тогда:
![]()
Подберем ![]() так,
чтобы было
так,
чтобы было
![]()
для
этого достаточно решить уравнение с
разделяющимися переменными 1-го порядка.
После этого для определения ![]() получаем
уравнение
получаем
уравнение![]() —
уравнение с разделяющимися переменными.
—
уравнение с разделяющимися переменными.
Уравнения в полных дифференциалах.
Дифференциальное уравнение вида
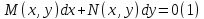
называется
уравнением в дифференциалах. Заметим,
что (1) действительно дифференциальное
уравнение первого порядка, ибо оно
может быть переписано для области D,
в которой N(x,y)≠
0 как
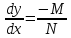 .
.
Уравнение (1)
назовём уравнением в полных дифференциалах,
если в рассматриваемой области существует
функция
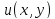 ,
называемая потенциалом, дифференциал
которой равен левой части уравнения,
т.е.
,
называемая потенциалом, дифференциал
которой равен левой части уравнения,
т.е.
Уравнение в полных дифференциалах может быть переписано в виде du(x,y)=0 общим решением которого являются эквипотенциальные кривые, задаваемые соотношением u(x,y)=C.
Теорема.
Пусть
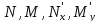 непрерывны в некоторой односвязной
областиD.
Тогда (1) будет уравнением в полных
дифференциалах в том и только том
случае, когда в этой области выполнено
условие
непрерывны в некоторой односвязной
областиD.
Тогда (1) будет уравнением в полных
дифференциалах в том и только том
случае, когда в этой области выполнено
условие
Неполные уравнения высших порядков.
Линейные дифференциальные уравнения; однородные и неоднородные. Линейность пространства решений однородного линейного уравнения. Общее решение неоднородного линейного дифференциального уравнения.
Дифференциальное уравнение вида
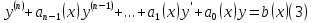
называют линейным неоднородным уравнением или линейным уравнением с правой частью. Если правая часть равна нулю, т.е. если уравнение имеет вид
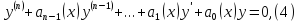
то его называют
линейным однородным уравнением.
Заметим, что для существования и
единственности решения задачи Коши
достаточно потребовать непрерывности
функций
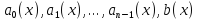 .
Непрерывность этих функций в дальнейшем
предполагается и особо не оговаривается.
.
Непрерывность этих функций в дальнейшем
предполагается и особо не оговаривается.
В частности дифференциальные линейные уравнения (неоднородное и однородное) второго порядка имеют вид:
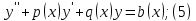
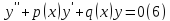
Теорема 1. Сумма двух решений уравнения (6) снова будет решением, и произведение решения на число также будет решением.
Теорема 2.
Пусть
 -- общее решение однородного уравнения
(6), а
-- общее решение однородного уравнения
(6), а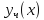 -- частное решение неоднородного
уравнения (5). Тогда
-- частное решение неоднородного
уравнения (5). Тогда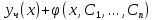 есть общее решение неоднородного
уравнения (5).
есть общее решение неоднородного
уравнения (5).
Основная теорема
о структуре пространства решений
однородного линейного дифференциального
уравнения.
Пусть
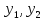 —не
пропорциональные решения. однородного
линейного дифференциального уравнения
2-го порядка. Тогда
—не
пропорциональные решения. однородного
линейного дифференциального уравнения
2-го порядка. Тогда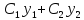 есть общее решение этого уравнения.
есть общее решение этого уравнения.
Определитель Вронского. Формула Лиувилля. Основное свойство определителя Вронского. Основная теорема о структуре пространства решений однородного линейного дифференциального уравнения.
Линейное однородное уравнение второго порядка с переменными коэффициентами записывается в виде
![]()
где a1(x) и a2(x) являются непрерывными функциями на отрезке [a,b].
![]()
линейно независимые. Пусть n функций y1(x), y2(x), ..., yn(x) имеют производные (n − 1) порядка. Определитель
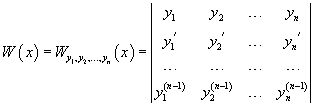
называется определителем Вронского. Теорема. Если система функций y1(x), y2(x), ..., yn(x) линейна зависима на отрезке [a,b], то ее определитель Вронского тождественно равен нулю на этом отрезке. Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка [a,b], то функции y1(x),y2(x), ..., yn(x) будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.Формула Лиувилля-Остроградского
Формула Лиувилля устанавливает связь между вронскианом W(x), построенном на базе частных решений y1(x), y2(x), и коэффициентом a1(x) в дифференциальном уравнении. Пусть W(x) − определитель Вронского решений y1(x), y2(x) линейного однородного дифференциального уравнения 2-го порядка
![]()
в
котором функции a1(x) и a2(x) непрерывны
на отрезке [a,b].
Пусть точка x0 принадлежит
отрезку [a,b].
Тогда для всех ![]() справедливаформула
Лиувилля:
справедливаформула
Лиувилля:
![]()
Основная
теорема о структуре пространства
решений однородного линейного
дифференциального уравнения.
Пусть
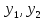 —не
пропорциональные решения однородного
линейного дифференциального уравнения
2-го порядка. Тогда
—не
пропорциональные решения однородного
линейного дифференциального уравнения
2-го порядка. Тогда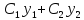 есть общее решение этого уравнения.
есть общее решение этого уравнения.
Решение однородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами.
Решим дифференциальное линейное однородное уравнение второго порядка с постоянными коэффициентами:
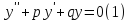
(Здесь
p
и q
– числа). Ищем решение в виде
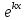 .
Эта функция будет решением (1) тогда и
только тогда, когда
.
Эта функция будет решением (1) тогда и
только тогда, когда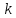 – корень уравнения
– корень уравнения
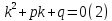
Уравнение (2) называется характеристическим.
Случай
1.
 .
.
Тогда
уравнение (2) имеет два различных
действительных корня
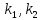 и
и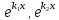 будет Ф.С.Р. уравнения (1). Тем самым
будет Ф.С.Р. уравнения (1). Тем самым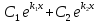 -- общее решение дифференциального
уравнения (1).
-- общее решение дифференциального
уравнения (1).
Случай 2. D=0.
Тогда
характеристическое уравнение (2) имеет
один корень
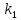 и при этом
и при этом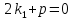 . Подставляя в (1) функцию
. Подставляя в (1) функцию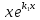 ,
что
,
что
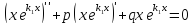
и
тем самым
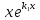 также будет решением, не пропорциональным
решению
также будет решением, не пропорциональным
решению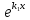 ,
Следовательно, общее решение уравнения
(1) имеет вид
,
Следовательно, общее решение уравнения
(1) имеет вид
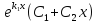
Случай
3. D<0.
Тогда характеристическое уравнение
(2) имеет два комплексно сопряженных
решения
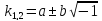 (
(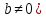 .
Можно проверить, что
.
Можно проверить, что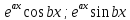 -- два непропорциональных решения
уравнения(1). Отсюда
-- два непропорциональных решения
уравнения(1). Отсюда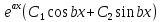 -- общее решение.
-- общее решение.
Метод подбора решения неоднородного линейного дифференциального уравнения
Решаем уравнение
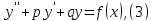
где правая часть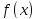 имеет специальный вид, а
имеет специальный вид, а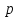 и
и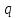 по-прежнему суть числа. Мы применяем
теорему, согласно которой общее решение
уравнения (3) есть сумма общего решения
однородного уравнения
по-прежнему суть числа. Мы применяем
теорему, согласно которой общее решение
уравнения (3) есть сумма общего решения
однородного уравнения
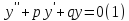
и
частного решения (обозначим его
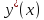 )
уравнения (3). Так как общее решение
однородного уравнения мы научились
находить, то осталось выяснить в каком
виде и как находится какое-либо частное
решение неоднородного уравнения (3).
)
уравнения (3). Так как общее решение
однородного уравнения мы научились
находить, то осталось выяснить в каком
виде и как находится какое-либо частное
решение неоднородного уравнения (3).
Предположим, что
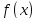 есть функция вида
есть функция вида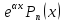 (здесь
(здесь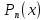 – многочлен степениn).
– многочлен степениn).
Случай а) Число
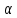 не является корнем характеристического
уравнения (2).
не является корнем характеристического
уравнения (2).
Тогда
частное решение можно найти в виде
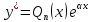 ,
где
,
где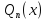 -- многочлен степениn.
-- многочлен степениn.
Случай б). Число
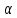 совпадает ровно с одним корнем
характеристического уравнения
совпадает ровно с одним корнем
характеристического уравнения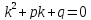 .
.
Тогда
частное решение можно найти в виде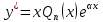 ,
где
,
где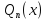 -- многочлен степениn.
Приравнивая коэффициенты при одинаковых
степенях, после подстановки
-- многочлен степениn.
Приравнивая коэффициенты при одинаковых
степенях, после подстановки
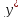 в уравнение
(3), находим коэффициенты многочлена
в уравнение
(3), находим коэффициенты многочлена
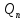 .
.
Случай
в). Число
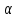 -- двукратный корень характеристического
уравнения.
-- двукратный корень характеристического
уравнения.
Тогда
частное решение можно найти в виде
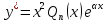 ,
где
,
где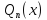 -- многочлен степениn,
-- многочлен степениn,
Подведем
итог и сформулируем вид частного
решения, применимый сразу для всех трех
случаев а), б), в). Для этого определим
число
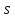 – кратность показателя
– кратность показателя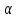 в характеристическом уравнении – число
корней (2), с которыми совпадает
в характеристическом уравнении – число
корней (2), с которыми совпадает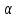 .
По другому, это наибольшее неотрицательное
целое число, такое, что
.
По другому, это наибольшее неотрицательное
целое число, такое, что делит
делит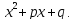 Возможные значения суть 0, 1 или 2.
Возможные значения суть 0, 1 или 2.
Метод вариации постоянных решения неоднородного линейного дифференциального уравнения.
Решаем неоднородное линейное уравнение
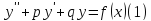
вообще говоря с
переменными коэффициентами. Предположим,
что нам удалось найти Ф.С.Р. однородного
уравнения
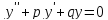 , тогда общее решение этого уравнения
будет
, тогда общее решение этого уравнения
будет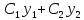 .
.
Решение уравнения
(1) ищем в виде
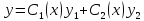 ,
где
,
где неизвестные функции, подлежащие
определению. Имеем
неизвестные функции, подлежащие
определению. Имеем
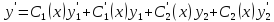
Положим
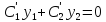 (*). Тогда, с учетом этого, вычислим вторую
производную:
(*). Тогда, с учетом этого, вычислим вторую
производную:

Подставляя
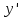 и
и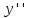 в (1), получим
в (1), получим
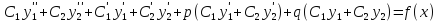
Так как
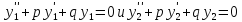 ,
то приходим к уравнению
,
то приходим к уравнению
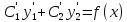
Вместе с (*),
получаем систему, из которой находятся
функции
 интегрированием:
интегрированием:
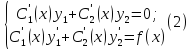
Метод вариации постоянных
Пример 1
Найти
общее решение дифференциального
уравнения ![]() (Диффур
из Примера №2 урока Линейные
неоднородные ДУ 1-го порядка)
(Диффур
из Примера №2 урока Линейные
неоднородные ДУ 1-го порядка)
Решение: Данное
уравнение является линейным неоднородным
и имеет знакомый вид:
![]()
На
первом этапе необходимо решить более
простое уравнение: ![]() То
есть, тупо обнуляем правую часть –
вместо
То
есть, тупо обнуляем правую часть –
вместо ![]() пишем
ноль.
Уравнение
пишем
ноль.
Уравнение ![]() я
буду называть вспомогательным
уравнением.
я
буду называть вспомогательным
уравнением.
В
данном примере нужно решить следующее
вспомогательное уравнение:
![]()
Перед
нами уравнение
с разделяющимися переменными,
решение которого (надеюсь) уже не
представляет для вас сложностей:
![]()
Таким
образом:
![]() –
общее решение вспомогательного
уравнения
–
общее решение вспомогательного
уравнения ![]() .
.
На
втором шаге заменим константу ![]() некоторой пока
ещё неизвестной
функцией
некоторой пока
ещё неизвестной
функцией ![]() ,
которая зависит от «икс»:
,
которая зависит от «икс»:
![]()
Отсюда
и название метода – варьируем константу ![]() .
Как вариант, константа
.
Как вариант, константа ![]() может
быть некоторой функцией
может
быть некоторой функцией ![]() ,
которую нам предстоит сейчас найти.
,
которую нам предстоит сейчас найти.
В исходном неоднородном
уравнении ![]() проведём
замену:
проведём
замену:
![]()
По
правилу дифференцирования произведения:
![]()
Подставим ![]() и
и ![]() в
уравнение
в
уравнение ![]() :
:
![]()
Контрольный момент – два слагаемых в левой части сокращаются. Если этого не происходит, следует искать ошибку выше.
![]()
В результате замены получено уравнение с разделяющимися переменными. Разделяем переменные и интегрируем.
Какая
благодать, экспоненты тоже сокращаются:
![]()
К
найденной функции ![]() приплюсовываем
«нормальную» константу
приплюсовываем
«нормальную» константу ![]() :
:
![]()
На
заключительном этапе вспоминаем про
нашу замену: ![]()
Функция ![]() только
что найдена!
только
что найдена!
Таким
образом, общее решение:
![]()
Ответ: общее
решение:![]()
Линейные системы дифференциальных уравнений. Решение линейной системы с постоянными коэффициентами.
Система обыкновенных дифференциальных уравнений вида
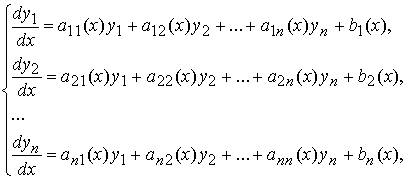
где aij(x) и bi (x) — известные, а yj (x) — неизвестные функции, (i = 1,2, … ,n, j = 1,2, … , n) называется линейной системой дифференциальных уравнений.
При описании линейных систем дифференциальных уравнений удобнее пользоваться векторной (матричной) формой записи. Обозначим
![]()
Тогда линейная система дифференциальных уравнений в векторной (матричной) форме записывается в виде Y' = A(x)Y + b(x) или, что то же самое, в виде
![]()
Матрица A называется матрицей системы, а вектор–функция b(x) — неоднородностью системы.
Система Y' = A(x)Y + b(x) называется неоднородной линейной системой дифференциальных уравнений, а система Y' = A(x)Y— однороднойлинейной системой.
Справедлива следующая теорема существования и единственности решения задачи Коши для линейной системы дифференциальных уравнений.
Если A(x) и b(x) непрерывны на отрезке [a, b] , то какова бы ни была начальная точка (x0, Y0) из Rn + 1, задача Коши Y' = A(x)Y + b(x), Y(x0) = Y0,
имеет единственное на [a,b] решение Y = Y(x) .
Важно отметить, что для линейной системы дифференциальных уравнений разрешимость задачи Коши глобальная: решение существует всюду, где непрерывны коэффициенты и неоднородность системы.
