
- •Теоретические основы электротехники. Теория электромагнитного поля Abstract
- •Введение
- •1. Основные понятия теории электромагнитного поля
- •1.1. Определение электромагнитного поля. Математический аппарат теории электромагнитного поля
- •1.2. Физические величины, характеризующие эмп
- •В соответствии с этим определением электрическая сила, действующая на точечный заряд q равна: , где e измеряется в в/м.
- •1.3. Источники электромагнитного поля
- •Пример применения matlab
- •1.4. Пространственные дифференциальные операторы в теории электромагнитного поля
- •Пример применения matlab
- •1.5. Основные законы теории электромагнитного поля Уравнения эмп в интегральной форме
- •Уравнения Максвелла для неподвижных сред
- •Соотношения между векторами поля и электрофизическими свойствами среды
- •Энергия электромагнитного поля
- •Примеры применения matlab
- •1.6. Граничные условия для векторов эмп. Закон сохранения заряда. Теорема Умова-Пойнтинга Граничные условия для векторов эмп
- •Закон сохранения заряда
- •Граничные условия для плотности тока
- •Теорема Умова-Пойнтинга
- •Пример применения matlab
- •2. Электростатическое поле
- •2.1. Основные уравнения электростатики
- •Граничные условия для векторов электростатического поля
- •Скалярный электрический потенциал. Краевая задача анализа электростатического поля
- •Если в расчетной области свободные заряды отсутствуют, то
- •Скалярная краевая задача электростатики в пакетах расширения matlab
- •Энергия системы заряженных проводников
- •Понятие о методе изображений
- •Фундаментальное решение уравнений Пуассона и Лапласа
- •2.2. Электростатические поля простых геометрических форм Поле электрического диполя
- •В результате получим
- •Окончательно получим
- •Расчёт и визуализация поля электрического диполя в системе matlab
- •Поле бесконечно длинной заряженной оси
- •2.3. Электростатические поля простых двухпроводных линий Поле двух разноименно заряженных осей
- •Поле и емкость параллельных цилиндров с несовпадающими осями
- •Поле и емкость системы цилиндр – плоскость
- •Поле и ёмкость двухпроводной линии
- •Поле и емкость двухпроводной линии с учетом влияния Земли
- •Систему уравнений (2) можно записать иначе
- •2.4. Распределение зарядов и потенциалов в системе заряженных проводников
- •3.2. Граничные условия для векторов электрического поля постоянного тока
- •3.3. Аналогия между электрическим полем постоянного тока в проводнике и электростатическим полем в диэлектрике
- •3.4. Электрическое поле в диэлектрике вблизи проводника с током
- •3.5. Электрическое поле в несовершенных изолирующих средах
- •3.6. Электрическое моделирование физических полей
- •4. Магнитостатическое поле
- •4.1. Основные законы магнитостатики Уравнения магнитостатического поля в интегральной и дифференциальной формах
- •Граничные условия для векторов магнитного поля
- •Векторные уравнения Пуассона и Лапласа
- •Краевая задача магнитостатики для неоднородных сред
- •Магнитное поле элемента тока
- •4.2. Интегральные параметры магнитостатического поля
- •Потокосцепление. Собственная и взаимная индуктивности
- •Вычисление взаимной индуктивности круглых и прямоугольных контуров в системе matlab
- •4.3. Частные случаи плоскопараллельных магнитных полей постоянных токов Распределение векторного потенциала в случае одиночного провода круглого сечения
- •Магнитное поле и индуктивность двухпроводной линии
- •Магнитное поле и индуктивность коаксиального кабеля
- •4.4. Магнитное поле цилиндрической катушки
- •Расчёт распределения напряжённости магнитного поля на оси многослойной цилиндрической катушки в системе matlab
- •4.5. Скалярная краевая задача анализа магнитостатического поля
- •4.6. Магнитное экранирование
- •4.7. Пространственные интегральные уравнения в магнитостатике
- •4.8. Мощность, передаваемая по двухпроводной линии постоянного тока
- •5. Переменное гармоническое электромагнитное поле
- •5.1. Основные уравнения электромагнитного поля в комплексной форме Гармоническое электромагнитное поле. Основные понятия и определения
- •Уравнения Максвелла в комплексной форме
- •Теорема Умова-Пойнтинга в комплексной форме
- •Используя соотношения (3) и (4), можно доказать, что
- •Теорема о единственности
- •5.2. Уравнения математической физики относительно потенциалов гармонического электромагнитного поля Комплексные параметры электрофизических свойств среды
- •Системы электродинамических потенциалов и уравнения математической физики для гармонического электромагнитного поля
- •Излучатель Герца
- •Элементарный магнитный излучатель
- •5.3. Частные приложения теории гармонического электромагнитного поля Понятие о поверхностном эффекте и эффекте близости
- •Плоская волна в однородном проводнике
- •Поверхностный эффект в проводящей пластине
- •Поверхностный эффект в круглом проводе
- •Заключение
2.4. Распределение зарядов и потенциалов в системе заряженных проводников
Пусть
имеется система из n
заряженных проводников: qi
(i
=
1,…, n
) – заряды проводников,
![]() (i
= 1,…, n
) – потенциалы проводников.
(i
= 1,…, n
) – потенциалы проводников.
Потенциалы проводников можно представить в виде линейной комбинации их зарядов.
![]() ;
;
или
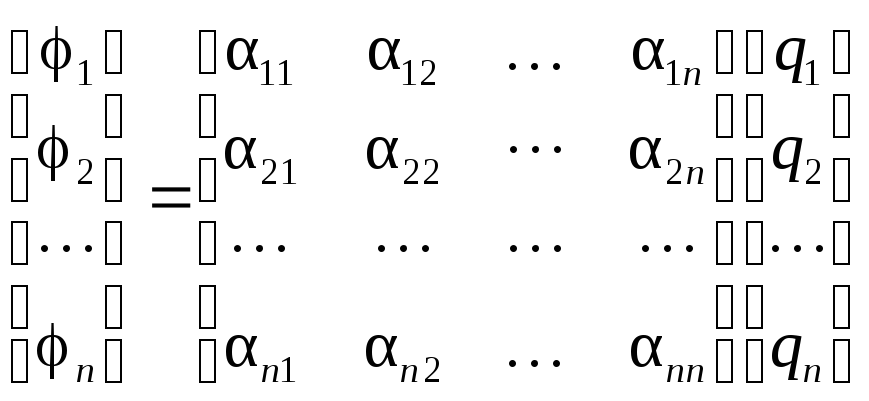
или
![]()
Коэффициенты
![]() называются потенциальными коэффициентами
системы проводников и измеряются в 1/Ф.
называются потенциальными коэффициентами
системы проводников и измеряются в 1/Ф.
Из последнего матричного уравнения можно выразить заряды проводников
![]()
или
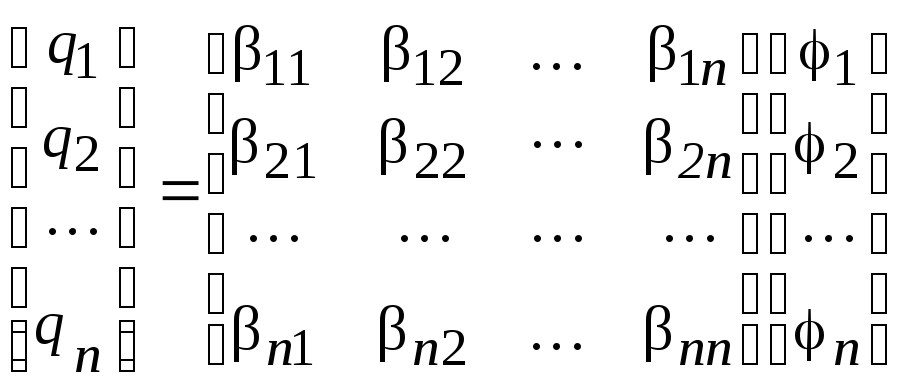 ,
,
т.
е.
![]() .
.
Коэффициенты
![]() называются емкостными коэффициентами
системы проводников и измеряются в Ф.
называются емкостными коэффициентами
системы проводников и измеряются в Ф.
Последнее соотношение можно записать иначе
![]() ;
;
Сij – это частичные емкости системы проводников;
![]() –собственные
частичные емкости;
–собственные
частичные емкости;
![]() –взаимные
частичные емкости.
–взаимные
частичные емкости.
Матрицы
![]() симметричные, т.е.
симметричные, т.е.![]() .
Значит, для системы заряженных проводников
выполняется принцип взаимности.
.
Значит, для системы заряженных проводников
выполняется принцип взаимности.
2.5 Электростатические экраны
Принцип электростатического экранирования электрических и электронных элементов в аппаратуре основан на том, что медленно изменяющееся электрическое поле не может проникнуть внутрь объема, ограниченного проводником, поскольку любая поверхность электропроводящего тела в электростатическом поле является эквипотенциальной.
3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ПОСТОЯННОГО ТОКА В ПРОВОДЯЩЕЙ СРЕДЕ
3.1. Законы электрического поля в проводящей среде
Электрическое поле в проводящей среде характеризуется пространственным распределением вектора напряженности электрического поля и вектора плотности тока.
Уравнения электрического поля в дифференциальной форме имеют вид:
![]() (3.1.1)
(3.1.1)
![]() (3.1.2)
(3.1.2)
![]() (3.1.3)
(3.1.3)
Уравнение (3.1.1) называют вторым законом Кирхгофа в дифференциальной форме. Уравнение (3.1.2) называют первым законом Кирхгофа в дифференциальной форме. Уравнение (3.1.3) называют законом Ома в дифференциальной форме.
При
составлении математических моделей
электрического поля в проводящей среде
источником векторного поля E
можно считать пространственное
распределение вектора сторонней
напряженности электрического поля Eс
(объемно-распределенные источники ЭДС);
источником векторного поля плотности
тока проводимости
![]() можно считать пространственное
распределение вектора сторонней
плотности тока
можно считать пространственное
распределение вектора сторонней
плотности тока![]() (объёмно-распредёленные источники тока,
единица измерения – А/м2),
а также объёмной плотности тока внешних
источников J
(единица измерения – А/м3).
Здесь под внешними источниками тока
понимаются известные токи, закачиваемые
в моделируемую систему извне.
(объёмно-распредёленные источники тока,
единица измерения – А/м2),
а также объёмной плотности тока внешних
источников J
(единица измерения – А/м3).
Здесь под внешними источниками тока
понимаются известные токи, закачиваемые
в моделируемую систему извне.
3.2. Граничные условия для векторов электрического поля постоянного тока
На
поверхности раздела сред, где
![]() ,Eс
или
,Eс
или
![]() изменяются скачком, справедливы следующие
соотношения:
изменяются скачком, справедливы следующие
соотношения:
E1t – E2t = E1сt – E2сt
т.е. скачок тангенциальной составляющей вектора напряженности электрического поля равен скачку сторонней тангенциальной составляющей вектора напряженности электрического поля. Если Eс = 0, то тангенциальная составляющая векторного поля E непрерывна на любой поверхности раздела сред.
![]()
т.е.
скачок нормальной составляющей плотности
тока проводимости равен скачку нормальной
составляющей сторонней плотности тока
с противоположным знаком. Если
![]() = 0, то нормальная составляющая плотности
тока проводимости непрерывна на любой
поверхности раздела сред.
= 0, то нормальная составляющая плотности
тока проводимости непрерывна на любой
поверхности раздела сред.
Последнее соотношение не учитывает наличие внешних источников тока. В более общем случае оно имеет вид
![]()
где G – ток внешнего источника, проходящий через единицу площади поверхности раздела сред.
