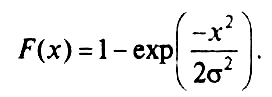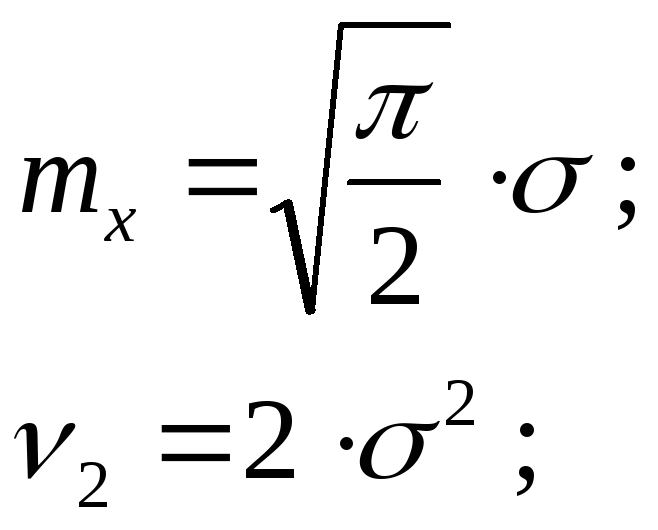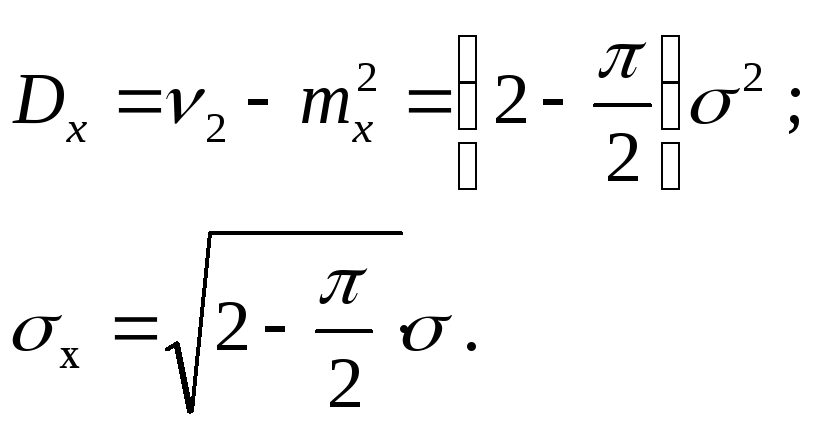5.1 Распределение Релея

Всвоей стандартной записиплотность вероятности распределения Релея определяется формулой

(5.4)

Интегральная функция распределения Рэлея определяется форму­лой:

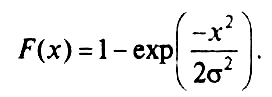
(5.5)

Графики плотности вероятности и функции распределения случай­ной величины, имеющей закон распределения Рэлея при = 1; ; 2, приведены на рис. 5.2.

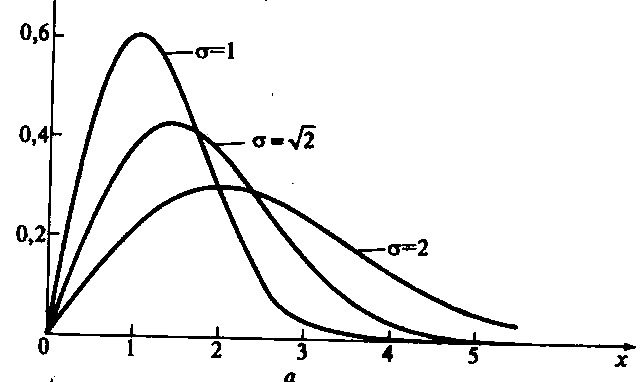
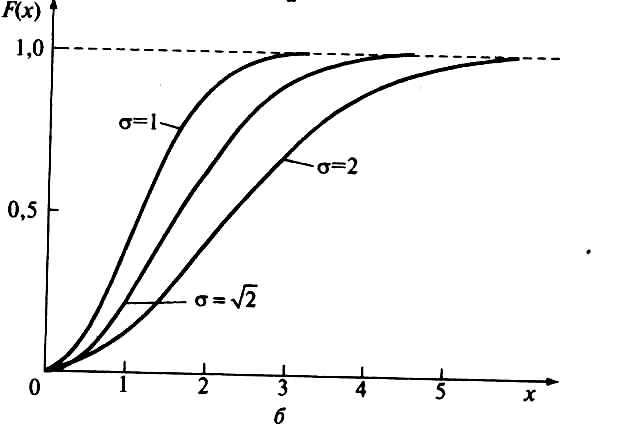
Рис.5.2 Плотность вероятности а) и функция распределения б) Релея.

Графики приведенные на Рис.5.2 показывают, что с увеличением значения параметра распределения увеличивается математическое ожидание 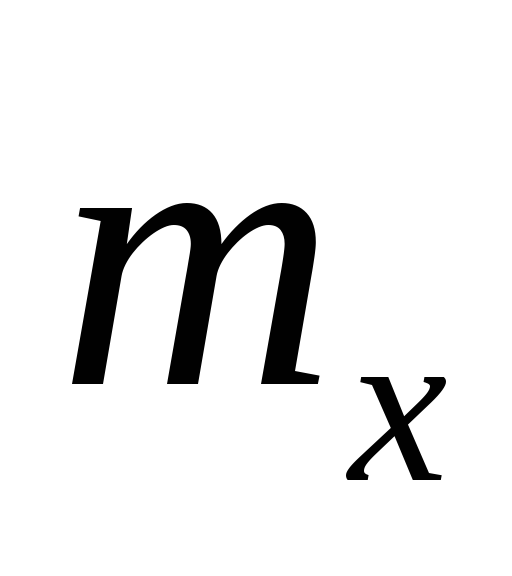и среднеквадратическое отклонениеслучайной величины.

Вычисления математического ожидания, на­чального момента второго порядка и дисперсии случайной величины, распределенной по закону Рэлея, дают следующие результаты:

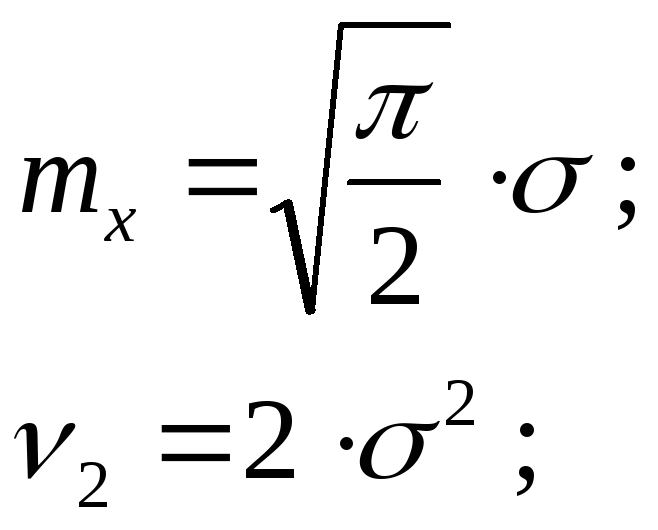
(5.6)

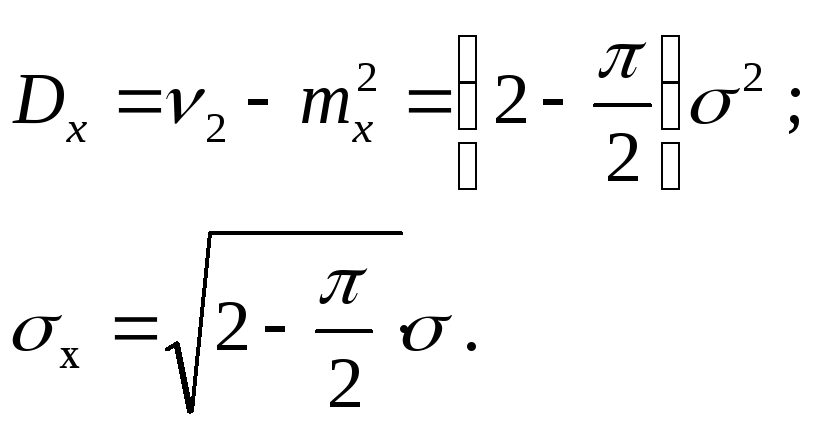
(5.7)

Автор: к.т.н.,доцент В.Е.Куприянов

08.09.2012г