
- •2007 Г.
- •Оглавление
- •Состав теоретического материала и ссылки на литературу
- •Справочный материал к выполнению контрольной работы
- •Функции нескольких переменных и ее частные производные
- •1.1. Определение функции нескольких переменных.
- •1.2. Частные производные фнп.
- •1.3. Полное приращение и полный дифференциал фнп.
- •1.4. Производные фнп высших порядков.
- •2. Частные производные фнп, заданной неявно
- •3. Производная сложной фнп. Полная производная
- •4. Экстремумы фнп
- •4.1. Локальные максимумы и минимумы фнп.
- •4.2 Нахождение наибольшего и наименьшего значений фнп в замкнутой области
- •5. Касательная плоскость и нормаль к поверхности
- •6. Скалярное поле. Градиент. Производная по направлению
- •7. Функции комплексной переменной
- •7.1. Определение и свойства функции комплексной переменной.
- •7.2. Дифференцирование фкп. Аналитические фкп.
- •Решение примерного варианта контрольной работы
- •Рекомендуемая литература
6. Скалярное поле. Градиент. Производная по направлению
Говорят,
что в области ![]() задано скалярное
поле,
если в каждой точке M(x, y) D
задана скалярная функция координат
точки:
задано скалярное
поле,
если в каждой точке M(x, y) D
задана скалярная функция координат
точки:
U(M) = U(x, y).
Пример:скалярное поле температурT(x, y)в областиD.
Линии уровня скалярного поля– это такие линии, на каждой из которых функцияU(x,y)сохраняет постоянное значение.
Уравнения линий уровня скалярного поля:U(x, y) = const.
Геометрически линии уровня получаются, если поверхность z= U(x, y) пересекать горизонтальными плоскостями z=С и проектировать линии пересечения на плоскость XOY.
Градиентом
скалярного поля U(x, y)
в фиксированной точке
![]() называется вектор, проекции которого
на оси координат совпадают с частными
производными функции, вычисленными в
точке М0:
называется вектор, проекции которого
на оси координат совпадают с частными
производными функции, вычисленными в
точке М0:
![]() , (7)
, (7)
где
векторы
![]() – это орты координатных осей.
– это орты координатных осей.
Вектор
градиента
![]() направлен перпендикулярно касательной
к линии уровня, проходящей через точкуМ0.
Направление градиента указывает
направление наибольшего роста функции
U(x, y)
в
точке М0
.
направлен перпендикулярно касательной
к линии уровня, проходящей через точкуМ0.
Направление градиента указывает
направление наибольшего роста функции
U(x, y)
в
точке М0
.
Отложим от
фиксированной точки M0(x0, y0)
некоторый вектор
![]() .
.
Скорость
изменения скалярного
поля
U(x, y)
в
точке М0
в направлении вектора
![]() характеризует величина
характеризует величина![]() ,
называемаяпроизводной
по направлению.
,
называемаяпроизводной
по направлению.
Если в прямоугольной
системе координат XОY
вектор
![]() имеет направляющие косинусы cos
и cos,
то производная по направлению вектора
имеет направляющие косинусы cos
и cos,
то производная по направлению вектора
![]() в точкеМ0
– число
в точкеМ0
– число
![]() – можно найти по формуле:
– можно найти по формуле:
![]() ,
(8)
,
(8)
Напомним
формулы для вычисления направляющих
косинусов вектора
![]() :
:![]() ,
где модуль вектора:
,
где модуль вектора:![]() .
.
Аналогично определяют скалярное поле U(M) в трехмерной области V:
U(M)
=
U(x, y, z)
![]() .
Поверхности
уровня скалярного
поля– это такие
поверхности, на каждой из которых функцияU(x, y, z)сохраняет постоянное значение.Уравнения
поверхностей уровня скалярного поля:U(x, y, z)
= const.
.
Поверхности
уровня скалярного
поля– это такие
поверхности, на каждой из которых функцияU(x, y, z)сохраняет постоянное значение.Уравнения
поверхностей уровня скалярного поля:U(x, y, z)
= const.
Градиент скалярного поля U(x, y, z) в произвольной точке M(x, y, z):
![]() , (9)
, (9)
где
векторы
![]() – это орты координатных осей.
– это орты координатных осей.
Вектор
![]() направлен параллельно нормали к
поверхности уровняU(x, y, z)
= const в точке
М.
направлен параллельно нормали к
поверхности уровняU(x, y, z)
= const в точке
М.
7. Функции комплексной переменной
7.1. Определение и свойства функции комплексной переменной.
Пусть
даны две плоскости комплексных чисел
и на первой – множество D
комплексных чисел
![]() ,
гдеi
– мнимая
единица (
,
гдеi
– мнимая
единица (![]() ),
на второй – множествоG
комплексных
чисел
),
на второй – множествоG
комплексных
чисел
![]() .
.
Если
каждому числу
![]() по некоторому правилуf
поставлено в соответствие определенное
число
по некоторому правилуf
поставлено в соответствие определенное
число
![]() ,
то говорят, что на множествеD
задана однозначная функция
комплексной переменной
(ФКП),
отображающая
множество D
в множество G.
Обозначается:
,
то говорят, что на множествеD
задана однозначная функция
комплексной переменной
(ФКП),
отображающая
множество D
в множество G.
Обозначается:
![]() .
.
Множество D называется областью определения ФКП.
Функцию
![]() можно представить в виде
можно представить в виде
![]() ,
,
где u(x, y) – действительная часть ФКП, v(x, y) – мнимая часть ФКП, обе они – действительные функции от x, y.
Пример
1.
![]() .
Здесь
.
Здесь![]() – число, сопряженное числу
– число, сопряженное числу![]() .
.
Выделим действительную и мнимую части ФКП:
![]() Вычислим
значение функции w
в точке z1
= 2 – 3i:
Вычислим
значение функции w
в точке z1
= 2 – 3i:
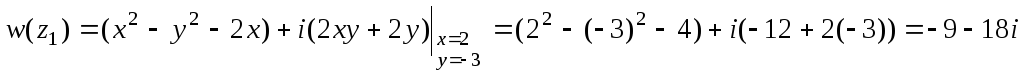 .
.
Тот же результат получаем непосредственной подстановкой:
![]() .
.
Говорят,
что ФКП
![]() имеет предел
в точке z0,
равный числу A
= a
+ ib,
если
имеет предел
в точке z0,
равный числу A
= a
+ ib,
если
![]() .
Обозначается:
.
Обозначается:![]() .
.
Существование
предела ФКП
![]() при
при![]() в означает существование двух пределов:
в означает существование двух пределов: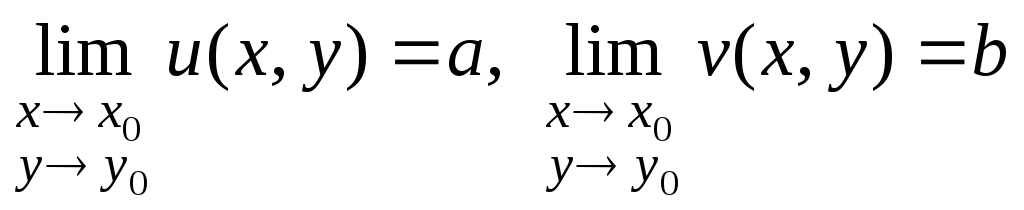 .
.
ФКП
![]() называетсянепрерывной
в точке z0,
если выполняется условие:
называетсянепрерывной
в точке z0,
если выполняется условие:
![]() .
.
Непрерывность
ФКП
![]() в точкеz0
= x0
+ iy0
эквивалентна непрерывности функций
u(x, y)
и v(x, y)
в точке (x0,y0).
в точкеz0
= x0
+ iy0
эквивалентна непрерывности функций
u(x, y)
и v(x, y)
в точке (x0,y0).
