
- •2007 Г.
- •Оглавление
- •Состав теоретического материала и ссылки на литературу
- •Справочный материал к выполнению контрольной работы
- •Функции нескольких переменных и ее частные производные
- •1.1. Определение функции нескольких переменных.
- •1.2. Частные производные фнп.
- •1.3. Полное приращение и полный дифференциал фнп.
- •1.4. Производные фнп высших порядков.
- •2. Частные производные фнп, заданной неявно
- •3. Производная сложной фнп. Полная производная
- •4. Экстремумы фнп
- •4.1. Локальные максимумы и минимумы фнп.
- •4.2 Нахождение наибольшего и наименьшего значений фнп в замкнутой области
- •5. Касательная плоскость и нормаль к поверхности
- •6. Скалярное поле. Градиент. Производная по направлению
- •7. Функции комплексной переменной
- •7.1. Определение и свойства функции комплексной переменной.
- •7.2. Дифференцирование фкп. Аналитические фкп.
- •Решение примерного варианта контрольной работы
- •Рекомендуемая литература
1.3. Полное приращение и полный дифференциал фнп.
Полным
приращением функции двух переменных![]() в точке (х,у), вызванным приращениями
аргументов
в точке (х,у), вызванным приращениями
аргументов![]() и
и![]() ,
называется выражение
,
называется выражение
![]() .
.
Функция
![]() называетсянепрерывной в точке(х,у), если бесконечно малым
приращениям аргументов соответствует
бесконечно малое приращение функции.
называетсянепрерывной в точке(х,у), если бесконечно малым
приращениям аргументов соответствует
бесконечно малое приращение функции.
Если обозначить![]() – расстояние между близкими точками
– расстояние между близкими точками![]() и (х, у), то
и (х, у), то![]() – этоопределение
непрерывности ФНП на языке приращений.
– этоопределение
непрерывности ФНП на языке приращений.
Если функция![]() непрерывна в любой точке (х, у)D,
то она называетсянепрерывной
ФНП в области D.
непрерывна в любой точке (х, у)D,
то она называетсянепрерывной
ФНП в области D.
Функция![]() ,
полное приращениеzкоторой в данной точке(x, y)может быть представлено в виде суммы
двух слагаемых: выражения, линейного
относительно
,
полное приращениеzкоторой в данной точке(x, y)может быть представлено в виде суммы
двух слагаемых: выражения, линейного
относительно![]() и
и![]() ,
и величины, бесконечно малой более
высокого порядка малости относительно
,
и величины, бесконечно малой более
высокого порядка малости относительно![]() ,
называетсядифференцируемой
функцией в данной точке,
а линейная часть ее полного приращения
называетсяполным
дифференциалом ФНП.
,
называетсядифференцируемой
функцией в данной точке,
а линейная часть ее полного приращения
называетсяполным
дифференциалом ФНП.
Если
![]() ,
где
,
где![]() –бесконечно малые при
–бесконечно малые при![]() ,
то полный дифференциал функции
,
то полный дифференциал функции![]() выражается
формулой:
выражается
формулой:
![]() ,
или:
,
или:
![]() (1)
(1)
(приращения независимых переменных совпадают с их дифференциалами: х=dx,y=dy).
Из определения полного
дифференциала следует его связь с полным
приращением: при
малых![]() и
и![]()
![]() с точностью до бесконечно
малых более высокого порядка малости
относительно
с точностью до бесконечно
малых более высокого порядка малости
относительно![]() .
.
Полный дифференциал функции
![]() зависит как от точкиM(x0,y0),
в которой он вычисляется, так и от
приращений
зависит как от точкиM(x0,y0),
в которой он вычисляется, так и от
приращений![]() и
и![]() .
.
1.4. Производные фнп высших порядков.
Пусть функция z = f (x, y)
имеет в точке (x, y)
и её окрестности имеет непрерывные
частные производные первого порядка![]() и
и![]() .
Так как
.
Так как![]() и
и![]() являются функциями тех же аргументовx и y, то их можно дифференцировать
поxи поy. При этом возможны
следующие 4 варианта:
являются функциями тех же аргументовx и y, то их можно дифференцировать
поxи поy. При этом возможны
следующие 4 варианта:
![]()
![]()
– эти частные производные называютсячастными
производными второго порядкаот функции![]() .
.
Частные
производные
![]() и
и![]() называютсясмешанными
частными производными второго порядка.
называютсясмешанными
частными производными второго порядка.
Пример.Дана ФНП![]() .
Вычислим все её частные производные
второго порядка.
.
Вычислим все её частные производные
второго порядка.
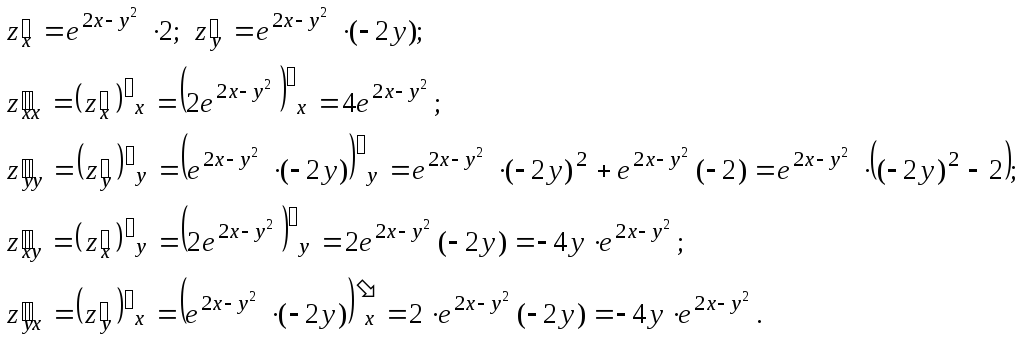
Основное свойство смешанных частных
производных: если функцияz = f (x, y)и её частные производные![]() ,
,![]() ,
,![]() и
и![]() определены и непрерывны в точке(x, y)и некоторой её окрестности, то в этой
точке
определены и непрерывны в точке(x, y)и некоторой её окрестности, то в этой
точке![]() =
=![]() ,
то есть смешанные частные производные
при условии их непрерывности не зависят
от порядка, в котором производится
дифференцирование.
,
то есть смешанные частные производные
при условии их непрерывности не зависят
от порядка, в котором производится
дифференцирование.
2. Частные производные фнп, заданной неявно
Если каждой паре чисел(x, y)из некоторой области![]() соответствует
одно или несколько значенийz,
удовлетворяющих уравнению
соответствует
одно или несколько значенийz,
удовлетворяющих уравнению![]() ,
то это уравнение неявно определяет
функцию 2-х переменных
,
то это уравнение неявно определяет
функцию 2-х переменных![]() .
.
Если существуют частные производные
функции F(x, y, z):![]() и
и![]() ,
то существуют частные производные от
функцииz (x, y),
которые можно вычислить по формулам:
,
то существуют частные производные от
функцииz (x, y),
которые можно вычислить по формулам:
![]() .(2)
.(2)
Пример.Дано:![]() .
Найти
.
Найти![]() и
и![]() .
.
Здесь
![]() .
По формулам (2) находим:
.
По формулам (2) находим:
![]()
Уравнение
![]() неявно определяет еще две функции 2-х
переменных:
неявно определяет еще две функции 2-х
переменных:![]() и
и![]() .
Частные производные этих функций можно
найти по формулам, аналогичным формуле
(2), например:
.
Частные производные этих функций можно
найти по формулам, аналогичным формуле
(2), например:
![]() . (3)
. (3)
3. Производная сложной фнп. Полная производная
Пусть функция z= f (x, y, t)
– функция трех переменныхx,y иt, причемxиy,
в свою очередь, являются функциями
независимой переменнойt,
тогда![]() – это сложная функция одной переменнойt, аxиy –
промежуточные переменные.
– это сложная функция одной переменнойt, аxиy –
промежуточные переменные.
Полной
производной по переменной t сложной ФНП![]() называется её производная
называется её производная![]() ,
вычисленная как производная функции
одной переменнойtв предположении, что переменныеxиy
также являются функциями
от
t, то есть приx=x(t)
иy = y(t):
,
вычисленная как производная функции
одной переменнойtв предположении, что переменныеxиy
также являются функциями
от
t, то есть приx=x(t)
иy = y(t):
![]() . (4)
. (4)
Здесь
![]() – это полная производная функцииzпо переменнойtпри условии, что все
другие переменные зависят отt,
а
– это полная производная функцииzпо переменнойtпри условии, что все
другие переменные зависят отt,
а![]() – это частная производная функцииzпо переменнойtпри условии, что у
функции есть другие независимые
переменные, кромеt.
При ее нахождении зависимость переменныхx,y
от t не
учитывается.
– это частная производная функцииzпо переменнойtпри условии, что у
функции есть другие независимые
переменные, кромеt.
При ее нахождении зависимость переменныхx,y
от t не
учитывается.
В полученный ответ следует подставить функции x = x(t) и y = y(t), чтобы выразить полную производную через независимую переменную t.
