5.2. Формула Остроградского-Гаусса. Дивергенция

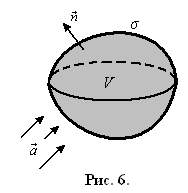
Формула Остроградского-Гаусса устанавливает связь между интегралом по замкнутой поверхности σ в направлении ее «внешней» нормали и тройным интегралом по областиV, ограниченной этой поверхностью:

.

Пусть – векторное поле, заданное в областиVxOyz.Дивергенцией векторного поля называется скалярная функция

, (7)

которая характеризует наличие источников (если div> 0) и стоков (если div< 0), или их отсутствие (если div= 0) векторного поля в точке М.

Используя выражения для дивергенции и для потока вектора через замкнутую поверхность σ, можно записать формулу Остроградского-Гаусса в векторном виде:

, (8)

т.е. поток вектора через замкнутую поверхность σ в направлении ее «внешней» нормали (рис. 6) равен тройному интегралу от дивергенции этогополя по областиV, ограниченной поверхностьюσ.

6. Потенциальные и соленоидальные векторные поля

6.1. Ротор векторного поля

Ротором (вихрем) векторного поляназывается вектор

.

Ротор – это векторная величина, которая является дифференциальной характеристикой векторного поля. Всякое векторное поле сопровождается другим векторным полемего роторов.

Для вычисления ротора удобно использовать его запись в форме определителя:

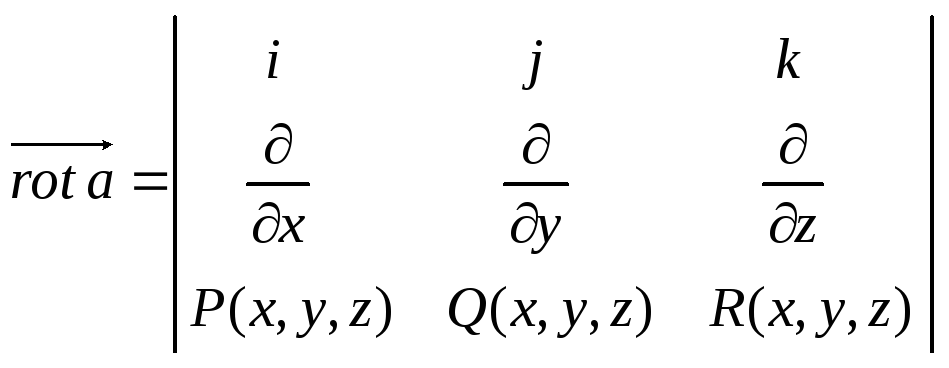,(9)

где вектор – это векторно-дифференциальный оператор, называемыйоператором Гамильтона или оператором«набла». При вычислении определителя умножению его элементовна функцииP,Q,Rсоответствует операция дифференцирования:,и т.д.

6.2. Потенциальное векторное поле и его потенциал

Векторное поле называетсяпотенциальным, если существует такая скалярная функцияU(x, y, z), что. ФункцияUназываетсяпотенциаломвекторного поля .

Из определения следует, что потенциальное векторное поле – это поле градиентов некоторого скалярного поля U(M) =U(x, y, z).

Пусть векторное поле задано в некоторой области V.

Область V называется односвязной, если любой замкнутый контур (кривую), лежащий в ней, можно путем непрерывной деформации стянуть в точку, не выходя за пределы данной области. Для плоской области D односвязность означает, что для любого замкнутого контура, лежащего в ней, ограниченная этим контуром часть области целиком принадлежит D.

Потенциальность векторного поля, заданного в односвязной области V, определяется при помощи его ротора: если во всех точках областиVротор векторного поля – нулевой вектор, то это векторное поле является потенциальным.

Важное свойство потенциальных полей заключается в том, что если – потенциальное векторное поле, заданное в некоторой односвязной областиV, то выражение

является полным дифференциалом функцииU(x, y, z). В этом случае криволинейный интеграл вида

вдоль любой кривой ВС, принадлежащейV, не зависит от формы кривой и равен разности потенциалов в конечной и начальной точках:

.

Это свойство можно использовать для нахождения потенциала векторного поля при помощи криволинейного интеграла IIрода. Для этого нужно взять фиксированную точкуВ(x₀, y₀, z₀) и произвольную (текущую) точкуС(x, y, z) и вычислить криволинейный интеграл по путиВС:

.

При этом получаем потенциалU(x, y, z) векторного поля с точностью до произвольного постоянного слагаемого.

В качестве пути интегрирования ВСобычно выбирают ломануюВEKC (рис. 7), звенья которой параллельны осям координат иE(x, y₀, z₀),K(x, y, z₀). В этом случае потенциалU(x, y, z) находят по формуле:

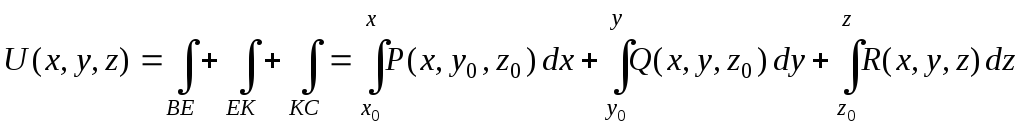. (10)

Если в односвязной области задано потенциальное векторное поле силы , то с помощью потенциала можно найти работу силы при перемещении единичной массы из одной заданной точкиM этой области в другую точку N как разность значений потенциалов в этих точках:

. (11)