
- •Оглавление
- •Введение
- •Задания на контрольную работу по теме «Интегральное исчисление функции нескольких переменных. Векторный анализ. Элементы теории векторного поля»
- •Содержание теоретического материала и ссылки на литературу
- •Справочный материал к выполнению контрольной работы
- •1. Двойной интеграл
- •1.1. Вычисление двойного интеграла в декартовых координатах
- •1.2. Вычисление двойного интеграла в полярных координатах
- •1.3. Некоторые приложения двойных интегралов
- •2. Тройной интеграл
- •2.1. Вычисление тройного интеграла в декартовых координатах
- •2.2. Вычисление тройного интеграла в цилиндрических координатах
- •2.3. Некоторые приложения тройных интегралов
- •3. Криволинейный интеграл II рода (по координатам)
- •4. Векторная функция скалярного аргумента
- •5. Векторное поле
- •5.1. Поток векторного поля через поверхность
- •5.2. Формула Остроградского-Гаусса. Дивергенция
- •6. Потенциальные и соленоидальные векторные поля
- •6.1. Ротор векторного поля
- •6.2. Потенциальное векторное поле и его потенциал
- •6.3. Соленоидальное векторное поле
- •Решение примерного варианта контрольной работы
- •Рекомендуемая литература
3. Криволинейный интеграл II рода (по координатам)
Общий вид криволинейного интеграла II рода(по координатам):
 ,
,
где BC – это дуга пространственной линии от точки B до точки C с указанным на ней направлением, P (x, y, z), Q (x, y, z), R (x, y, z) – некоторые функции, заданные во всех точках дуги BC.
В двумерном случае:
 ,
гдеBC
,
гдеBC![]() xOy.
xOy.
Если
P (x, y),
Q (x, y)
– проекции на оси Ox
и Oy
вектора переменной силы
![]() ,
то
,
то
![]() (3)
(3)
– это
работа силы
![]() при перемещении
точки ее приложения вдоль участка дуги
BC.
при перемещении
точки ее приложения вдоль участка дуги
BC.
Пусть
кривая BC
задана параметрически:
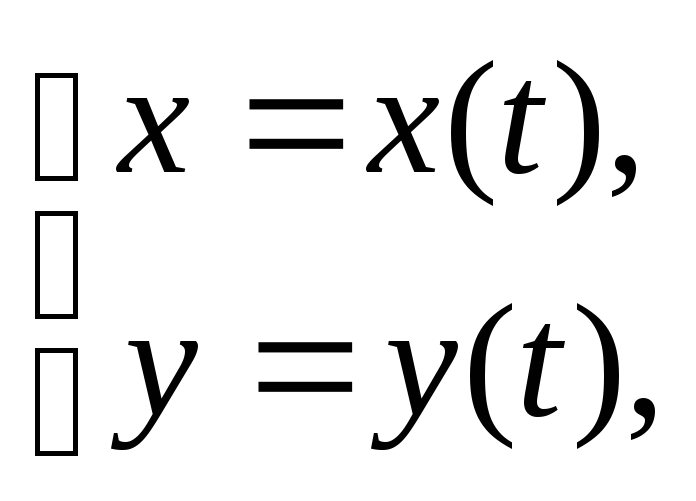 причем функцииx (t)
и y (t)
– непрерывны и дифференцируемы по t,
а tB,
tC
– значения параметра для начала и конца
кривой (в точках B
и C).
Тогда
причем функцииx (t)
и y (t)
– непрерывны и дифференцируемы по t,
а tB,
tC
– значения параметра для начала и конца
кривой (в точках B
и C).
Тогда
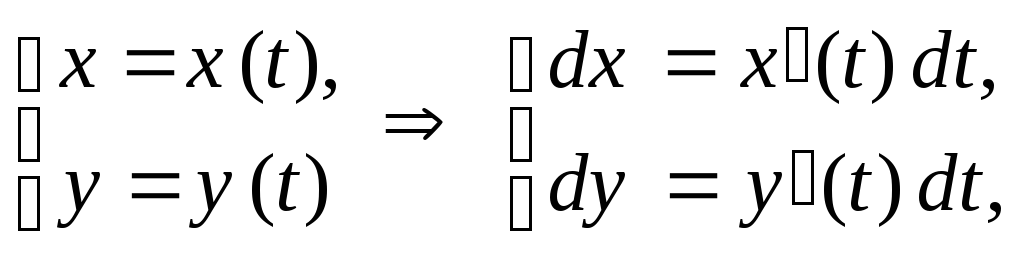
и вычисление криволинейного интеграла сводится к вычислению определенного интеграла по переменной t:
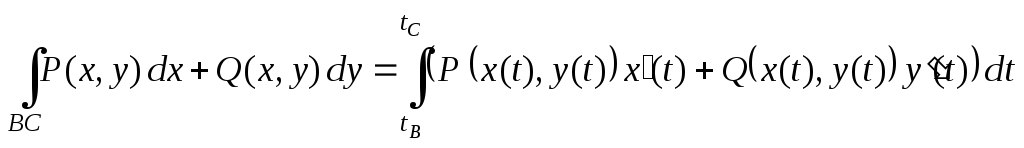 .
.
4. Векторная функция скалярного аргумента
Если каждому значению параметра tиз некоторого промежутка![]() ставится в соответствие по некоторому
правилу определенный вектор, то говорят,
что заданавектор-функция скалярного
аргументаt:
ставится в соответствие по некоторому
правилу определенный вектор, то говорят,
что заданавектор-функция скалярного
аргументаt:![]() .
.
Откладывая векторы
![]() при
при![]() от начала координат, получаем траекторию
движения конца вектора, называемуюгодографом вектор-функции
от начала координат, получаем траекторию
движения конца вектора, называемуюгодографом вектор-функции ![]() .
.
Проекции вектора
![]() на оси координат являются функциями
аргументаt, поэтому
можно записать вектор-функцию в
координатной форме:
на оси координат являются функциями
аргументаt, поэтому
можно записать вектор-функцию в
координатной форме:
![]() ,
,
где
векторы
![]() – это орты координатных осейOx,
Oy
и Oz.
– это орты координатных осейOx,
Oy
и Oz.
Первую, вторую и т.д. производные
вектор-функции
![]() находят дифференцированием ее проекцийx(t),y(t)
иz(t)
по аргументуt:
находят дифференцированием ее проекцийx(t),y(t)
иz(t)
по аргументуt:
![]() ,
,
![]() .
.
Если параметр t– это
время, то векторное уравнение![]() называютуравнением движенияточки,
а годограф вектор-функции
называютуравнением движенияточки,
а годограф вектор-функции![]() является траекторией движения. Тогда
вектор-производная называетсяскоростью
движения точки в момент времени t:
является траекторией движения. Тогда
вектор-производная называетсяскоростью
движения точки в момент времени t:
![]() .
(4)
.
(4)
Скорость движения – это вектор, направленный по касательной к траектории движения (годографу) в соответствующей точке в сторону возрастания параметра t.
Вектор
![]() (5)
(5)
называется ускорением движения точки в момент времени t.
5. Векторное поле
5.1. Поток векторного поля через поверхность
Если в любой точке M(x, y, z)
областиV![]() xOyzзадан вектор
xOyzзадан вектор![]() ,
то говорят, что в областиVзадановекторное поле
,
то говорят, что в областиVзадановекторное поле
![]() .
.
Примеры:
силовое поле![]() ,
поле скоростей
,
поле скоростей![]() текущей жидкости, поле электростатических
напряженностей
текущей жидкости, поле электростатических
напряженностей![]() .
.
Векторное поле является заданным, если
задана векторная функция
![]() от координат точкиM(x, y, z).
Как правило, функцию
от координат точкиM(x, y, z).
Как правило, функцию
![]() задают в координатной форме:
задают в координатной форме:![]() ,
,
где P (x, y, z),Q (x, y, z),R (x, y, z) являются функциями, о которых предполагают, что они непрерывны и имеют непрерывные частные производные поx, y, zв областиV (областьV может совпадать со всем пространством).
Аналогично
определяют плоское векторное поле ![]() в двумерной области D:
в двумерной области D:
![]() .
.
Пусть в области V![]() xOyzзадана двусторонняя поверхностьσ,
в каждой точке которой определенорт
внешней нормали
xOyzзадана двусторонняя поверхностьσ,
в каждой точке которой определенорт
внешней нормали![]() – единичной вектор, коллинеарный нормали
к поверхности в этой точке и направленный
в сторону, которую условились считать
«внешней» стороной поверхности.
– единичной вектор, коллинеарный нормали
к поверхности в этой точке и направленный
в сторону, которую условились считать
«внешней» стороной поверхности.
Поток
векторного
поля
![]() через поверхность σ
– это интеграл по поверхности σ
от скалярного
произведения вектора
через поверхность σ
– это интеграл по поверхности σ
от скалярного
произведения вектора
![]() на орт нормали
на орт нормали![]() к поверхности (рис. 5):
к поверхности (рис. 5):
![]() .
.
П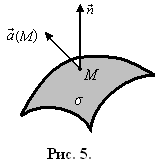 оток
– это интегральная характеристика
векторного поля, она является скалярной
величиной. Например, для поля скоростей
оток
– это интегральная характеристика
векторного поля, она является скалярной
величиной. Например, для поля скоростей![]() текущей жидкости поток характеризует
количество жидкости, проходящей через
поверхность
σ в направлении
«внешней» нормали в единицу времени.
текущей жидкости поток характеризует
количество жидкости, проходящей через
поверхность
σ в направлении
«внешней» нормали в единицу времени.
Е сли
поверхностьσзадана уравнениемF(x,y,z)
= 0, то вектор ее нормали коллинеарен
градиенту функции, задающей поверхность:
сли
поверхностьσзадана уравнениемF(x,y,z)
= 0, то вектор ее нормали коллинеарен
градиенту функции, задающей поверхность:![]() ,
следовательно, орт нормали
,
следовательно, орт нормали![]()
![]()
![]()
![]() .
.
Для
вычисления поверхностного интеграла
![]() поверхностьσ
проектируют на одну из координатных
плоскостей, например, в область D
поверхностьσ
проектируют на одну из координатных
плоскостей, например, в область D![]() xOy.
Тогда
xOy.
Тогда
![]()
![]() ,
и вычисление потока сводится к вычислению
двойного интеграла:
,
и вычисление потока сводится к вычислению
двойного интеграла:
![]() , (6)
, (6)
где
знак «+» следует брать в случае, когда
вектор
![]() и орт «внешней» нормали
и орт «внешней» нормали![]() ,
указанный в задаче, совпадают по
направлению; если эти векторы противоположны
по направлению, следует брать знак «–».
,
указанный в задаче, совпадают по
направлению; если эти векторы противоположны
по направлению, следует брать знак «–».
При
вычислении двойного интеграла ![]() нужно подынтегральную функцию выразить
через переменные x, y,
используя
заданное уравнение поверхности F(x,
y,
z)
= 0.
нужно подынтегральную функцию выразить
через переменные x, y,
используя
заданное уравнение поверхности F(x,
y,
z)
= 0.
Поток
вектора
![]() через
замкнутую поверхность
σ в
направлении
ее «внешней» нормали обозначают
через
замкнутую поверхность
σ в
направлении
ее «внешней» нормали обозначают ![]() .
.
