Popov / Popov / гидравлика / лаба№3

ПОСТРОЕНИЕ ПЬЕЗОМЕТРИЧЕСКОЙ И НАПОРНОЙ ЛИНИИ

Цель работы:

• Построить пьезометрическую и напорную линии для трубопровода круглого сечения;

• Определить значения пьезометрического и гидродинамического уклонов;

• Проследить, на каких участках происходит переход энергии из кинетической в потенциальную и обратно в соответствии с уравнением Бернулли.

1. Основные понятия

В гидродинамике уравнение Бернулли является аналогом известного закона сохранения энергии для двух контрольных сечений в канале 1—1 и 2—2 для течения идеальной жидкости имеет вид:

=const (1)

В случае течения реальной жидкости, имеет место сопротивление движению, приводящие к потерям энергии потока (потери напора) и (1) приобретает вид:

+h (2)

Где потери h равны разности энергий в двух контрольных сечениях потока. При этом конечно, всегда h>0, т. к. энергия вдоль потока только теряется.

z — удельная потенциальная энергия положения (или геометрический напор), измеряемая как разность высот от центра потока до плоскости отсчёта (нивелирной плоскости), выбираемой произвольно;

— удельная потенциальная энергия давления (или пьезометрический напор),

представляющая по своему смыслу величину давления, которое движущийся поток оказывает на стенки каналов;

—--удельная кинетическая энергия (или скоростной напор);

Таким образом, полная энергия потока (или гидродинамический напор)

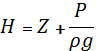+ — есть сумма потенциальной и кинетической энергии.

H=E_пот+E_кин

Если для канала, состоящего из нескольких участков одинакового диаметра,или равного диаметра построить зависимость изменения полной энергии потока Н вдоль канала Н =f(l), то графическая такая зависимость в координатах Н -l представляется наклонной ломаной линией и называется напорной линией. На каждом участке этой линии разность значений энергии H₁ в начале участка и H₂ в конце участка ΔН = Н₁—Н₂ — есть величина потери энергии на этом участке.

Аналогичным образом можно проследить за изменением не полной энергии потока, а лишь её потенциальной части и на каждом участке канала откладывать значения

Е_пот1= в начале участка и Е_пот2=в конце участка

Тогда разность Δ Е_пот = Е_пот1 - Е_пот2 показывает потери потенциальной энергии на этом участке. Графическая зависимость Е_пот = f(l) в координатах Н — l для всего канала называется пьезометрической линией.

Для характеристики гидродинамических качеств каналов вводится величина, называемая гидродинамическим уклоном и, представляющая собой по смыслу, потери полного напора на единицу длины канала.

На графической зависимости Н = f(l) гидродинамический уклон представляется тангенсом угла наклона напорной линии.

Аналогичным образом можно ввести величину

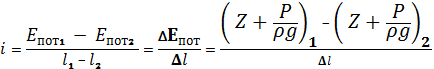
называемую пьезометрическим уклоном, и характеризующую потери потенциальной энергии на единицу длины канала. Также как и в гидродинамический уклон, пьезометрический уклон на графической зависимости Н = f(l) представляется тангенсом угла наклона пьезометрической линии.

В отличие от гидродинамического уклона, который всегда отрицателен (α <90°), поскольку полная энергия потока вдоль канала всегда только уменьшается, пьезометрический уклон может быть положительным (α >90°)- это будет иметь место там, где потенциальная энергия потока возрастает и пьезометрическая линия идет вверх.

Сближение напорной и пьезометрической линии означает, что кинетическая энергия переходит в потенциальную (диффузорное течение, т.е. течение в расширяющемся канале). Если же линии удаляются друг от друга, то это означает, что потенциальная энергия преобразуется в кинетическую – это имеет место при течении в сужающемся канале (конфузорное течение).

Из уравнения Д.Бернулли (1, 2) следует, что если площадь поперечного сечения струйки или потока уменьшается, то скорость течения жидкости увеличивается, а давление уменьшается, и, наоборот, если скорость при расширении уменьшается, то давление возрастает. Именно эта взаимосвязь между изменяющимися значениями скорости и давления (или между кинетической и потенциальной энергиями) находит самое широкое применение при решении ряда практических вопросов.

Таблица 1

№ п\п	Наименование величин	Расчетные значения	Сечение трубопровода
			1	2	3	4	5	6	7	8	9	10	11	12
1	Площадь сечения,м
2	Показания расходомера, V м3
3	Время замера, с
4	Расход жидкости, Q м/с
5	Средняя скорость м/с
6	Показания пьезометра
7	Скоростной напор
8	Полный напор,м

5. Выводы

В выводах следует проанализировать характер изменения пьезометрической линии и линии полной энергии полученной диаграммы на отдельных участках трубопровода и сопоставить опытные данные с теорией (уравнение Бернулли).

Так, например, на участках трубопровода, где происходит внезапное сужение потока, должно наблюдаться резкое понижение пьезометрического напора. Наоборот, на участках с внезапным расширением потока должно наблюдаться восстановление пьезометрического напора и т.п.

Рис.2 Пример построения пьезометрической и напорной линии

4