Лекция 20. Уравнения третьей степени. Формула

КОРДАНО.

Уравнение третьей степени с комплексными коэффициентами имеет вид:

(1)

Без ограничения общности можно считать, что старший коэффициент равен единице; в противном случае мы поделили бы обе части уравнения на старший коэффициент.

Подвергнем (1) упрощению – сделаем член с квадратом неизвестного равным нулю, для чего положим и найдем .

Таким образом, сделав в (1) подстановку , получим неполное кубическое уравнение:

(2)

Чтобы найти корни уравнения (2), положим , где u и v – два новых вспомогательных неизвестных. (2) запишем в виде:

,

раскрыв скобки и перегруппировав члены, получим:

.

Потребуем, чтобы или . Это требование всегда выполнимо, т.к. оно вместе с условием означает, что u и v являются корнями квадратного уравнения.

Тогда уравнение (2) приведется к уравнениям:

Отсюда согласно формулам Виета являются корнями квадратного уравнения:

откуда

.

Итак, неполное уравнение (2) решено в радикалах:

(3)

(3) – формула Кардана.

Формула Кардана состоит из суммы двух кубических радикалов. Каждый из них имеет три значения. Комбинируя значения u и v, получим девять сумм u+ v ,но среди них только три корня уравнения (2). Это будут те суммы u+ v, у которых u и v связаны соотношением:

(4)

Обозначим через , какую-нибудь пару значений , удовлетворяющих (4), а через - один из первообразных корней третьей степени из единицы. Например:.

Тогда , . Найдем . Так как и , то

, откуда

, откуда .

Таким образом, получим все значения корней неполного кубического уравнения (2):

, , .

Учитывая, что , , имеем: (5)

Пример. Определить по формуле Кардана корни уравнения:

, .

,

Обозначим - выражение стоящее под знаком квадратного радикала в формуле Кардана.

Предложение Если, то уравнение (2) имеет три различных корня.

Покажем, что , , , где - первообразный корень третьей степени из 1.

Пусть , , . Возведя обе части равенства в куб получим : , т.е. квадратное уравнение имеет два равных корня: , что невозможно, т.к. дискриминант этого квадратного уравнения . Тогда из формул (5) , т.к. при . Если бы , то , т.е.

, что при невозможно.

Аналогично обнаруживается, что .

Если прии , то

. Так как ,то . Следовательно .

Откуда одно из значений : . Соответствующее значение :

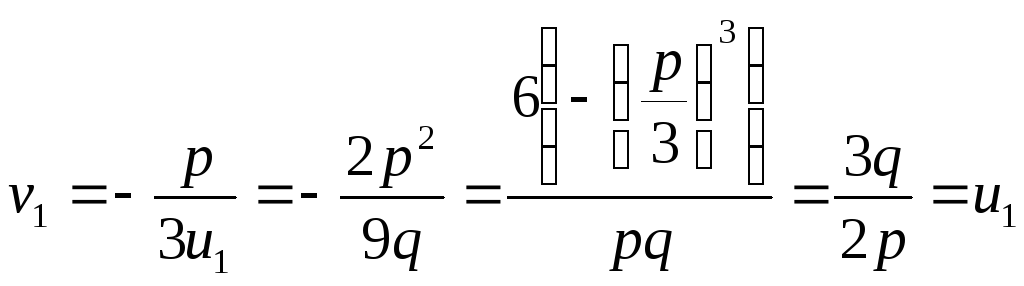
Обращаясь к формулам (5) получим:

Предложение: При (и ) уравнение (2) имеет два равных корня: , и в этом случае корни (2) можно найти, не прибегая к извлечению корней второй и третьей степеней, а именно: , (6)

Пример: Решить уравнение: .

УРАВНЕНИЯ ТРЕТЬЕЙ СТЕПЕНИ С ДЕЙСТВИТЕЛЬНЫМИ КОЭФФИЦИЕНТАМИ.

Пусть (7) – неполное кубическое уравнение третьей степени с действительными коэффициентами и .

Теорема: Если, то уравнение (7) имеет один действительный и два мнимых сопряженных корня;

если , то корни уравнения (7) действительны и хотя бы один из них кратный;

если, то то все корни (7) действительны и различны.

1. . Так как , то все три корня уравнения (7) должны быть различными.

Рассмотрим выражение .

Так как , то - действительное число. Следовательно, одно из значений и должно быть действительным. Пусть , тогда . На основании (5) уравнение (7) имеет только один действительный корень: , а два остальных корня будут сопряженными чисто комплексными числами:

,

.

2. . При , , уравнение имеет два равных корня. Так как (7) уравнение с действительными коэффициентами, то при , , все три корня уравнения действительны, причем два из них равны.

При , , уравнение (7) имеет три равных нулю корня: .

3. ( неприводимый случай). Так как , то , где . Тогда. Найдем модульи аргумент подкоренного выражения:

, . Т.о. .

Полагая получим:

.

Произведение комплексного числа на сопряженное равно квадрату модуля:

.

Найдем

, т.е. , но . Значит . Тогда

Тогда корни (7) имеют вид:

(8)

Итак, в случае уравнение (7) имеет три действительных корня.

Недостаток формулы Кардана состоит в том, что она часто представляет рациональные корни в иррациональном виде.

Пример. Очевидно - действительный корень.

( один действительный и два сопряженных мнимых корня)

По формуле Кардана: - иррациональные числа

При приближенных вычислениях , . Вследствие этого недостатка рациональные корни кубического уравнения с рациональными коэффициентами определяют не по формуле Кардана.

УРАВНЕНИЯ ЧЕТВЕРТОЙ СТЕПЕНИ.

Пусть (1) –

Уравнение четвертой степени с комплексными коэффициентами. Наиболее ранний способ решения (1) принадлежит Феррари ученику Кардана.

(2)

Подберем вспомогательное неизвестное так, чтобы правая часть (2) превратилась в полный квадрат. Что возможно при условии, что , где , , . Если , сравнивая коэффициенты при : , , , откуда . Обратно, если , то .

Подставляя в равенство выражения А, В,С, находим, что .

(3)

(3)- кубическая резольвента.

Пусть - какой-нибудь корень уравнения (3). Подставляя в (2) в правой части получим полный квадрат:

Откуда

Эти два квадратных уравнения дадут все четыре корня уравнения (1). Итак, решение уравнения четвертой степени сводится к решению одного уравнения третьей степени и двух уравнений второй степени, и так же решается в радикалах. При нахождении корней уравнения типа (1) по способу Феррари проводят последовательно все преобразования, не запоминая кубическую резольвенту.

Пример.

, ,

II способ Левая часть уравнения раскладывается на два множителя второй степени, которые последовательно приравниваются к нулю. Для нахождения такого разложения левую часть представляют как разность квадратов, для чего сначала представляют ее как разность между квадратом некоторого квадратного трехчлена и многочленом второй степени: - (члены степени не больше двух), оставляя пока неопределенным. В вычитаемое при этом входят лишние члены уменьшаемого( члены степени не больше 2) и такие же члены левой части (с обратным знаком). Для того, чтобы вычитаемое было полным квадратом, надо, чтобы его дискриминант был равен нулю. Это условие дает уравнение третьей степени относительно . Беря в качестве любой корень этого уравнения, получаем искомое.

Пример.

1)

, , ,

, ,

*2)