
- •Оглавление
- •Введение:
- •Глава l: Теоретическая часть
- •Метод прямоугольников.
- •Метод трапеций.
- •Метод Симпсона.
- •Процесс Эйткена.
- •Метод Монте-Карло.
- •Глава ll: Практическая часть (реализация в пакете Mathcad)
- •Реализация методов прямоугольников, трапеций, Симпсона.
- •Реализация метода Монте-Карло.
- •Заключение.
Процесс Эйткена.
У всех рассмотренных выше обобщенных формул на равномерных и квазиравномерных сетках ошибку можно разложить в ряд по степеням шага. К ним применим метод Рунге. Но для его применения надо знать, каков порядок точности исходной формулы.
Предположим, что порядок точности p существует, но неизвестен. Оказывается и в данном случае можно уточнить результат, если расчеты проведены на трех (или более) сетках.
Чтобы
упростить алгоритм расчета, выберем
три сетки с постоянным отношением шагов,
т.е. с шагами
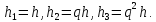 Обозначим приближенное значение
интеграла наK-й
сетке через
Обозначим приближенное значение
интеграла наK-й
сетке через
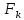 и ограничимся главным членом погрешности.
Тогда можно записать
и ограничимся главным членом погрешности.
Тогда можно записать
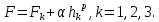 (12)
(12)
Это
система трех уравнений для определения
неизвестных F,
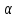 ,p.
Вводя вспомогательные обозначения
,p.
Вводя вспомогательные обозначения
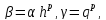 преобразуем эту систему к следующему
виду:
преобразуем эту систему к следующему
виду:
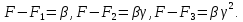 (13)
(13)
Перемножая крайние уравнения (13) и сравнивая с квадратом среднего уравнения, получим
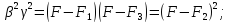 отсюда легко
получить уточненное значение интеграла
отсюда легко
получить уточненное значение интеграла
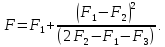 (14)
(14)
Попарно вычитая уравнения (13) друг из друга, получим
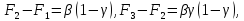
или
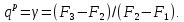
Следовательно, эффективный порядок точности исходной формулы (12) равен:
 .
(15)
.
(15)

Описанный
алгоритм был предложен Эйткеном в 1937г.
Для ускорения сходимости итерационных
процессов последовательного приближения,
в которых ошибка убывает примерно по
геометрической прогрессии. Погрешность
численного интегрирования при изменении
шага в q
раз меняется
приблизительно в
 раз. Поэтому если сетки последовательно
сгущаются в одно и то же число раз, то
ошибка убывает именно по требуемому
закону.
раз. Поэтому если сетки последовательно
сгущаются в одно и то же число раз, то
ошибка убывает именно по требуемому
закону.
Вычисляя
уточненное значение следует именно по
формуле (14), не преобразовывая её. В
данной записи из
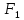 вычитается поправка, в которой числитель
и знаменатель имеют одинаковый порядок
малости, поэтому заметной потери точности
не происходит. Если же привести все
члены в формуле к общему знаменателю,
то в вычислениях придется удерживать
много знаков, чтобы избежать потери
точности при округлениях.
вычитается поправка, в которой числитель
и знаменатель имеют одинаковый порядок
малости, поэтому заметной потери точности
не происходит. Если же привести все
члены в формуле к общему знаменателю,
то в вычислениях придется удерживать
много знаков, чтобы избежать потери
точности при округлениях.
Метод Монте-Карло.
Во многих задачах исходные данные носят случайный характер, поэтому для их решения должен применяться статистико-вероятностный подход. На основе таких подходов построен ряд численных методов, которые учитывают случайный характер вычисляемых или измеряемых величин. К ним принадлежит и метод статистических испытаний, называемый также методом Монте-Карло, который применяется к решению некоторых задач вычислительной математики, в том числе и для вычисления интегралов.
Метод
Монте-Карло состоит в том, что
рассматривается некоторая случайная
величина
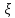 ,
математическое ожидание которой равно
искомой величине
,
математическое ожидание которой равно
искомой величине
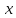 :
:
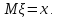
Проводится
серия
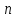 независимых испытаний, в результате
которых получается (генерируется)
последовательность
независимых испытаний, в результате
которых получается (генерируется)
последовательность
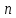 случайных чисел
случайных чисел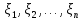 (выборка), имеющих то же распределение,
что и
(выборка), имеющих то же распределение,
что и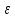 ,
и по совокупности этих значений находится
выборочное среднее
,
и по совокупности этих значений находится
выборочное среднее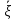 ,
которое является статистической оценкой
,
которое является статистической оценкой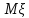 .
Искомая величина
.
Искомая величина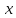 полагается приближенно равной этой
оценке
полагается приближенно равной этой
оценке
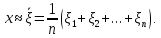
Пусть
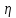 – равномерно распределена на отрезке
[0,1] случайная величина. Это означает,
что её плотность распределения задается
соотношением
– равномерно распределена на отрезке
[0,1] случайная величина. Это означает,
что её плотность распределения задается
соотношением
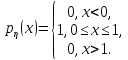
Тогда
любая функция
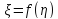 также будет случайной величиной, и её
математическое ожидание равно
также будет случайной величиной, и её
математическое ожидание равно
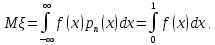
Следовательно,
читая это равенство и в обратном порядке,
приходим к выводу, что интеграл
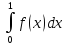 может быть вычислен как оценка
математического ожидания некоторой
случайной величины
может быть вычислен как оценка
математического ожидания некоторой
случайной величины
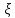 ,
которая является функцией случайной
величины
,
которая является функцией случайной
величины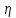 с равномерным законом распределения,
причем оценка
с равномерным законом распределения,
причем оценка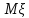 определяется независимыми реализациями
определяется независимыми реализациями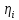 случайной величины
случайной величины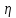 :
:
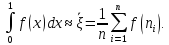
Аналогично могут быть и вычислены и кратные интегралы. Для двойного интеграла получим
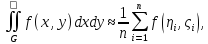
Где
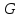 – квадрат
– квадрат
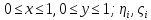 – независимые реализации случайных
величин
– независимые реализации случайных
величин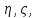 равномерно распределенных на отрезке
[0,1].
равномерно распределенных на отрезке
[0,1].
Для использования метода Монте-Карло при вычислении определенных интегралов, необходимо вырабатывать последовательности случайных чисел с заданным законом распределения. Существуют различные способы генерирования таких чисел.
Можно построить некоторый физический процесс (генератор) для выработки случайных величин, однако при использовании компьютера этот способ не применяется, поскольку, во-первых, трудно дважды получить одинаковые совокупности случайных чисел, которые необходимы при отладке программ, а во-вторых, такой физический генератор существенно усложнил бы конструкцию компьютера.
Известны многие таблицы случайных чисел, которые вычислялись независимо. Их можно ввести в компьютер и при необходимости обращаться к ним.
В настоящее время наиболее распространенный способ выработки случайных чисел на компьютере состоит в том, что в памяти хранится некоторый алгоритм получения таких чисел по мере потребности в них (подобно тому как вычисляются значения элементарных функций, а не хранятся их таблицы). Поскольку эти числа генерируются по наперед заданному алгоритму, то они не совсем случайны (псевдослучайны), хотя и обладают свойственными случайным числам статистическими характеристиками. В современных языках программирования такие алгоритмы реализованы в виде подпрограмм — датчиков случайных чисел.
