
- •Самостоятельная работа № 3 по химии
- •3. Разложение пентаоксида азота по реакции
- •Пример 4. Определение константы химического равновесия
- •Раздел 2. Приобретение компетенций и закрепление навыков
- •Б) Домашнее задание № 3 для закрепления знаний теоретического материала
- •По теме «Скорость химической реакции, её зависимость от
- •Природы реагентов, концентрации и температуры. Химическое
- •Равновесие. Условия смещения равновесия»
Самостоятельная работа № 3 по химии
Раздел 1. Обучающие примеры с алгоритмами решения по теме
«Скорость химической реакции, её зависимость от природы реагентов, концентрации и температуры. Химическое равновесие. Условия смещения равновесия»
Пример 1.Расчеты, основанные на применении закона действующих масс для
химических процессов, проходящих в гомогенной и гетерогенной среде
1. В результате реакции цинка сульфида с соляной кислотой за 6 мин образовалось 10,2 л сероводорода (н. у.). При взаимодействии цинка селенида в тех же условиях за такой же промежуток времени образовалось 4,48 л селеноводорода. Можно ли утверждать, что первая реакция протекает с большей скоростью?
Решение. Поскольку речь идет о химических процессах, запишем вначале уравнения реакций, о которых идет речь в задаче:
 ↑
и
↑
и ↑.
↑.
Уравнения реакций показывают, что объемы
выделяющихся газов в первой
 и второй
и второй реакциях эквивалентны количествам
веществ
реакциях эквивалентны количествам
веществ и
и ,
израсходованных в процессе. Это означает,
что
,
израсходованных в процессе. Это означает,
что и
и .
.
Поскольку количество вещества любого
газа при нормальных условиях прямо
пропорционально его объему, отнесенному
к молярному объему газа ( ),
то
),
то ;
;
и  .
.
Следовательно, и количество вещества
цинка сульфида за 6 мин уменьшилось на
0,45 моль
 ,
а количество вещества цинка селенида
уменьшилось только на 0,20 моль
,
а количество вещества цинка селенида
уменьшилось только на 0,20 моль .
.
Согласно уравнению средней скорости
химического процесса
 .
В этом уравнении объем реакционного
сосудаVпримем равным 1
л, а промежуток времени Δτ известен по
условию задачи, он равен 6 мин или
.
В этом уравнении объем реакционного
сосудаVпримем равным 1
л, а промежуток времени Δτ известен по
условию задачи, он равен 6 мин или .
Подставив значенияVи Δτ
в уравнение для скорости и произведя
расчеты, получим:
.
Подставив значенияVи Δτ
в уравнение для скорости и произведя
расчеты, получим:
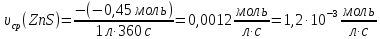 ;
;
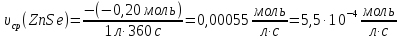 .
.
И тогд .
.
Как показывают расчеты, скорость реакции взаимодействия соляной кислоты с цинка сульфидом в 2 раза больше, чем скорость реакции с цинка селенидом.
Ответ: да, можно утверждать, что
первая реакция протекает с большей
скоростью, т.к. .
.
2. В реакции гидрирования ацетилена до этана концентрацию водорода увеличили в 6 раз, а концентрацию ацетилена уменьшили в 12 раз, поддерживая при этом температуру в системе постоянной. Определите, как изменилась скорость этой реакции.
Решение. В задаче речь идёт о реакции, которую условно можно принять за элементарную, одностадийную, гомогенную, протекающую по уравнению
 .
.
Применим
к этому процессу закон действующих
масс, обозначив через
 – скорость реакции в начальный момент
времени и через
– скорость реакции в начальный момент
времени и через – скорость реакции после изменения
концентраций реагирующих веществ. Тогда
получим:
– скорость реакции после изменения
концентраций реагирующих веществ. Тогда
получим:
 и
и
 .
.
Чтобы
узнать, как изменилась скорость реакции,
разделим
 на
на :
:

Следовательно, в результате изменения концентраций водорода и ацетилена скорость реакции возросла в 3 раза.
Ответ: скорость реакции возросла в 3 раза.
3. Скорость процесса окисления аммиака кислородом, протекающего по уравнению
 ,
,
увеличилась в 512 раз. Определите, как изменилось при этом давление в зоне реакции.
Решение.
Поскольку в реакции участвуют только
газообразные реагенты, то их концентрации
в объеме реакционного сосуда можно
заменить парциальными давлениями.
Применим к этому процессу закон
действующих масс, обозначив через Р̃
парциальное давление каждого из
компонентов в смеси, черезx– неизвестную величину, на которую
изменилось давление в системе, через – скорость реакции в начальный момент
времени и через
– скорость реакции в начальный момент
времени и через – скорость реакции после изменения
давления в системе. Тогда получим:
– скорость реакции после изменения
давления в системе. Тогда получим:
 и
и .
.
И далее
 .
Откуда
.
Откуда ;
; ;
; .
Следовательно, давление в системе было
увеличено в 2 раза.
.
Следовательно, давление в системе было
увеличено в 2 раза.
Ответ: давление увеличено в 2 раза.
4. Реакция между веществами подчиняется уравнению:
подчиняется уравнению: .
При начальных концентрациях реагентов
.
При начальных концентрациях реагентов и
и скорость этой реакции была равна
скорость этой реакции была равна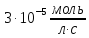 .
Определите константу скорости реакции
и установите, как изменится её скорость,
когда в реакционном пространстве
останется лишь
.
Определите константу скорости реакции
и установите, как изменится её скорость,
когда в реакционном пространстве
останется лишь вещества
вещества .
.
Решение. Запишем выражение закона
действующих масс, которому подчиняются
реагенты в этом химическом процессе:
в этом химическом процессе: .
По начальным концентрациям реагентов
и скорости реакции вычислим её константу
скорости:
.
По начальным концентрациям реагентов
и скорости реакции вычислим её константу
скорости:
 ,
и далее
,
и далее .
.
Для расчета скорости реакции
 через определённый промежуток времени
определим
через определённый промежуток времени
определим ,
если в сосуде осталось
,
если в сосуде осталось = 0,01 моль/л.
= 0,01 моль/л.
В реакцию вступили 0,02
 реагента
реагента т.к.
т.к. .
.
Из уравнения реакции видно, что вещества
 расходуется в 2 раза больше, следовательно,
расходуется в 2 раза больше, следовательно,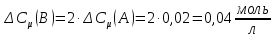 ,
и
,
и =
= 0,01
0,01 .
.
Отсюда

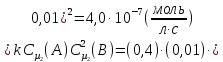 .
.
И тогда
 .
.
Ответ: скорость уменьшилась в 75 раз.
5. Через некоторое время после начала реакции, протекающей по уравнению
 ,
,
концентрации
участвующих в ней веществ стали равными
( ):
): ;
; ;
; .
Определите, какими были концентрации
хлороводорода и кислорода в начале
реакции, и как изменилась скорость этого
процесса, если объем реакционного
пространства оставался постоянным.
.
Определите, какими были концентрации
хлороводорода и кислорода в начале
реакции, и как изменилась скорость этого
процесса, если объем реакционного
пространства оставался постоянным.
Решение. Запишем уравнение закона
действующих масс для указанного процесса
окисления хлороводорода к моменту,
когда в системе уже образовалось 0,30
моль/л газообразного хлора: ,
и решим его:
,
и решим его:
 .
.
Начальные концентрации
 и
и
 будут больше
будут больше на величину израсходованного количества
вещества
на величину израсходованного количества
вещества и
и ,
затраченных на образование 0,30 моль/л
хлора. Уравнение реакции показывает,
что на образование 2 моль
,
затраченных на образование 0,30 моль/л
хлора. Уравнение реакции показывает,
что на образование 2 моль расходуется 4 моль
расходуется 4 моль и 1 моль
и 1 моль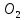 .
Следовательно, на образование 0,30 моль
.
Следовательно, на образование 0,30 моль потребуется
потребуется и
и .
Тогда начальные концентрации реагентов
будут равны (
.
Тогда начальные концентрации реагентов
будут равны ( ):
):
 ;
;
 .
.
В этих выражениях
 и
и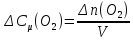 .
Поскольку объем системы
.
Поскольку объем системы неизвестен, его условно можно принять
равным 1 л.
неизвестен, его условно можно принять
равным 1 л.
Теперь рассчитаем начальную скорость реакции:

Отношение скоростей составит величину
 ,
что доказывает уменьшение скорости в
11,35 раза.
,
что доказывает уменьшение скорости в
11,35 раза.
Ответ: в начальный момент времени
концентрации реагентов были равны ( ):
): ;
; .
Скорость реакции уменьшилась в 11,35 раза.
.
Скорость реакции уменьшилась в 11,35 раза.
Пример 2. Определение порядка химической реакции и времени её протекания
1. Рассчитайте константу скорости реакции первого порядка, учитывая, что за 25 мин прореагировала четвертая часть участвующих в ней веществ.
Решение. Зависимость константы скорости реакции первого порядка от концентрации и времени протекания определяется уравнением:
 .
.
Пусть
начальная концентрация реагента
 ,
тогда через время
,
тогда через время его концентрация
его концентрация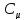 станет равной
станет равной .
Подставим значения
.
Подставим значения и
и в уравнение для
в уравнение для ,
переведя предварительно время в секунды,
и произведем вычисления:
,
переведя предварительно время в секунды,
и произведем вычисления:
 .
.
Ответ: константа скорости реакции
первого порядка .
.
2. Константа скорости реакции первого
порядка равна при начальной концентрации участвующих
в ней веществ, равной 1 моль/л. Определите,
какое количество вещества реагентов
останется не прореагировавшим через
10 ч после начала реакции.
при начальной концентрации участвующих
в ней веществ, равной 1 моль/л. Определите,
какое количество вещества реагентов
останется не прореагировавшим через
10 ч после начала реакции.
Решение. Преобразуем относительно уравнение зависимости константы скорости
реакции первого порядка от времени её
протекания и получим:
уравнение зависимости константы скорости
реакции первого порядка от времени её
протекания и получим:
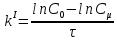 ,
далее
,
далее и окончательно
и окончательно .
.
Подставим в полученное выражение известные данные из условия задачи, преобразовав время в секунды, и произведем расчеты:
 .
отсюда
.
отсюда
Ответ: через 10 ч после начала реакции в системе останется не прореагировавшими 0,409 моль реагентов.
3. Реакция разложения иодоводорода
по уравнению
протекает
с константой скорости
 .
Рассчитайте время, за которое прореагирует
99% исходного вещества, если начальная
концентрация была равна 1
.
Рассчитайте время, за которое прореагирует
99% исходного вещества, если начальная
концентрация была равна 1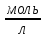 .
.
Решение. Уравнение химической реакции указывает на второй порядок зависимости скорости от концентрации. Связывающее их математическое выражение
 .
.
Преобразуем его относительно времени
τ:
 .
.
Подставим в полученное выражение
известные данные, имея в виду, что к
моменту времени τ не прореагировавшим
останется 1% иодоводорода, что соответствует
его молярной концентрации
 .
И тогда
.
И тогда
 .
.
Ответ: 99% иодоводорода прореагирует за 148,6 ч.
4. Изучение кинетики окислительно-восстановительной реакции, протекающей по уравнению
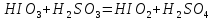 ,
,
показало, что её скорость пропорциональна концентрации каждого из реагентов в первой степени. Экспериментально получено, что при смешивании иодноватой и сернистой кислот с равными концентрациями, концентрация каждой из них через 40 с после начала опыта равнялась 0,25 моль/л, а через 60 с – 0,20 моль/л. Рассчитайте начальную концентрацию реагентов и константу скорости этой реакции.
Решение. В условии задачи указывается на второй порядок окислительно-восстановительной реакции, что подтверждает и само уравнение. Применим к нему выражение зависимости константы скорости от времени протекания реакции и концентрации:
 .
.
Поскольку константа скорости не зависит
от концентрации реагентов, то, используя
значения концентрации реагентов за
различные промежутки времени, мы получим
следующее уравнение:
 .
.
Решая это уравнение относительно
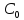 ,
получим:
,
получим: и далее
и далее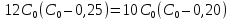 ,
откуда
,
откуда .
.
Найденное значение начальной концентрации
реагента
 подставим в выражение для
подставим в выражение для и найдем:
и найдем: .
.
Ответ: .
.
Пример 3. Вычисления зависимости скорости и константы скорости химической реакции от температуры по правилу Вант-Гоффа и уравнению Аррениуса. Расчеты энергии активации.
1. Определите, как изменится скорость реакции, протекающей в газовой фазе, если понизить температуру от 120 до 800С. Температурный коэффициент скорости этой реакции равен 3.
Решение. Для реакций, протекающих
в газовой фазе, понижение температуры
в реакционной среде приводит к уменьшению
скорости процесса. Следовательно, на
вопрос «как изменится скорость»
необходимо найти значение ,
где
,
где – скорости реакции при температурах
– скорости реакции при температурах .
.
Соотношение скоростей при различных температурах можно определить по уравнению Вант-Гоффа:
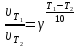 ,
где
,
где – температурный коэффициент Вант-Гоффа.
– температурный коэффициент Вант-Гоффа.
Подставим значения из условия задачи в данное уравнение и произведем расчеты:
 .
.
Ответ: скорость реакции уменьшилась в 81 раз.
2. Для реакции радиоактивного
превращения первого порядка установлено,
что период полураспада составляет с при 323 К и
с при 323 К и с при 353 К. Определите температурный
коэффициент константы скорости
радиоактивного разложения вещества.
с при 353 К. Определите температурный
коэффициент константы скорости
радиоактивного разложения вещества.
Решение.Зависимость константы
скорости реакции первого порядка от
периода полураспада вещества определяется
выражением .
.
А температурная зависимость константы
скорости реакции определяется
выражением
 .
.
Используя данные задачи, определим
значения константы скорости реакции
 и
и при температурах
при температурах и
и :
: ;
;
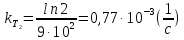 .
.
Тогда
 .
И далее:
.
И далее: и
и .
.
Ответ: температурный коэффициент реакции радиоактивного распада равен 1,88.
