ЛИНЕЙНАЯ АЛГЕБРА

1.Кольцо целых чисел. Теорема о делении с остатком.

Действительные числовые полукольца аддетивная полугруппа которых является группой называются кольцами. Множество таким образом является действительным кольцом которое мы называем кольцом целых чисел.

Деление c остатком – арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число.

Теорема (о делении с остатком): для любого целого а и целого существуют и единственные целые q и r, такие что .

Доказательство:

Докажем сначала существование деления с остатком. Рассмотрим все случаи, которые здесь могут представиться.

1) – любое целое число, . Рассмотрим множество всех чисел, кратных числа , и расположим его в порядке возрастания: . Пусть – наибольшее кратное числа , не превышающее . Тогда , но , то есть 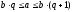, откуда . Положив , получим: , .

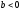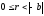2) – целое число, . Так как , то согласно случаю 1) деление на возможно, а это означает существование таких целых чисел и , что , , или , .

Теперь докажем единственность деления с остатком. Пусть деление на не единственно, то есть существуют два неполных частных и и два остатка и такие, что

Тогда , или , но так как , то равенство возможно лишь при условии . Следовательно, , но тогда 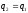. Единственность доказана.

Замечание 1. В частности, если 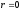, то и делится на .

Замечание 2. Если то q называется неполным частным, а r – остатком от деления a на b.

2.Простые числа. Бесконечность множества простых чисел. Каноническое разложение составного числа и его единственность.

Число назовем простым если . Множество всех простых натуральных чисел обозначают через . Простота – это характеристическое свойство наименьшего неединичного делителя любого натурального числа.

Целое положительное число р> 1 называется простым, если оно имеет ровно два положительных делителя: 1 и р. Целое положительное число m > 1 называется составным, если оно имеет по крайней мере один положительный делитель отличный от 1 и m. В соответствии с определениями все множество целых положительных чисел можно разбить на три подмножества: простые числа, составные числа, 1.

Замечание: существует единственное простое четное число – 2. Все остальные четные числа являются составными.

Перечислим свойства простых чисел.

Теорема 1: если р и р₁ – простые числа и рр₁, то р не делится на р₁ .

Теорема 2: если произведение нескольких целых чисел делится на простое число р, то по меньшей мере один из сомножителей делится на р.

Теорема 3: (основная теорема арифметики) всякое целое положительное число, отличное от единицы, может быть представлено в виде произведения простых сомножителей и притом единственным образом (с точностью до порядка следования сомножителей), т. е. каждое натуральное число n>1 представляется в виде , где - простые числа, причем такое преставление единственно с точностью до порядка следования сомножителей.

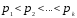Как следствие, каждое натуральное число n единственным образом представимо в виде , где - простые числа 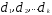и - некоторые натуральные числа. Такое представление числа n называется его каноническим разложением на простые сомножители.