3. Метод трапеций

Заменим площадь под кривой f(x) на отрезкеплощадью трапеции, тогда:

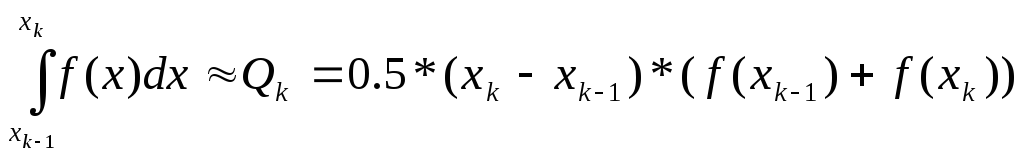(7.8)

Интеграл на всем интервале [a,b] при равномерном выборе шага

(7.9)

где . Погрешность этой формулы оценивается как:

, (7.10)

где . Заметим, что метод трапеций имеет погрешность несколько большую, чем метод средней точки.

Сделаем небольшие изменения в предыдущей подпрограмме-функции и запишем

function Q_Tr( a,b:real; n:longint): real;

var s,h:real; k:longint;

begin

h:=(b-a)/n; s:=0.5*(f(a)+f(b));

for k:=1 to n-1 do s:=s +f(a+h*k);

Q_Tr:=h*s

end;

4. Метод парабол

Заменим площадь под кривой f(x) на отрезкеплощадью под параболой. Парабола для своего описания требует трех соседних точек:

(7.11)

Значение функции в центральной точке включено в формулу с весом четыре, а двух крайних с весом единица. Интеграл на всем интервале [a,b] при равномерном выборе шага

(7.12)

Значения функций в нечетных узлах умножаются на коэффициент 4, а в четных – на 2. Крайние точки дают вклад в составную формулу (7.12), называемой формулой Симпсона, с единичным весом.

Оценка погрешности формулы Симпсона:

(7.13)

где .

Сделаем корректировку в подпрограмме-функции, составленной для метода трапеций

function Q_Sm( a,b:real; n:longint): real;

var s,h:real; k:longint;

begin

h:=(b-a)/n; s:=f(a)+f(b);

for k:=1 to n-1 do s:=s +f(a+h*k)*(k mod 2*2+2);

Q_Tr:=h*s/3

end;

В качестве теста возьмем интеграл В следующей таблице приведены результаты расчетов погрешностейдля квадратурных формул метода средней точки, трапецийи парабол.

kn

1 4 0.05234430595 0.10388110207 0.00455975498

2 8 0.01290908560 0.02576839806 0.00026916994

3 16 0.00321637817 0.00642965623 0.00001659105

4 32 0.00080341631 0.00160663903 0.00000103337

5 64 0.00020081172 0.00040161137 0.00000006453

6 128 0.00005020028 0.00010039981 0.00000000403

7 256 0.00001254989 0.00002509975 0.00000000025

8 512 0.00000313745 0.00000627494 0.00000000000

9 1024 0.00000078437 0.00000156871 0.00000000002

10 2048 0.00000019607 0.00000039220 0.00000000001

11 4096 0.00000004906 0.00000009793 0.00000000005

12 8192 0.00000001223 0.00000002455 0.00000000004

13 16384 0.00000000319 0.00000000619 0.00000000001

14 32768 0.00000000077 0.00000000132 0.00000000021

15 65536 0.00000000021 0.00000000038 0.00000000007

Эти результаты подтверждают теоретические выводы о том, что погрешности методов прямоугольников и трапеций пропорциональны , а метода парабол. Действительно, с уменьшением шага в два раза, величиныиуменьшаются приблизительно в четыре раза, в величина- в шестнадцать. Кроме того, можно сделать вывод о том, что погрешности округления с увеличением числа операций не так явно нарастают, как в методах численного дифференцирования, рассмотренных в предыдущей работе. Очевидно методы численного интегрирования более устойчивы и способны подавлять возникающие ошибки.