Лабораторная работа 5 Численное интегрирование

1. Введение

При вычислении площадей, объемов и решении многих других задач приходится сталкиваться с проблемой интегрирования. Если не удается аналитически выразить первообразную функцию или подынтегральная функция задана таблично, применяются приближенные и, в первую очередь, численные методы вычисления интегралов.

Идея численного интегрирования заложена в определении интеграла Римана от функции f(x):

, (7.1)

где (7.2)

интегральная сумма, - произвольная точка на частичном интервале,- длина интервала,, причем.

Интегральную сумму (7.2) называют квадратурной формулой; точки , в которых вычисляются значения функцииf(x), - узлами;- весами квадратурной формулы. Разностьявляется погрешностью квадратурной формулы, зависящей как от выбора весов, так и расположения узлов.

Разнообразные формулы численного интегрирования отличаются, главным образом, способом выбора узлов и весов. В этой работе будут рассмотрены методы прямоугольников, трапеций и парабол, построенные на равномерном выборе шаге h=const, способы их модификаций, а также алгоритмы вычисления интегралов со специально выбранными узлами и весами.

2. Метод прямоугольников

Заменим площадь под функцией f(x) на отрезкеплощадью прямоугольника, тогда интеграл на этом частичном отрезке легко вычисляется:

(7.3)

Часто это соотношение называется формулой средней точки. Интеграл на всем интервале [a,b] при равномерном выборе шага

(7.4)

Погрешность этой формулы

(7.5)

где . Такая квадратурная формула имеет второй порядок точности.

Если узлы расположены справа или слева, т.е.

; , (7.6)

то, из-за нарушения симметрии, погрешность этих формул становиться на порядок меньше

Составим подпрограмму-функцию:

functionQ_Mp(a,b:real;n:longint):real;

var s,h:real; k:longint;

begin

h:=(b-a)/n; s:=0;

for k:=1 to n do s:=s +f(a+h*(k-0.5));

Q_Mp:=h*s

end;

Заметим, что узлы на интервале [a,b] могут быть выбраны случайным образом. Проведяnвычислений со случайными узлами, усредним результат, который принимается за приближенное значение интеграла

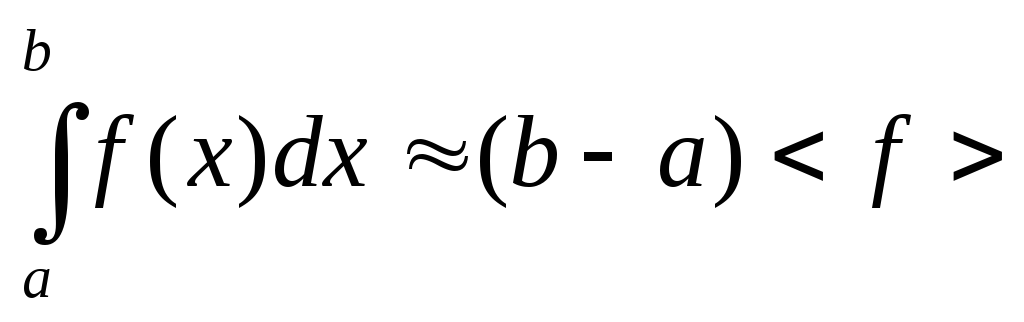, (7.7)

где - среднее на интервале [a,b] значение подынтегральной функции,. Здесь- случайное число, равномерно распределенное на интервале [0,1], которое можно моделировать на языкеTurboPascalс помощью датчикаRandom.

Погрешность такого статистического варианта метода прямоугольников, называемого еще методом Метрополиса (частного случая метода Монте-Карло), уменьшается с ростом числа испытаний по закону. Однако этот метод можно обобщить для вычисления кратных интегралов, а так же моделирования многих других задач.