Algebra_10kl_RU

РАЗДЕЛ 1. Тригонометрические функции

Значения функции косинус отрицательны (то есть абсцисса соответствую щей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях, поэто

му cos x < 0 при x (2π + 2πk; 32π + 2πk), k Z.

Промежутки возрастания и убывания.

(Учитывая периодичность функции cos x (T = 2π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной 2π, например на промежутке [0; 2π].

Если x [0; π] (рис. 59, а), то при увеличении аргумента x (x2 > x1) абсцисса соответствующей точки единичной окружности уменьшается (то есть

cos x2 < cosx1), следовательно, на этом промежутке функция cos x убывает. Учитывая периодичность функции cos x, делаем вывод, что она также убы вает на каждом из промежутков [2πk; π + 2πk], k Z.

Если x [π; 2π] (рис. 59, б), то при увеличении аргумента x (x2 > x1) абсцис са соответствующей точки единичной окружности увеличивается (то есть

cos x2 > cos x1), таким образом, на этом промежутке функция cos x возрас тает. Учитывая периодичность функции cos x, делаем вывод, что она воз растает также на каждом из промежутков [π + 2πk; 2π + 2πk], k Z. )

Проведенное исследование позволяет построить график функции y = cos x аналогично тому, как был построен график функции y = sin x. Но график функции у = cos x можно также получить с помощью геометрических преоб разований графика функции у = sin х, используя формулу

sin(2π + x)= cosx .

( Эту формулу можно обосновать, например, так. Рассмотрим единичную

окружность (рис. 60), отметим на ней точки А = Рх и B = Pπ2 +x , а также

62

§ 5. Свойства функций синуса, косинуса, тангенса и котангенса и их графики

tg(2π + x)= − ctgx . )

Учитывая, что cosx = sin(x + 2π ), график функции y = cos x можно полу чить из графика функции y = sin x его параллельным переносом вдоль оси Ох

на (− 2π ) (рис. 61). Полученный график называется косинусоидой (рис. 62).

Рис. 62

63

Напомним, что tgx = sinx . Таким образом, областью определения функ

cos x

ции y= tg x будут все значения аргумента, при которых cos х ≠ 0, то есть

64

§ 5. Свойства функций синуса, косинуса, тангенса и котангенса и их графики

получить и геометрически. Значение тангенса — это ордината соответствую щей точки Тх на линии тангенсов (рис. 63). Поскольку точки А и В единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы

не сможем найти значение тангенса для x = π + πk, k Z. Для всех других

2

значений аргумента мы можем найти соответствующую точку на линии тан

генсов и ее ординату — тангенс. Следовательно, все значения x ≠ π + πk вхо

2

дят в область определения функции у = tg х.

Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих точек на линии тангенсов принимают все значения от – до + . Поэтому областьзначенийфункции y = tg x — все действительные числа, то есть y R. Это можно записать так: E (tg x) = R. Отсюда следует, что

наибольшего и наименьшего значений функция tg x не имеет.

Как было показано в § 4, тангенс — нечетная функция: tg (–x) = –tg x, следовательно, ее график симметричен относительно начала координат.

Тангенс — периодическая функция с наименьшим положительным пери одом T = π: tg (x + π) = tg x (см. § 4). Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной π, а по том полученную линию перенести параллельно вправо и влево вдоль оси Ox на расстояния kT = πk, где k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oy значение x = 0. Тогда соответствующее значение y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при которых tg x, то есть ордината соответствующей точки линии танген сов, равна нулю. Это будет тогда и только тогда, когда на единичной окруж ности будут выбраны точки C или D, то есть при x = πk, k Z.

Промежутки знакопостоянства. Как было обосновано в § 4, значения функции тангенс положительны (то есть ордината соответствующей точки

65

РАЗДЕЛ 1. Тригонометрические функции

Промежутки возрастания и убывания.

( Учитывая периодичность функции tg x (период T = π), достаточно исследо вать ее на возрастание и убывание на любом промежутке длиной π, напри

мер, на промежутке (− 2π; 2π ). Если x (− 2π; 2π)(рис. 64), то при увеличении

аргумента x (x2 > x1) ордината соответствующей точки линии тангенсов увеличивается (то есть tg x2 > tg x1). Таким образом, на этом промежут ке функция tg x возрастает. Учитывая периодичность функции tg x, де лаем вывод, что она возрастает также на каждом из промежутков

(− 2π + πk; 2π + πk), k Z. )

Проведенное исследования позволяет обоснованно построить график функ ции y = tg x. Учитывая периодичность этой функции (с периодом π), сначала построим график на любом промежутке длиной π, например на промежутке

(− 2π; 2π ). Для более точного построения точек графика воспользуемся также

тем, что значение тангенса — это ордината соответствующей точки линии тангенсов. На рисунке 65 показано построение графика функции y = tg x

на промежутке (− 2π; 2π).

Рис. 66

66

§ 5. Свойства функций синуса, косинуса, тангенса и котангенса и их графики

Далее, учитывая периодичность тангенса (с периодом π), повторяем вид графика на каждом промежутке длиной π (то есть параллельно переносим график вдоль оси Ох на πk, где k — целое число).

Получаем график, приведенный на рисунке 66, который называется тан( генсоидой.

5.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК

Т а б л и ц а 13

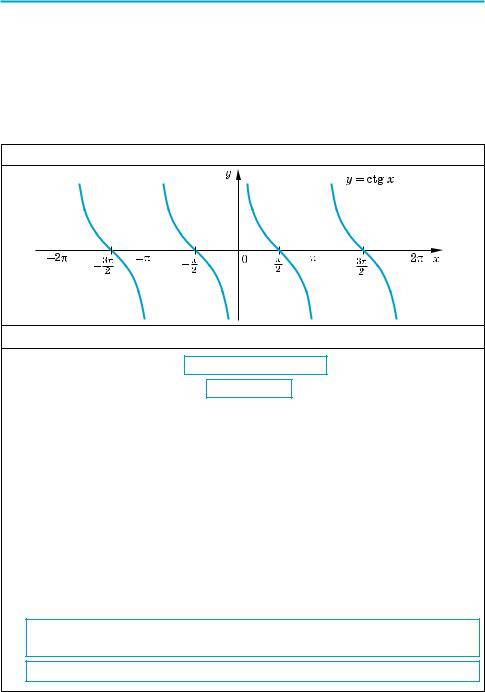
График функции y = ctg x (котангенсоида)

Свойства функции y = ctg x

1.Область определения: D (ctg x): x ≠ πk, k Z

2.Область значений: y R. E (ctg x) = R

3.Функция четная: ctg (–x) = –ctg x

7.Промежутки возрастания и убывания:

функция ctg x убывает на каждом из промежутков своей области определения, то есть на каждом из промежутков (πk; π + πk), k Z.

8.Наибольшего и наименьшего значений функция не имеет.

67

РАЗДЕЛ 1. Тригонометрические функции

Объяснение и обоснование

Так как ctgx = cos x , то областью определения котангенса будут все значе

sin x

ния аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k Z. Таким образом,

D (ctg x): x ≠ πk, k Z.

Тот же результат можно получить, используя геометрическую иллюстра цию. Значение котангенса — это абсцисса соответствующей точки на линии котангенсов (рис. 67). Поскольку точки А и В единичной окружности лежат на прямых ОА и ОВ, параллельных линии котангенсов, мы не можем найти зна чение котангенса для x = πk, k Z. Для других значений аргумента мы можем найти соответствующую точку на линии котангенсов и ее абсциссу — котан генс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.

Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все зна чения от – до + , таким образом, область значений функции y = ctg x — все действительные числа, то есть y R. Это можно записать так: E (ctg x) = R. Из приведенных рассуждений также вытекает, что наибольшего и наимень( шего значений функция ctg x не имеет.

Как было показано в § 4, котангенс — нечетная функция: ctg (–x) = –ctg x, поэтому ее график симметричен относительно начала координат.

Там же было обосновано, что котангенс — периодическая функция с наи меньшим положительным периодом T = π: ctg (x + π) = ctg x, поэтому через промежутки длиной π вид графика функции ctg x повторяется.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oy значение x = 0. Но ctg 0 не существует, значит, график функции y = ctg x не пересекает ось Oy.

На оси Оx значение y = 0. Поэтому необходимо найти такие значения x, при которых ctg x, то есть абсцисса соответствующей точки линии котанген сов, равна нулю. Это будет тогда и только тогда, когда на единичной окруж

ности будут выбраны точки C или D, то есть при x = π + πk, k Z.

68

§ 5. Свойства функций синуса, косинуса, тангенса и котангенса и их графики

Значения функции котангенс отрицательны (то есть абсцисса соответству ющей точки линии котангенсов отрицательна) во ІІ и ІV четвертях, таким образом, ctg x < 0 при x (2π + πk; π + πk), k Z.

Промежутки возрастания и убывания.

(Учитывая периодичность функции ctg x (наименьший положительный период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π, например на промежутке (0; π).

Если x (0; π) ( рис. 69), то при увеличении аргумента x (x2 > x1) абсцисса соответствующей точки линии котангенсов уменьшается (то есть

ctg x2 < ctg x1), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y = ctg x, делаем вывод, что она также убывает на каждом из промежутков (πk; π + πk), k Z. )

Проведенное исследование позволяет построить график функции y = ctg x

аналогично тому, как был построен график функции y = tg x. Но график функ

симметричным отображением полученного графика относительно оси Ох. Получаем график, который называется котангенсоидой (рис. 70).

Рис. 70

69

РАЗДЕЛ 1. Тригонометрические функции

Примеры решения задач

Задача 1 Постройте график функции и укажите нули функции и про межутки знакопостоянства: 1) у = 2 sin х; 2) у = sin 2х.

К о м м е н т а р и й Графики всех данных функций можно получить с помощью геометриче

ских преобразований графика функции f (x) = sin х (табл. 4). Таким образом, графиком каждой из этих функций будет синусоида, полученная для:

1)у = 2 sin х = 2 f (x) растяжением графика y = sin x вдвое вдоль оси Оу;

2)у = sin 2х = f (2x) сжатием графика y = sin x вдвое вдоль оси Ох.

Нули функции — это абсциссы точек пересечения графика с осью Ох. Чтобы записать промежутки знакопостоянства функции, заметим, что

функция у = 2sin х периодическая с периодом T = 2π, а функция у = sin 2х

периодическая с периодом T = 2π = π. Поэтому для каждой функции достаточ

2

но выяснить на одном периоде, где значения функции положительны (гра фик находится выше оси Ох) и где отрицательны (график находится ниже оси Ох), а потом полученные промежутки повторить через период.

Ре ш е н и е

1)X График функции у = 2 sin х получаем из графика функции у = sin х растяжением его вдвое вдоль оси Оу.

Нули функции: x = πk, k Z.

Промежутки знакопостоянства: 2 sin x > 0 при x (2πk; π + 2πk), k Z;

2sin x < 0 при x (π + 2πk; 2π + 2πk), k Z. Y

2)X График функции у = sin 2х получаем из графика функции у = sin х сжатием его вдвое вдоль оси Ох.

70

§ 5. Свойства функций синуса, косинуса, тангенса и котангенса и их графики

Нули функции: x = πk , k Z.

К о м м е н т а р и й Для расположения данных чисел в порядке их возрастания выясним, ка

кие из них положительны, а какие отрицательны, а затем сравним между собой отдельно положительные числа и отдельно отрицательные, учитывая известные промежутки возрастания и убывания функции sin х.

Р е ш е н и е

XЧисла sin 1,9 и sin 3 положительны, так как точки Р1,9 и Р3 находятся во II четверти. Числа sin (–1) и sin (–1,5) отрицательны, так как точки Р–1

возрастает. Учитывая, что –1 > –1,5, получаем sin (–1) > sin (–1,5). Таким образом, в порядке возрастания эти числа располагаются так:

sin (–1,5), sin (–1), sin 3, sin 1,9. Y

Задача 3 Постройте график функции: 1) у = | sin х |; 2) у = sin | х |.

К о м м е н т а р и й Графики данных функций можно получить с помощью геометрических пре

образований графика функции f (x) = sin х. Напомним соответствующие пре образования:

1)у = | sin х | = | f (x) | — выше оси Ox (и на самой оси) график функции y = sin x остается без изменений, часть графика, расположенная ниже оси Ox, ото бражается симметрично относительно оси Ox;

2)у = sin | х | = f (| x |) — справа от оси Oy (и на самой оси) график функции y = sin x остается без изменений, и эта же часть графика отображается сим метрично относительно оси Oy.

Р е ш е н и е

X Построим сначала график функции у = f (x) = sin х:

71