
Algebra_10kl_RU
.pdf
РАЗДЕЛ 1. Тригонометрические функции
Упражнения
1°. Изобразите угол, образованный поворотом луча OA около точки O на:
|
1) 270°; |
2) |
–270°; |
3) 720°; |
4) –90°; |
||||||||||||
|
5) 225°; |
6) –45°; |
7) 540°; |
8) –180°; |
|||||||||||||
|
9) 360°; |
10) –60°. |
|
|
|
|
|
|
|
|
|
||||||
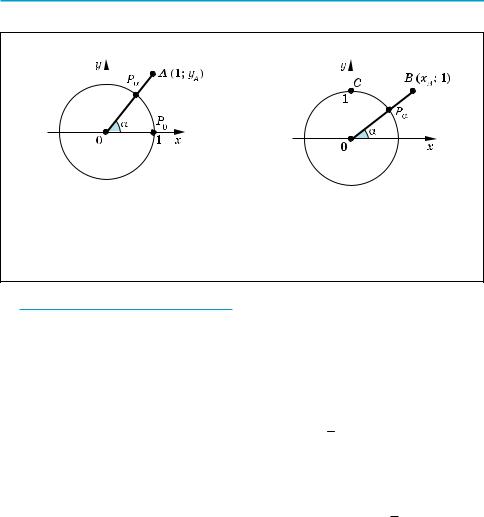
2°. Чему равны углы поворота, показанные на рисунке 32? |
|||||||||||||||||
3. |
Выразите в радианной мере величины углов: |
|
|
|
|||||||||||||
|
1°) 225°; |
2°) 36°; |
3) 100°; |
4) –240°; |
|||||||||||||
|
5) –22,5°; |
6) |
–150°. |
|
|
|
|
|
|
|
|
|
|||||
4. |
Выразите в градусной мере величины углов: |
|
|
|
|||||||||||||
|
1) 3π; |
2) |
|
3π |
; |
3) |
− |
2π |
; |
4) |
7π |
; |
|||||
|
|
|
|
|
4 |
|
|
|
5 |
|
6 |
|
|||||
|
5) − |
π |
; |
6) |
|
11π |
; |
7) |
− |
π |
; |
8) 3. |
|
||||
|
|
6 |
|
|
|
||||||||||||
|
18 |
|
|
|
|
|
8 |
|
|
|
|
|
|||||
5. |
С помощью калькулятора (или таблиц) найдите радианные меры углов: |
||||||||||||||||
|
1) 27°; |
|
2) 132°; |
3) 43°; |
|
4) 114°. |
|||||||||||
6. |
С помощью калькулятора (или таблиц) найдите градусные меры углов: |
||||||||||||||||
|
1) 0,5585; |
2) 0,8098; |
3) 3,1416; |
4) 4,4454. |
|||||||||||||
1) |
2) |
3) |
4) |
|
|
Рис. 32 |
|
42

§3 |
|
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ |
||
|
УГЛА И ЧИСЛОВОГО АРГУМЕНТА |
|
||
|
|
|
|
Т а б л и ц а 7 |
|
|
|
||
|
|
1. Опредение тригонометрических функций |
||
|
|
|
|
|
Через единичную |
Через произвольную |
Через прямоугольный |
||
окружность |
окружность |
треугольник |
||
|
(R = 1) |
(R — радиус окружности) |
(для острых углов) |
|
|
|
sin α = y |
— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
sinα= |
|
y |
|
|
|
sinα= a |
|
|||||||||||||
ордината точки P |
|
|
|
|
|
|
|||||||||||||||||
|
|
R |
|
||||||||||||||||||||
α |
|
|
|
|
|
|
|
c |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
cos α = x |
— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
cosα= |
x |
|
|
cosα= |
b |
|
||||||||||||||
абсцисса точки Pα |
|
|
|
||||||||||||||||||||
R |
c |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
tg α= |
y |
|
= sin α |
|
|
tg α= |
y |
|
|
|
tg α= a |
|
||||||||||
|
|
|
x |
cos α |
|
|
|
x |
|
|
b |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
cos α |
|
|
|
|
|
x |
|
|
|
|
|
|
|||||
|
ctg α = |
= |
|
|
|
|
|
|
|
|
b |
|
|||||||||||
|
|
|
|
|
|
|
ctg α= y |
|
|
ctg α= |
|
||||||||||||
y |
sin α |
|
|
||||||||||||||||||||
|
|
|
a |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Тригонометрические функции числового аргумента
sin (числа α ) = sin (угла в α радиан ) cos (числа α ) = cos (угла в α радиан ) tg (числа α ) = tg (угла в α радиан ) ctg (числа α ) = ctg (угла в α радиан )
43
РАЗДЕЛ 1. Тригонометрические функции
П р о д о л ж. т а б л. 7
3. Линии тангенсов и котангесов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
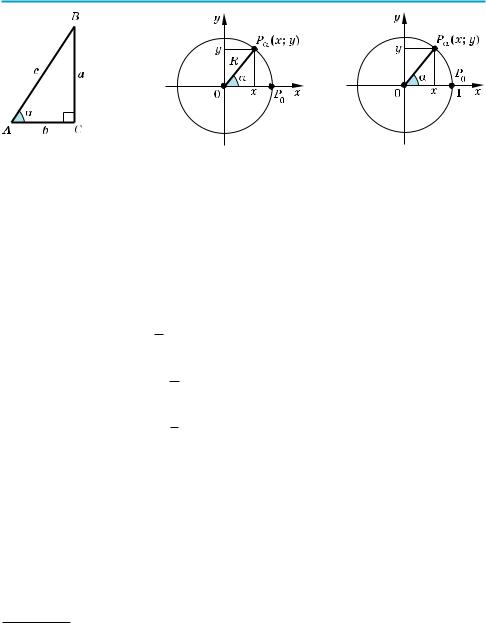
AP0 — линия тангенсов (AP0 C Oy) |
|
|
|
|
|
||
СВ — линия котангенсов (СВ C Oх) |
|||||||
tg α = yA — |
|
ctg α = xB — |
|||||
ордината соответствующей точки |
абсцисса соответствующей точки |
||||||
линии тангенсов |
|
линии котангенсов |
|||||
|
|
|
|
|
|
|
|
Объяснение и обоснование
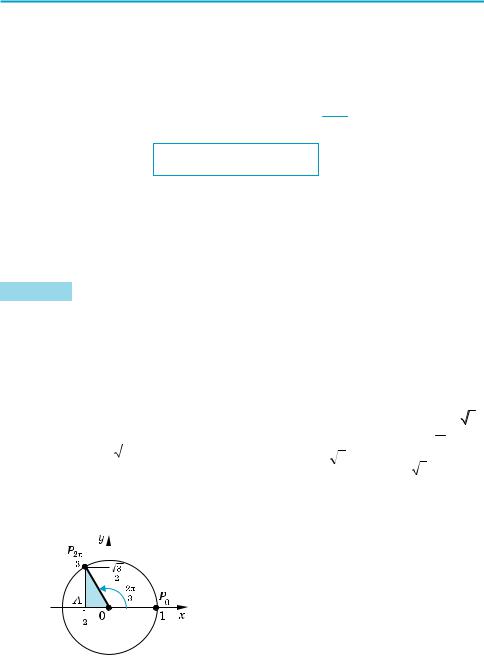
1. Определение тригонометрических функций. Из курса геометрии вам из вестно определение тригонометрических функций острого угла в прямоуголь ном треугольнике. Напомним их.
Синусом острого угла α в прямоугольном треугольнике называется отно
шение противолежащего катета к гипотенузе: sinα = a (рис. 33). c
Косинусом острого угла α в прямоугольном треугольнике называется от
ношение прилежащего катета к гипотенузе: cosα = b .
c
Тангенсом острого угла α в прямоугольном треугольнике называется от
ношение противолежащего катета к прилежащему: tg α = a . b
Котангенсом острого угла α в прямоугольном треугольнике называется
отношение прилежащего катета к противолежащему: ctg α = b . a
В курсе геометрии было обосновано, что синус и косинус острого угла зави сят только от величины угла и не зависят от длин сторон треугольника и его расположения, то есть синус и косинус (а таким образом, и тангенс, и котан генс) являются функциями угла, которые называются тригонометриче( скими функциями.
Также в курсе геометрии с использованием окружности с центром в начале координат было введено определение тригонометрических функций для уг лов от 0° до 180°. Эти определения можно применить для нахождения триго нометрических функций любых углов. Напомним их (но теперь будем рас сматривать любые углы α от – до + ).
44
§ 3. Тригонометрические функции угла и числового аргумента
Рис. 33 |
Рис. 34 |
Рис. 35 |
|
Возьмем окружность радиуса R с центром в начале координат. Обозначим точку окружности на положительной полуоси абсцисс через P0 (рис. 34). Необ ходимые нам углы будем образовывать поворотом радиуса OP0 около точки O. Пусть в результате поворота на угол α около точки O радиус OP0 займет поло жение OPα (говорят, что при повороте на угол α радиус OP0 переходит в ра диус OPα, а точка P0 переходит в точку Pα). Напомним, что при α > 0 радиус OP0 поворачивается против часовой стрелки, а при α < 0 — по часовой стрелке.
Пусть точка Pα имеет координаты (x; y). Тогда:
синусом угла α называется отношение ординаты точки Pα (x; y) окружно
сти к ее радиусу: sinα = Ry ;
косинусом угла α называется отношение абсциссы точки Pα (x; y) окруж
ности к ее радиусу: cosα = x ;
R
тангенсом угла α называется отношение ординаты точки Pα (x; y) окруж ности к ее абсциссе: tg α = xy (конечно, при x ≠ 0);
котангенсом угла α называется отношение абсциссы точки Pα (x; y) окруж ности к ее ординате: ctg α = xy (при y ≠ 0).
Как и для тригонометрических функций острых углов, значения sinα, cos α, tg α, ctg α зависят только от величины угла α и не зависят от радиуса R *. Удобно взять R = 1, что позволит несколько упростить приведенные определе ния тригонометрических функций.
Окружность радиуса 1 с центром в начале координат будем называть еди( ничной окружностью.
Пусть при повороте на угол α точка P0 (1; 0) переходит в точку Pα (x; y) (то есть при повороте на угол α радиус OP0 переходит в радиус OPα) (рис. 35).
* Это следует из того, что две концентрические окружности гомотетичны (центр гомоте тии — точка О, а коэффициент гомотетии k — отношение радиусов этих окружностей), тогда и точки Pα на этих окружностях также будут гомотетичны. Таким образом, при перехо де от одной окружности к другой в определениях тригонометрических функций числитель и знаменатель соответствующей дроби умножаются на k, а значение дроби не изменяется.
45
РАЗДЕЛ 1. Тригонометрические функции
Синусом угла α называется ордината точки Pα (x; y) единичной окружности: sin α = y.
Косинусом угла α называется абсцисса точки Pα (x; y) единичной окружности: cos α = x.
Тангенсом угла α называется отношение ординаты точки Pα (x; y) единич ной окружности к ее абсциссе, то есть отношение cossin αα .
Таким образом,
tg α = sinα (где cos α ≠ 0) . cosα
Котангенсом угла α называется отношение абсциссы точки Pα (x; y) еди
|
|
|
cosα |
ничной окружности к ее ординате, то есть отношение |
sinα . |
||
Таким образом, |
|
||
|
cosα (где sin α ≠ 0) |
. |
|
|
ctg α = sinα |
|
|
Пример Пользуясь этими определениями, найдем синус, косинус, тан
|
|
|
генс и котангенс угла |
|
2π |
радиан. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
2π |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
XРассмотрим единичную окружность (рис. 36). При повороте на угол |
|
ра |
||||||||||||||||||||||||||||
3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
диус OP0 переходит в радиус OP2π (а точка P0 переходит в точку P2π ). Коорди |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
наты точки P2π можно найти, используя свойства прямоугольного треуголь |
||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ника OAP |
|
(с углами 60° и 30° и гипотенузой 1): x = − OA = − |
1 |
; y = AP |
= |
|
3 |
. |
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2π |
|
2 |
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2π |
= y = |
3 |
|
2π |
= x = − |
1 |
|
|
2π |
= |
sin |
|
|
|
= − |
3; ctg |
2π |
= − |
1 |
. Y |
|
|
|
||||||
Тогда: sin |
; cos |
; |
tg |
3 |
|
|
|
|||||||||||||||||||||||
3 |
|
2 |
3 |
2 |
3 |
cos |
2π |
3 |
3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
Аналогично находятся значения синуса, косинуса, тангенса и котангенса углов, указанных в верхней строке таблицы 8.
|
|
|
|
|
|
|
|
|
|
Укажем, что таким образом можно |
|
|
|
|
|
|
|
|
|
|
найти тригонометрические функции |
|
|
|
|
|
|
|
|
|
|
тольконекоторыхуглов.Тригонометри |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ческие функции произвольного угла |
|
|
|
|
|
|
|
|
|
|
обычно находят с помощью калькуля |
|
|
|
|
|
|
|
|
|
|
тора или таблиц. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Тригонометрические функции чис |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лового аргумента. Введенные определе |
|
|
|
|
|
|
|
|
|
|
ния позволяют рассматривать не толь |
|
|
|
|
|
|
|
|
|
|
ко тригонометрические функции углов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 36 |
а и тригонометрические функции чис |
|||||
46

§ 3. Тригонометрические функции угла и числового аргумента
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а 8 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
градусы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
радианы |
|
|
π |
|
π |
|
|
π |
|
π |
|
|
3π |
|
||||
|
|
|
6 |
|
|
4 |
|
3 |
|
2 |
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
3 |
|
— |
|
|
|
|
— |
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
— |
|
3 |
|
|
|
|
|
3 |
|
|
|
— |
|
|
|
— |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ловых аргументов, если рассматривать тригонометрические функции числа α как соответствующие тригонометрические функции угла в α радиан. То есть:
синус числа α — это синус угла в α радиан; косинус числа α — это косинус угла в α радиан.
|
|
π |
= sin( |
π |
радиан)= sin30° = |
1 |
|
|
Например: sin |
(см. также пункт 2 табл. 7). |
|||||||
|
|
|
||||||
6 |
6 |
2 |
|
|||||
3. Линии тангенсов и котангенсов. Для решения некоторых задач полезно иметь представление о линиях тангенсов и котангенсов.
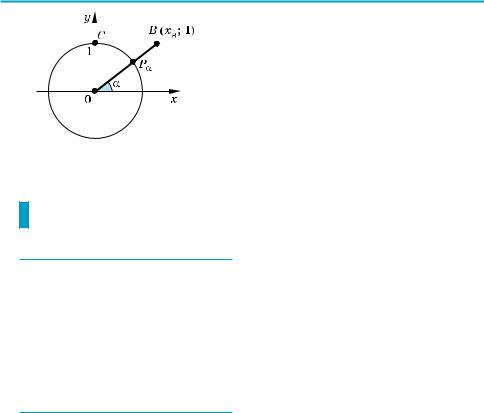
(Проведем через точку P0 единичной окружности прямую AP0, параллель ную оси Oy (рис. 37). Эта прямая называется линией тангенсов.
Пусть α — произвольное число (или угол), для которого cosα ≠ 0. Тогда
точка Pα не лежит на оси Oy и прямая OPα пересекает линию тангенсов в точке A. Поскольку прямая OPα проходит через начало координат, то ее
уравнение имеет вид y = kx. Но эта прямая проходит через точку Pα с коор динатами (cos α; sin α), значит, координаты точки Pα удовлетворяют урав нению прямой y = kx, то есть
sin α = k cos α. Отсюда |
|
Следовательно, прямая OPα имеет |
|
уравнение y = (tg α)x. Прямая AP0 |
|
имеет уравнение x = 1. Чтобы найти |
|
ординату точки A, достаточно в урав |
|
нение прямой OPα подставить x = 1. |
|
Получаем yA = tg α. Таким образом, |
|
тангенс угла (числа) α — это |
|
ордината соответствующей |
Рис. 37 |
точки на линии тангенсов. ) |
47
РАЗДЕЛ 1. Тригонометрические функции
|
|
|
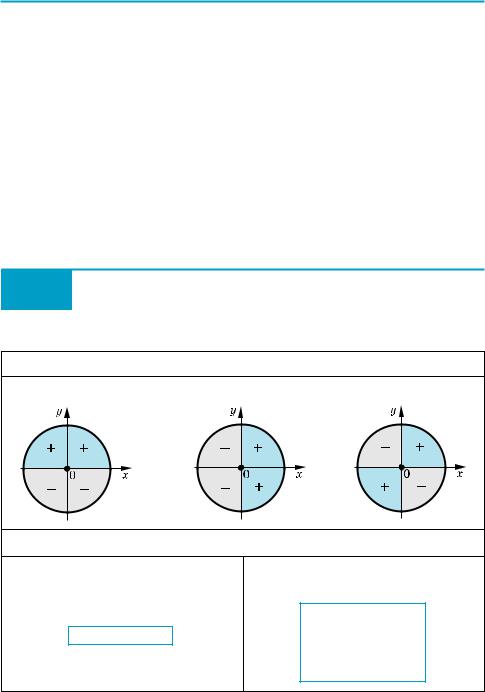
Аналогично вводится и понятие ли( |
|
|
|
нии котангенсов: это прямая CB |
|
|
|
(рис. 38), которая проходит через точ |
|
|
|
|
|
|
|
ку C (0; 1) единичной окружности па |
|
|
|
раллельно оси Ox. |
|
|
|
Если α — произвольное число (или |
|
|
|
угол), для которого sinα ≠ 0 (то есть |
|
|
|
точка Pα не лежит на оси Ox), то пря |
|
|
|
мая OPα пересекает линию котангенсов |
|
|
|
|
Рис. 38 |
в некоторой точке B (xB; 1). |
||
|
|
|
Аналогично вышеизложенному обо |
сновывается, что xB = ctg α, таким образом,
котангенс угла (числа) α — это абсцисса соответствующей точки на линии котангенсов.
Вопросы для контроля
1.Сформулируйте определения тригонометрических функций острого угла в прямоугольном треугольнике.
2.Сформулируйте определения тригонометрических функций произволь ного угла:
а) используя окружность радиуса R с центром в начале координат; б) используя единичную окружность.
3.Что имеют в виду, когда говорят о синусе, косинусе, тангенсе и котангенсе числа α?
Упражнения
1°. Постройте на единичной окружности точку Pα, в которую переходит точка P0 (1; 0) единичной окружности при повороте на угол α. В какой коорди натной четверти находится точка Pα в заданиях 3–6?
1) α = 3π; |
|
2) α = –4π; |
3) |
α = |
7π |
; |
||||
|
|
|||||||||
|
|
|
|
|
|
6 |
|
|
||
4) |
α = − 3π |
; |
5) |
α = 4π ; |
6) |
α = |
7π |
. |
||
|
||||||||||
|
4 |
|
|
3 |
|
4 |
|
|
||
2. Найдите значение sin α, cos α, tg α, ctg α (если они существуют) при:
1) α = 3π; |
2) α = –4π; |
3) |
α = − π ; |
|
|
|
|
|
2 |
4) |
α = 5π ; |
5*) α = − 5π ; |
6*) α = 3π . |
|
|
2 |
6 |
|
4 |
3°. Пользуясь определением синуса и косинуса, с помощью единичной окруж ности укажите знаки sin α и cos α, если:
1) |
α = 6π ; |
2) |
α = − π ; |
3) |
α = 5π ; |
||
|
5 |
|
6 |
|
6 |
||
4) |
α = − 2π ; |
5) |
α = |
π |
. |
|
|
|
|
|
|||||
|
3 |
|
10 |
|
|
|
|
48
|
|
|
§ 4. Свойства тригонометрических функций |
||
4*. Пользуясь линией тангенсов, укажите знак tg α, если: |
|||||
1) |
α = 4π ; |
|
2) |
α = − 3π ; |
3) α = 11π ; |
|
3 |
|
|
4 |
6 |
4) |
α = − 7π ; |
5) |
α = 9π . |
|
|
|
6 |
|
|
4 |
|
5*. Пользуясь линией котангенсов, укажите знак сtg α, если: |
|||||
1) |
α = − 4π ; |
2) |
α = 3π ; |
3) α = − 11π ; |
|
|
3 |
|
|
4 |
6 |
4) |
α = 7π ; |
|
5) |
α = − 9π . |
|
|
6 |
|
|
4 |
|
§4 |
СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ |
||||
|
|
|
|
|
Т а б л и ц а 9 |
|
|
|
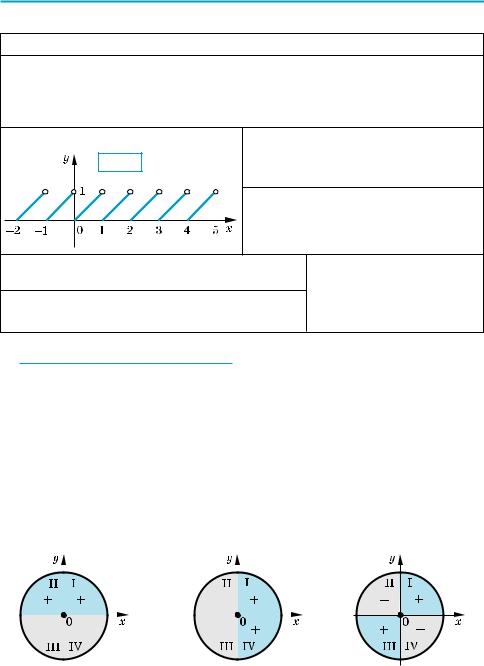
1. Знаки тригонометрических функций |
||
|
sin α |
|
|
cos α |
tg α, ctg α |
|
|
|
2. Четность и нечетность |
||
|
Косинус — четная функция |
Синус, тангенс и котангенс — |
|||
|
|
|
|
|
нечетные функции |
|
|
|
|
|
sin (–α) = –sin α |
|
cos (–α) = cos α |
|
tg (–α) = –tg α |
||
|
|
|
|
|
|
|
|
|
|
|
ctg (–α) = –ctg α |
|
|
|
|
49 |
|
РАЗДЕЛ 1. Тригонометрические функции |
||||
|
|
|
П р о д о л ж. т а б л. 9 |
|
|
3. Периодичность |
|
||
Функция f (x) называется периодической с периодом Т ≠ 0, если для |
||||
любых х из области определения функции числа (х + Т) и (х – Т) также |
||||
принадлежат области определения и выполняется равенство |
||||
|
f (x + Т) = f (x – Т) = f (x). |
|
||
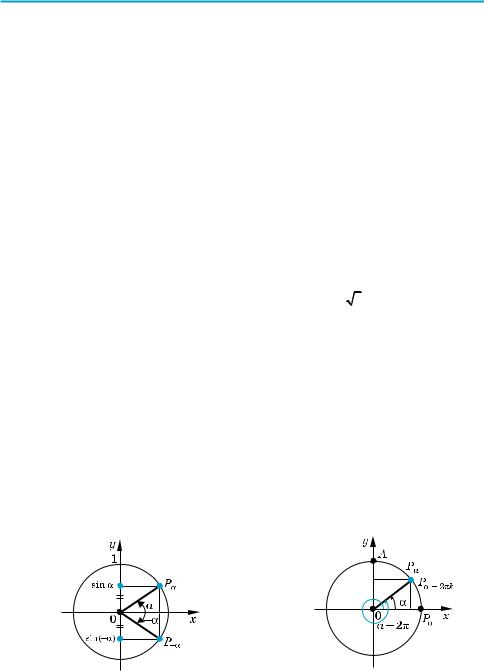
y = {x} — дробная часть числа x |
Через промежутки длиной Т |
|||
T = 1 |
|
(на оси Ох) вид графика периоди |
||
|
ческой функции повторяется |
|||
|
|
|||
|
|
Если Т — период функции, то ä Т, |
||
|
|
ä 2Т, ä 3Т, ..., ä kТ — также |
||
|
|
периоды этой функции (k N) |
||
sin (x + 2π) = sin x |
Функции sin x и cos x |
T = 2π — |
||
cos (x + 2π) = cos x |
имеют период T = 2π |
|||
общий период для всех |
||||
|
|
|
||
tg (x + π) = tg x |
Функции tg x и ctg x |
функций: |
||
ctg (x + π) = ctg x |
имеют период T = π |
sin x, сos x, tg x, ctg x |
||
Объяснение и обоснование |
|
|
||
1. Знаки тригонометрических функций легко определить, исходя из опреде ления этих функций.
(Например, sin α — это ордината соответствующей точки Pα единичной ок ружности. Поэтому значение sin α будет положительным, если точка Pα имеет положительную ординату, a это будет тогда, когда точка Pα находит
ся в I или II четверти (рис. 39). Если точка Pα находится в III или IV четвер ти, то ее ордината отрицательна, и поэтому sin α тоже отрицателен.
Аналогично, учитывая, что cos α — это абсцисса соответствующей точки Pα, получаем, что cos α > 0 в I и IV четвертях (абсцисса точки Pα положительна) и cos α < 0 во II и III четвертях (абсцисса точки Pα отрицательна) (рис. 40).
|
|
|
|
sin α |
|
|
|
cos α |
|||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 39 |
Рис. 40 |
tg α, ctg α |
Рис. 41 |
50
§ 4. Свойства тригонометрических функций
Поскольку tgα = |
sinα |
и ctgα = |
cos α |
, то tg α > 0 и ctg α > 0 там, где sin α и cos α |
|
cosα |
sin α |
||||
|
|
|
имеют одинаковые знаки, то есть в I и III четвертях, tg α < 0 и ctg α < 0 там,
где sin α и cos α имеют разные знаки, то есть во II и IV четвертях (рис. 41). )
2. Четность и нечетность тригонометрических функций.
(Чтобы исследовать тригонометрические функции на четность и нечетность,
заметим, что на единичной окружности точки Pα и P–α расположены сим метрично относительно оси Ox (рис. 42). Следовательно, эти точки имеют
одинаковые абсциссы и противоположные ординаты. Тогда cos(−α )= xP−α = xPα = cosα, sin(−α )= yP−α = −yPα = − sinα.
Таким образом, cos x — четная функция, а sin x — нечетная.
Тогда tg(−α ) = |
sin(−α ) |
|
= − sinα = − tgα; |
ctg(−α ) = |
cos(−α ) |
|
= |
cos α |
= − ctgα. |
|
cos (−α ) |
sin(−α ) |
− sinα |
||||||||
|
cos α |
|
|
|
||||||
Поэтому tg x и ctg x — нечетные функции. )
Четность и нечетность тригонометрических функций можно применять
для вычисления значений тригонометрических функций отрицательных углов (чисел).
Например, X sin(− |
π |
)= − sin |
π |
= − |
1 |
, cos(− |
π |
)= cos |
π |
= |
2 |
. Y |
|
|
|
|
|||||||||
6 |
6 |
2 |
4 |
4 |
|
2 |
|
|||||
3. Периодичность тригонометрических функций. Множество процессов и явлений, которые происходят в природе и технике, имеют повторяющийся характер (например, движение Земли вокруг Солнца, движение маховика). Для описания процессов такого рода используют так называемые периоди ческие функции.
Функция y = f (x) называется периодической с периодом T ≠ 0, если для
любого x из области определения функции числа (x + T) и (x – T) также принадлежат области определения и выполняется равенство
f (x + T) = f (x – T) = f (x).
(Учитывая, что на единичной окружности числам (углам) α и α + 2πk, где k Z, соответствует одна и та же точка (рис. 43), получаем
sin (α + 2πk) = = sin α, cos (α + 2πk) = cos α. Тогда 2πk (k ≠ 0) является периодом функций sin x и cos x.
Рис. 42 |
Рис. 43 |
51
