
Algebra_10kl_RU
.pdf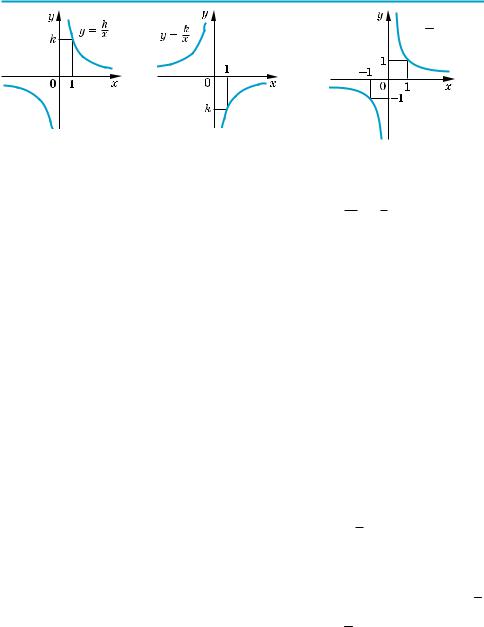
РАЗДЕЛ 1. Тригонометрические функции
y = 1 x
(k > 0) |
(k < 0) |
|
а |
б |
Рис. 15 |
Рис. 16 |
Функция нечетная, поскольку ее областью определения является множе
ство, симметричное относительно точки О, и f (−x) = k = − k = −f (x). Таким
−x x
образом, ее график симметричен относительно начала координат (рис. 15).
Возрастание и убывание функции зависит от знака коэффициента k.
(Если х2 > х1 (то есть х2 – х1 > 0), то для сравнения значений f (х2) и f (х1) рассмотрим их разность:
f (x ) − f (x ) = |
k |
− |
k |
= |
kx1 − kx2 |
= |
−k(x2 |
− x1 ) |
|
|
|
|
|
|
|
. |
(1) |
||||||
2 |
1 |
x2 |
|
x1 |
|
x1x2 |
|
|
|||
|
|
|
|
|
x1x2 |
|
|||||
На промежутке (0; + ) значение х1 > 0 и х2 > 0, следовательно, х1х2 > 0. На промежутке (– ; 0) значение х1 < 0 и х2 < 0, значит, х1х2 > 0. Учитывая, что х2 – х1 > 0 на каждом из промежутков (– ; 0) или (0; + ) при k > 0 из равенства (1) получаем f (х2) – f (х1) < 0, а при k < 0 получаем
f (х2) – f (х1) > 0.
При k > 0 на каждом из промежутков (– ; 0) и (0; + ), если х2 > х1, то
f(х2) < f (х1), таким образом, функция убывает на каждом из этих проме жутков.
При k < 0 на каждом из промежутков (– ; 0) и (0; + ), если х2 > х1, то
f(х2) > f (х1), следовательно, функция возрастает на каждом из этих про
межутков.)
Из курса алгебры известно, что график функции y = k (k ≠ 0) называется x
гиперболой (она состоит из двух ветвей). При k > 0 ветви гиперболы находят ся в І и ІІІ координатных четвертях, а при k < 0 — во ІІ и ІV четвертях (рис. 15).
З а м е ч а н и е. Характеризируя возрастание или убывание функции y = k
x
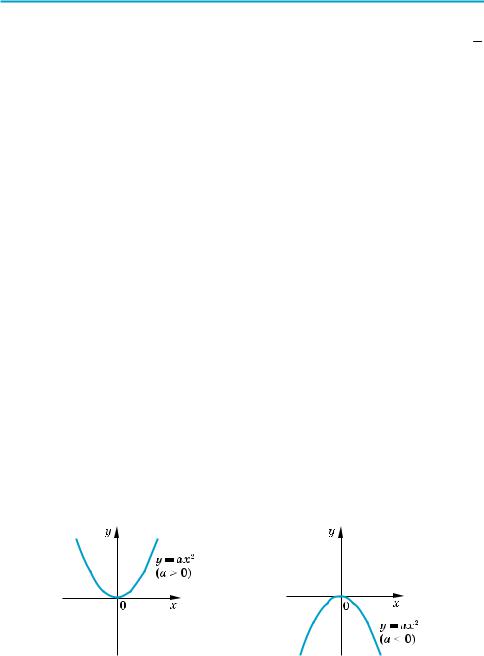
(k ≠ 0), следует помнить, что, например, функция y = 1 (рис. 16) убывает на
x
каждом из промежутков (–×; 0) и (0; +×), но на всей области определения (х ≠ 0) эта функция не является убывающей (и не является возрастающей). Действительно, если взять х1 = –1 и х2 = 1, то x2 > x1, но f (x2) = f (1) = 1,
22
§1. Повторение и расширение сведений о функции
аf (x1) = f (–1) = –1, то есть большему значению аргумента не соответствует
меньшее значение функции, и на всей ее области определения функция f (x) = 1
не является убывающей. |
|
x |
|
|
|
||
Поэтому же нельзя сказать, что функция f (x) = |
1 |
убывает при |
|
x |
|||
х (–×; 0) (0; +×). |
|
||
|
|
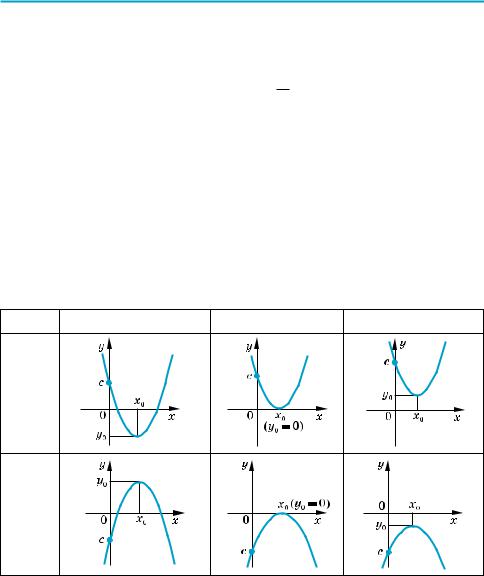
3. Функция у = ах2 (а ≠ 0). Как известно из курса алгебры, графиком этой функции является парабола, ветви которой направлены вверх при а > 0 (рис. 17, а) и вниз при а < 0 (рис. 17, б). Поскольку при х = 0 значение у = 0, то график всегда проходит через начало координат.
Область определения: х R, поскольку значение у = ах2 можно вычис лить при любых значениях х.
Функция четная, поскольку f (–x) = а(–х)2 = ах2 = f (x). Таким образом, ее график симметричен относительно оси Оу.
Для описания других свойств воспользуемся графиком функции у = ах2 (рис. 17). Эти свойства можно обосновать, опираясь на свойства функции у = х2 и на геометрические преобразования ее графика, которые будут рассмот рены далее в п. 1.3.
Область значений. При а > 0 график проходит через начало координат, а все остальные его точки находятся выше оси Ох. Если значение х увеличи вается до бесконечности, то и значение у также увеличивается до бесконечно сти (+ ), таким образом, у 0, то есть Е (у) = [0; + ).
Аналогично при а < 0 график также проходит через начало координат, но все остальные его точки находятся ниже оси Ох. Если значение х увеличи вается до бесконечности, то значение у уменьшается до минус бесконечности (– ), таким образом, у 0, то есть Е (у) = (– ; 0].
Возрастание и убывание. При а > 0 на промежутке (– ; 0] функция убы вает, а на промежутке [0; + ) — возрастает.
При а < 0 на промежутке (– ; 0] функция возрастает, а на промежутке [0; + ) — убывает.
Соответствующие графики приведены также в таблице 2.
а |
б |
Рис. 17
23
РАЗДЕЛ 1. Тригонометрические функции
4. Квадратичная функция y = ax2 + bx + c (a ≠ 0). Из курса алгебры 9 класса известно, что функция вида y = ax2 + bx + c, где a, b, c — действительные числа, причем a ≠ 0, называется квадратичной. Ее графиком является пара бола, ветви которой направлены вверх при а > 0 и вниз при а < 0.
Абсцисса вершины этой параболы x0 = − b . Для обоснования этого доста
2a
точно в заданном квадратном трехчлене выделить полный квадрат:
y = ax2 + bx + c = a(x2 + |
b |
x + |
c |
)= a(x + |
b |
)2 |
+ 4ac − b2 |
, то есть |
|||||
|
|
2a |
|||||||||||
|
a |
|
a |
|
|
4a |
|
|
|
||||
y = ax2 + bx + c = a(x + |
b |
)2 |
+ y , где y = 4ac − b2 |
= − |
D |
|
|||||||
|
|
||||||||||||
|
|
|
2a |
|
|
|
o |
o |
4a |
|
4a |
||
|
|
|
|
|
|
|
|
|
|
||||
(D = b2 – 4ac — дискриминант квадратного трехчлена ax2 + bx + c). Напомним, что в зависимости от знака дискриминанта D парабола или
пересекает ось Ох (D > 0), или не пересекает (D < 0), или касается ее (D = 0).
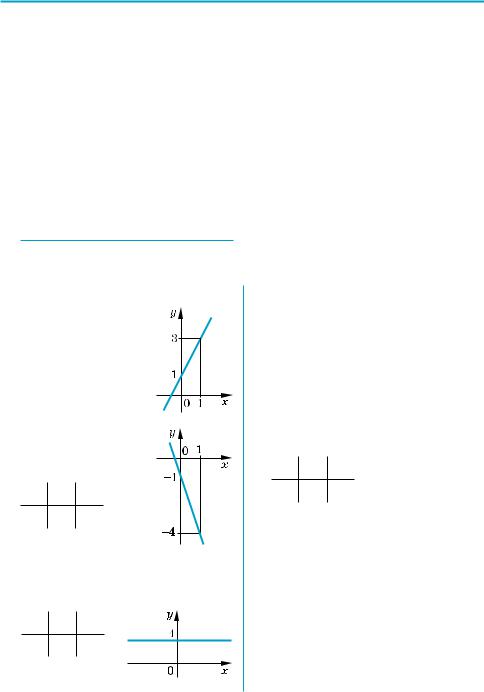
Основные варианты расположения графика функции y = ax2 + bx + c (a ≠ 0) представлены в таблице 3.
Т а б л и ц а 3
D > 0 |
D = 0 |
D < 0 |
а > 0
а < 0
Охарактеризуем свойства функции y = ax2 + bx + c (a ≠ 0), опираясь на эти известные нам графики.
Область определения: D (у) = R, поскольку значение y = ax2 + bx + c (a ≠ 0) можно вычислить при любых значениях х.
Область значений. При а > 0 функция принимает все значения у у0, то есть Е (у) = [у0; + ).
24
§ 1. Повторение и расширение сведений о функции
При а < 0 функция принимает все значения у уо , то есть Е (у) = (– ; уо]. Четность и нечетность. При b = 0 получаем четную квадратичную функ
цию у = ϕ (х) = ax2 + c. Действительно, ϕ (–х) = a(–x)2 + c = ax2 + c = ϕ (х).
В общем случае (если b ≠ 0) функция y = f (x) = ax2 + bx + c (a ≠ 0) не является ни четной, ни нечетной, поскольку
f (–x) = a(–x)2 + b(–x) + c = ax2 – bx + c ≠ f (x) (и не равно –f (x)).
Возрастание и убывание. При а > 0 на промежутке (– ; хо] функция убы вает, а на промежутке [х0; + ) — возрастает.
При а < 0 на промежутке (– ; х0] функция возрастает, а на промежутке
[х0; + ) — убывает.
Поскольку при х = 0 значение у = с, то график всегда пересекает ось Оу в точке с.
Соответствующие графики при D > 0 приведены также в таблице 2.
Примеры решения задач
Задача 1 |
Постройте график функции: |
|
1) у = 2х + 1; 2) у = –3х – 1; 3) у = 4. |
Р е ш е н и е
1) X График функции у = 2х + 1 — прямая.
x |
0 |
1 |
|
|
|
y |
1 |
3 |
|
|
|
Y
2) X График функции у = –3х – 1 — прямая.
x 0 1
y –1 –4
Y
3)X График функции у = 4 — пря мая, параллельная оси Ох, которая проходит через точку 4 на оси Оу.
x 0 1
y 4 4
Y
К о м м е н т а р и й
Все данные функции линейные, поэтому их графиками являются пря мые.
Чтобы построить прямые в зада ниях 1 и 2, достаточно построить две точки этих прямых. Например, мож но взять х = 0 и х = 1 и найти соответ ствующие значения у. Оформлять эти вычисления удобно в виде таблички:
x 0 1
y
В задании 3 рассматривается част ный случай линейной функции (у = b). Для построения этого графи ка полезно помнить, что прямая у = 4 — это прямая, параллельная оси Ох (при любом значении х значе ние у равно 4).
25
|
РАЗДЕЛ 1. Тригонометрические функции |
||||
|
|
|
|
|
|
Задача 2* |
По приведенному графику функции |
|
|
||
|
|||||
|
y = kx + b укажите знаки k и b. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Р е ш е н и е
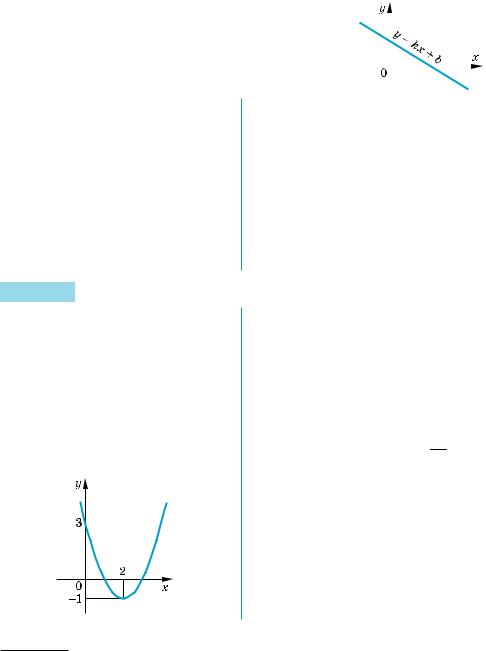
XПри х = 0 значение y = b. Посколь ку изображен график убывающей ли нейной функции, то k < 0.
Ответ: b > 0, k < 0.Y
К о м м е н т а р и й
График функции y = kx + b — пря мая, пересекающая ось Оу в точке b. На рисунке эта точка лежит выше нуля, таким образом, b > 0.
Линейная функция y = kx + b при k > 0 возрастающая, а при k < 0 — убывающая. На рисунке изображен график убывающей функции, следо вательно, k < 0.
Задача 3 Постройте график функции у = х2 – 4х + 3*.
Р е ш е н и е
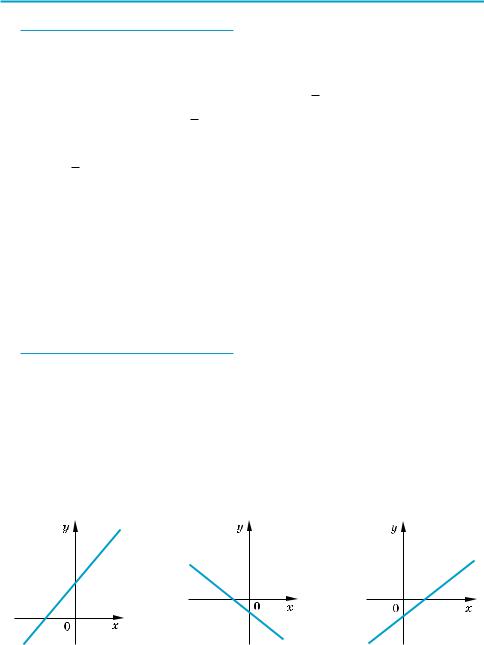
XГрафик заданной функции — пара бола (вида у = х2), ветви которой на правлены вверх.
Абсцисса вершины:
x |
= − |
b |
= − |
−4 |
= 2 . |
|
|
||||
0 |
2a |
|
2 1 |
||
|
|
|
|||
Тогда у0 = у (2) = 22 – 4æ2 + 3 = –1, и график имеет вид:
Y
К о м м е н т а р и й
Функция у = х2 – 4х + 3— квадра тичная (имеет вид у = aх2 – bх + с, где а ≠ 0). Таким образом, ее графиком будет парабола (вида у = aх2), ветви которой направлены вверх (а = 1> 0).
Абсцисса вершины параболы вы
числяется по формуле x0 = − 2ba, а ор
дината у0 — это соответствующее зна чение заданной функции при х = х0,
то есть у0 = у (х0).
Если необходимо уточнить, как проходит график, то можно найти координаты нескольких дополни тельных точек, например, при х = 0 получаем у = с = 3.
* Построение таких графиков с помощью геометрических преобразований графика функции у = х2 будет рассмотрено в пункте 1.3.
26
§ 1. Повторение и расширение сведений о функции
Вопросы для контроля
1.Какая функция называется линейной? Назовите свойства линейной функции. Какая линия является графиком линейной функции? Приве дите примеры линейных функций и их графиков.
2.Какая линия является графиком функции y = xk (k ≠ 0)? Приведите приме ры графиков функций y = xk при k > 0 и при k < 0. По графикам укажите свойства этой функции при k > 0 и при k < 0. Докажите нечетность функ
ции y = k (k ≠ 0). x
3.Какая линия является графиком функции у = aх2 (а ≠ 0)? Как расположен этот график при а > 0 и при а < 0? Приведите примеры графиков функций
у = aх2 при а > 0 и при а < 0. По графикам укажите свойства этой функции при а > 0 и при а < 0. Докажите четность функции у = aх2 (а ≠ 0).
4.Какая линия является графиком функции у = aх2 + bх + с (а ≠ 0)? Как
расположен график при а > 0 и при а < 0? Как найти абсциссу вершины графика функции у = aх2 + bх + с (а ≠ 0)? Приведите примеры графиков этой функции при а > 0 и при а < 0. По графикам укажите свойства этой функции при а > 0 и при а < 0.
Упражнения
1°. Постройте график функции:
1) у = 3х – 2; 2) у = –х + 4; 3) у = –2; 4) у = –5х; 5) у = 0; 6) у = 4х . Есть ли среди этих функций четные или нечетные? Ответ обоснуйте.
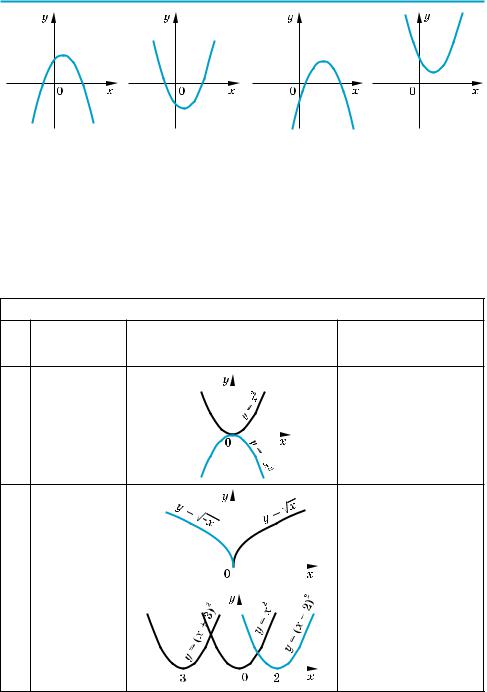
2*. По приведенным графикам функций y = kx + b (рис. 18) укажите знаки k и b в каждом случае.
Постройте график функции (3–5).
3°. |
1) |
y = − 2 |
; |
2) |
y = 3 |
; |
3) |
y = − 1 |
; |
4) |
y = 5 . |
|
|
x |
|
|
x |
|
|
x |
|
|
x |
4°. |
1) у = –2х2; |
2) у = 3х2; |
3) у = –3х2; |
4) у = 5х2. |
|||||||
1) |
2) |
3) |
Рис. 18
27
РАЗДЕЛ 1. Тригонометрические функции
1) |
2) |
3) |
4) |
|
|
Рис. 19 |
|
5. 1) у = х2 – 6х + 7; 2) у = –х2 + 4х + 2; 3) у = 2х2 – 2х + 1; 4) у = –3х2 + 6х. 6*. По приведенным графикам функции y = ax2 + bx + c (a ≠ 0) (рис. 19) ука
жите знаки a, b и c в каждом случае.
1.3.ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ С ПОМОЩЬЮ ГЕОМЕТРИ7 ЧЕСКИХ ПРЕОБРАЗОВАНИЙ ИЗВЕСТНЫХ ГРАФИКОВ ФУНКЦИЙ
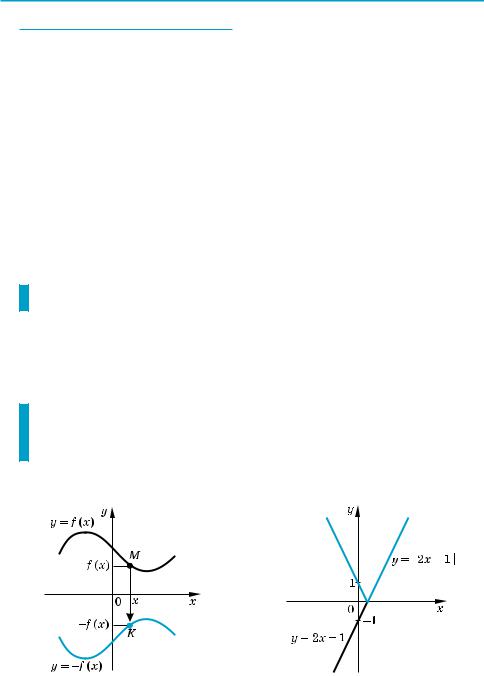
Т а б л и ц а 4
Преобразование графика функции y = f (x)
№ |
Формула |
Пример |
Преобразование |
|
зависимости |
||||
|
|
|
||
|
|
|
|
|
1 |
2 |
3 |
4 |
1 |
y = –f (x) |
|
|
Симметрия относи |
|
|
тельно оси Ох |
||
|
|
|
|
|
|
|
|
|
|
2 |
y = f (–x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Симметрия относи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельно оси Оу |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параллельный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
переноc графика |
3 |
y = f (x – a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции y = f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вдоль оси Ох на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а единиц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28

§ 1. Повторение и расширение сведений о функции
|
|
|
П р о д о л ж. т а б л. 4 |
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
Параллельный |
4 |
y = f (x)+с |
|
|
|
|
переноc графика |
|
|
|
|
функции y = f (x) |
||
|
|
|
|
|
|
вдоль оси Оу на |
|
|
|
|
|
|
c единиц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Растяжение или |
5 |
y = kf (x) |
|
|
|
|
|
|
|
|
сжатие вдоль оси Оу |
|
|
|
|
|
|
|
|
(при k > 1растяже |
||
|
(k > 0) |
|
|
|
|
|
|
|
|
ние, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
при 0 < k < 1 — |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сжатие) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Растяжение или |
|
y = f (αx) |
|
|
сжатие вдоль |
6 |
|
|
оси Ох |
|
|
(α > 0) |
y = |
1 x |
(при α > 1 сжатие, |
|
|
|
2 |
при 0 < α < 1 — |
|
|
|
|
растяжение) |
|
|
|
|
|
|
|
|
|
|
|
Выше оси Ох (и на |
|
y = |
|
|
|
|
|
|
|
|
|
самой оси) график |
7 |
|
f (x) |
|
|
|
|
|
|
|
функции y = f (x) — |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
без изменений, ниже |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оси Ох — симметрия |
|
|
|
|
|
|
|
|
|
|
|
относительно оси Ох |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Справа от оси Оу |
|
|
|
(и на самой оси) — |
|
8 |
y = f (| x |) |
без изменений, и эта |
|
же часть графика — |
|||
|
|
||
|
|
симметрия относи |
|
|
|
тельно оси Оу |
|
|
|
29 |
РАЗДЕЛ 1. Тригонометрические функции
Объяснение и обоснование
Рассмотрим способы построения графиков функций с помощью геометри ческих преобразований известных графиков функций.
1. Построение графика функции y = –f (x). Сравним графики функций y = x2
и y = –x2 (см. первую строку табл. 4). Очевидно, что график функции y = –x2 можно получить из графика функции y = x2 симметричным отображением его относительно оси Ox. Покажем, что всегда график функции y = –f (x) можно получить из графика функции y = f (x) симметричным отображением относи тельно оси Ox.
(Действительно, по определению график функции y = f (x) состоит из всех точек M координатной плоскости, которые имеют координаты (x; y) = (x; f (x)). Тогда график функции y = –f (x) состоит из всех точек K координатной плоскости, имеющих координаты (x; y) = (x; –f (x)).
Точки M (x; f(x)) и K (x; –f (x)) расположены на координатной плоскости симметрично относительно оси Ox (рис. 20). Таким образом, каждая точ ка K графика функции y = –f (x) получается симметричным отображением относительно оси Ox некоторой точки M графика y = f (x). Поэтому
график функции y = –f (x) можно получить из графика функции y = f (x) его симметричным отображением относительно оси Ox. )
Это свойство позволяет легко обосновать построение графика функции y = | f (x) |. Имеем:
y = |
|
f (x) |
f (x) при f (x) 0 (график не меняется); |
|
= |
||
|
|
|
−f (x) при f (x) < 0 (симметрия относительно оси Ox). |
Следовательно,
график функции y = | f (x) | может быть построен так: часть графи ка функции y = f (x), лежащая выше оси Ox (и на самой оси), остает ся без изменений, а часть, лежащая ниже оси Ox, отображается сим метрично относительно этой оси.
Например, на рисунке 21 и в таблице 4 (строка седьмая) с использованием этого правила изображен график функции y = | 2х – 1 |.
Рис. 20 |
Рис. 21 |
30

§1. Повторение и расширение сведений о функции
2.Построение графика функции y = f (–x).
(Для построения графика функции y = f (–x) учтем, что в определении гра фика функции первая координата для точек графика выбирается произ вольно из области определения функции. Если выбрать как первую коор динату значение (–x), то график функции y = f (–x) будет состоять из всех точек T координатной плоскости с координатами (–x; y) = (–x; f (x)). На помним, что график функции y = f (x) состоит из всех точек M (x; f (x)).
Точки M (x; f (x)) и T (–x; f (x)) расположены на координатной плоскости симметрично относительно оси Oy (рис. 22). Таким образом, каждая точка T графика функции y = f (–x) получается симметричным отображением от носительно оси Oy некоторой точки M графика функции y = f (x). Поэтому
график функции y = f (–x) можно получить из графика функции y = f (x) его симметричным отображением относительно оси Oy. )
Эта свойство позволяет легко обосновать построение графика функции y = f (| x |). Имеем:
( ) f (x) при x 0 (график не меняется);
y = f x = f (−x) при x < 0 (симметрия относительно оси Oy).
Следовательно, для того чтобы получить график функции y = f (| x |) при x < 0 (то есть слева от оси Oy), необходимо отобразить симметрично относительно оси Oy ту часть графика функции y = f (x), которая лежит справа от оси Oy. То есть часть графика функции y = f (x), лежащая слева от оси Oy, вообще не ис пользуется в построении графика функции y = f (| x |)). Таким образом,
график функции y = f (| x |) строится так: часть графика функции y = f (x), лежащая справа от оси Oy (и на самой оси), остается без изменений, и эта же часть графика отображается симметрично относительно оси Oy.
Например, на рисунке 23 и в таблице 4 (строка восьмая) с использованием этого правила изображен график функции y = 2| x | – 1.
Рис. 22 |
Рис. 23 |
31
