
4.2. Экстремальные задачи на графовых структурах.
Задачи о раскрасках графов.
Задачи о раскрасках графов.
Задача
о вершинной раскраске.
Каждой вершине
![]() графа поставим в соответствие цвет
графа поставим в соответствие цвет![]() .
.
Определение
4.25.
Вершинная раскраска графа называется
правильной,
если для любого ребра
![]() имеем
имеем![]() .
.
Правильно
раскрашенный граф с некоторой фиксированной
раскраской
![]() обозначим
обозначим![]() ;
;![]() ‑ множество всех правильных раскрасок.
Каждой правильной раскраске поставим
в соответствие число цветов
‑ множество всех правильных раскрасок.
Каждой правильной раскраске поставим
в соответствие число цветов![]() .
.
Определение
4.26.
Хроматическим числом графа
![]() называется величина
называется величина
![]() .
.
Хроматическому
числу ![]() соответствует правильная раскраска
соответствует правильная раскраска
![]() .
.
Немецкий
математик Мёбиус (1790-1868) высказал в 1840
г. предположение, что для плоских графов
![]() ;
это предположение получило название
гипотезы о
четырех красках.
Для плоских графов доказано, что
;
это предположение получило название
гипотезы о
четырех красках.
Для плоских графов доказано, что ![]() 8,
для деревьев
8,
для деревьев ![]() .
Гипотеза о четырех красках в течение
длительного времени оставалась
недоказанной, она стала одной из самых
знаменитых нерешенных задач математики.
В 1976 г. эту гипотезу удалось доказать с
применением компьютера. Было показано,
что если
.
Гипотеза о четырех красках в течение
длительного времени оставалась
недоказанной, она стала одной из самых
знаменитых нерешенных задач математики.
В 1976 г. эту гипотезу удалось доказать с
применением компьютера. Было показано,
что если ![]() для некоторых специальных классов
графов, то это условие выполняется для
всех графов. Если же хотя бы для одного
графа из этих специальных классов
для некоторых специальных классов
графов, то это условие выполняется для
всех графов. Если же хотя бы для одного
графа из этих специальных классов ![]() ,
то гипотеза неверна. Все эти специальные
классы графов были проанализированы
К. Аппелем и В. Хайкеном9
на компьютере, для этого потребовалось
около 2000 ч машинного времени одной из
наиболее мощных ЭВМ того времени;
гипотеза была подтверждена [6].
,
то гипотеза неверна. Все эти специальные
классы графов были проанализированы
К. Аппелем и В. Хайкеном9
на компьютере, для этого потребовалось
около 2000 ч машинного времени одной из
наиболее мощных ЭВМ того времени;
гипотеза была подтверждена [6].
Сформулируем задачу о вершинной раскраске на языке целочисленного линейного программирования.
Пусть
![]() ‑ номер цвета, в который окрашена
вершина
‑ номер цвета, в который окрашена
вершина![]() ,
такая раскраска является правильной,
если, например,
,
такая раскраска является правильной,
если, например,![]() .
Если
.
Если![]() ,
то
,
то![]() ,
что можно записать так:
,
что можно записать так:
![]() или
или
![]() .
.
Целевая функция имеет вид
![]() .
.
Итак, модель описывается соотношениями
![]()
![]() ,
,
![]() ,
,
![]()
Построенная модель нелинейна по ограничениям и целевой функции. Поэтому рассмотрим другую модель. Введем бинарные переменные

Каждая вершина имеет один цвет, что можно записать в виде
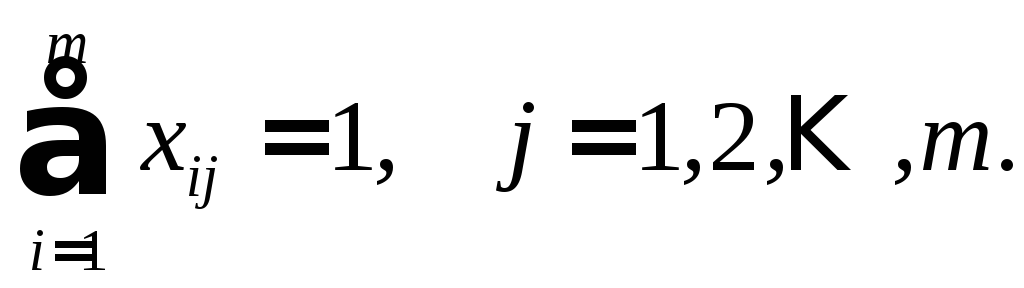
Если
![]() ,
то
,
то
![]()
Если
цвет с номером
![]() входит в раскраску, то
входит в раскраску, то
 ,
,
если
цвет
![]() в раскраску не входит, то
в раскраску не входит, то![]() .
Поэтому модель имеет вид
.
Поэтому модель имеет вид
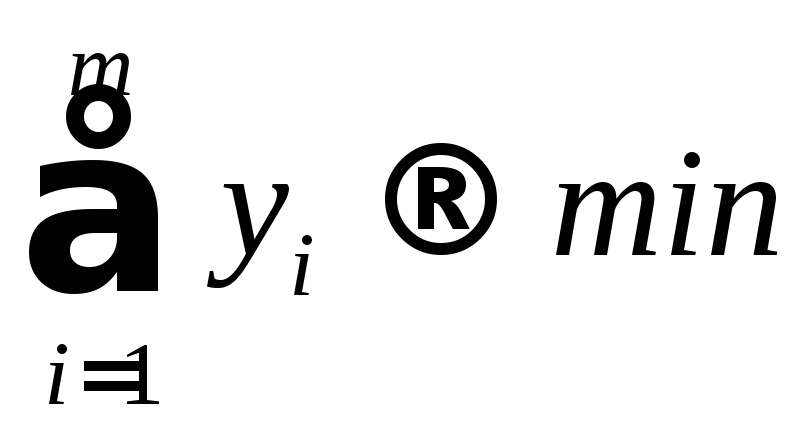 (4.5)
(4.5)
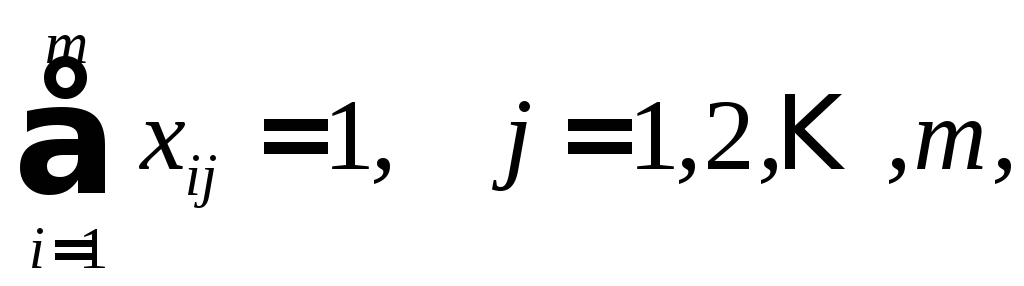 (4.6)
(4.6)
![]() ,
,
![]() . (4.7)
. (4.7)
В
самом деле, если ни одна из двух смежных
вершин
![]() и
и![]() не окрашена в цвет
не окрашена в цвет![]() ,
то
,
то
![]()
если
одна из них (например,
![]() )
окрашена в цвет
)
окрашена в цвет![]() ,
то вторая из них (
,
то вторая из них (![]() )
окрашена в другой цвет, поэтому
)
окрашена в другой цвет, поэтому
![]()
Итак, модель описывается соотношениями (4.5)-(4.7).
Задача о реберной раскраске.
Определение. Реберная раскраска называется правильной, если любые два смежных ребра имеют разные цвета. Реберная раскраска с минимальным числом цветов называется минимальной.
Из этого определения следует, что минимальное число цветов в правильной реберной раскраске оценивается снизу степенью графа, т.е. максимальной степенью вершин.
Минимальное
число цветов
![]() в правильной реберной раскраске
называетсяхроматическим
классом
графа. Пусть
в правильной реберной раскраске
называетсяхроматическим
классом
графа. Пусть
![]()
![]() ‑ степень вершины
‑ степень вершины
![]() .
Для графа без петель и кратных дуг верна
оценка10
.
Для графа без петель и кратных дуг верна
оценка10
![]()
Сформулируем
задачу поиска минимального числа цветов
в реберной раскраске в терминах
целочисленного программирования. Пусть
![]() ‑ номер цвета, в который окрашено
ребро
‑ номер цвета, в который окрашено
ребро
![]() .
.
Тогда модель имеет вид:
![]() (4.8)
(4.8)
![]()
![]() ,
,
![]() ,
,![]() , (4.9)
, (4.9)
![]() (4.10)
(4.10)
4.2.2. Построение остовного дерева минимального веса.
Минимальный остов
Задача
о минимальном остове [6] состоит в
отыскании остова минимального веса во
взвешенном графе
![]() ,
где
,
где![]() ‑ граф,
‑ граф,![]() ‑ вещественнозначная функция, ставящая
в соответствие каждому ребру
‑ вещественнозначная функция, ставящая
в соответствие каждому ребру![]() положительное (или неотрицательное)
число
положительное (или неотрицательное)
число![]() ‑ вес ребра
‑ вес ребра![]() .
.
Задача
о минимальном остове считается одной
из самых «легких» оптимизационных задач
па графах. Решение этой задачи можно
получить с помощью «жадного» алгоритма,
задав процедуру, которая по любому
ациклическому множеству ребер
![]() и ребру
и ребру![]() определяет, содержит ли множество ребер
определяет, содержит ли множество ребер![]() цикл графа
цикл графа![]() .
В качестве такойпроцедуры
можно использовать поиск в глубину,
поскольку выявление цикла в множестве
.
В качестве такойпроцедуры
можно использовать поиск в глубину,
поскольку выявление цикла в множестве
![]() ,
где
,
где![]() ,
равнозначно отысканию
,
равнозначно отысканию![]() -цепи
в порожденном подграфе
-цепи
в порожденном подграфе
![]() .
В процессе работы «жадного» алгоритма
эта процедура выполняется не более
.
В процессе работы «жадного» алгоритма
эта процедура выполняется не более![]() раз, и, следовательно, затраты времени
составят
раз, и, следовательно, затраты времени
составят![]() .
.
Для
упорядочения множества
![]() по неубыванию весов известны алгоритмы
сложности
по неубыванию весов известны алгоритмы
сложности![]() .
Таким образом, даже использование
«жадной» стратегии поиска минимального
остова приводит (независимо от способа
задания графа
.
Таким образом, даже использование
«жадной» стратегии поиска минимального
остова приводит (независимо от способа
задания графа![]() )
к полиномиальному алгоритму сложности
)
к полиномиальному алгоритму сложности
![]() 11.
11.
Рассмотрим
алгоритм построения остовного дерева
минимального веса, предложенный Примом
[2, с. 73]. Алгоритм Прима порождает дерево
посредством разрастания только одного
поддерева, например
![]() ,
содержащего более одной вершины.
«Одиночные» вершины рассматриваются
как отдельные поддеревья (т. е.
,
содержащего более одной вершины.
«Одиночные» вершины рассматриваются
как отдельные поддеревья (т. е.![]() ,
,![]() для всех
для всех![]() ).
Поддерево
).
Поддерево![]() постепенно разрастается за счет
присоединения ребер
постепенно разрастается за счет
присоединения ребер![]() ,
где
,
где![]() и
и ![]() ,
причем добавляемое ребро имеет наименьший
вес
,
причем добавляемое ребро имеет наименьший
вес
![]() среди ребер из
среди ребер из![]() .
Процесс продолжается до тех пор, пока
число ребер в
.
Процесс продолжается до тех пор, пока
число ребер в![]() не станет равным
не станет равным![]() .
Тогда дерево
.
Тогда дерево![]() будет требуемым остовом графа
будет требуемым остовом графа![]() .
.
Алгоритм
начинает работу с присвоения каждой
вершине
![]() пометки
пометки![]() ,
где
,
где![]() на каждом шаге есть ближайшая к
на каждом шаге есть ближайшая к
![]() вершина из
вершина из![]() а
а ![]() ‑ вес ребра
‑ вес ребра
![]() .
На каждом шаге алгоритма вершина,
например
.
На каждом шаге алгоритма вершина,
например![]() ,
с наименьшей пометкой
,
с наименьшей пометкой ![]() присоединяется к
присоединяется к
![]() посредством добавления ребра
посредством добавления ребра![]() .
Поскольку к
.
Поскольку к![]() добавлена новая вершина
добавлена новая вершина ![]() ,
то, может быть, придется изменить пометки
у некоторых вершин
,
то, может быть, придется изменить пометки
у некоторых вершин ![]() ,
и после этого продолжить процесс.
,
и после этого продолжить процесс.
Алгоритм Прима имеет следующий вид.
Инициализация
Пусть
![]() ,
где
,
где ![]() — произвольно выбранная вершина из
— произвольно выбранная вершина из
![]() ,
,![]() .
.
Основной цикл
Шаг
1. Для каждой
вершины ![]() найти вершину
найти вершину ![]() такую, что
такую, что
![]() и приписать вершине
и приписать вершине![]() пометку
пометку
![]() .
Если такой вершины
.
Если такой вершины![]() нет, т. е. при
нет, т. е. при ![]() ,
приписать вершине
,
приписать вершине ![]() пометку
пометку
![]() .
.
Шаг
2. Выбрать
такую вершину ![]() ,
что
,
что
![]() .
.
Обновить данные:
![]() .
.
Если
![]() ,
то останов. Ребра в
,
то останов. Ребра в
![]() образуют остов минимального веса. Если
образуют остов минимального веса. Если![]() ,
то перейти к шагу 3.
,
то перейти к шагу 3.
Шаг
3. Для всех
![]() таких, что
таких, что ![]() обновить пометки следующим образом:
обновить пометки следующим образом:
а)
если ![]() ,
то положить
,
то положить ![]() ,
,
![]() и вернуться к шагу 2;
и вернуться к шагу 2;
б)
если ![]() ,
то перейти к шагу 2.
,
то перейти к шагу 2.
Вычислительная
сложность алгоритма Прима составляет
![]() операций.
операций.
Для решения задачи построения остова минимального веса также используется алгоритм Краскала. Рассмотрим шаги этого алгоритма.
Инициализация
Положить
![]() — несвязный граф, содержащий
— несвязный граф, содержащий![]() вершин.
вершин.
Сортировка
Упорядочить
ребра графа
![]() в порядке неубывания их весов.
в порядке неубывания их весов.
Основной цикл
Шаг
1. Начать с
первого ребра в построенном на шаге
Сортировка
списке. Добавлять ребра графу
![]() ,
соблюдая условие: добавление ребра не
должно приводить к появлению цикла в
,
соблюдая условие: добавление ребра не
должно приводить к появлению цикла в![]() .
.
Шаг
2. Повторять
шаг 1 до тех пор, пока число ребер в
![]() не станет равным
не станет равным![]() .
.
