§ 1.3. Типы интегрирующих и дифференцирующих звеньев и их характеристики

Определение понятия интегрирующих и дифференци­рующих звеньев было дано в общем виде в предыдущем параграфе. Здесь рассмотрим основные их типы.

Идеальное интегрирующее звено. Уравнение и пере­даточная функция звена имеют вид

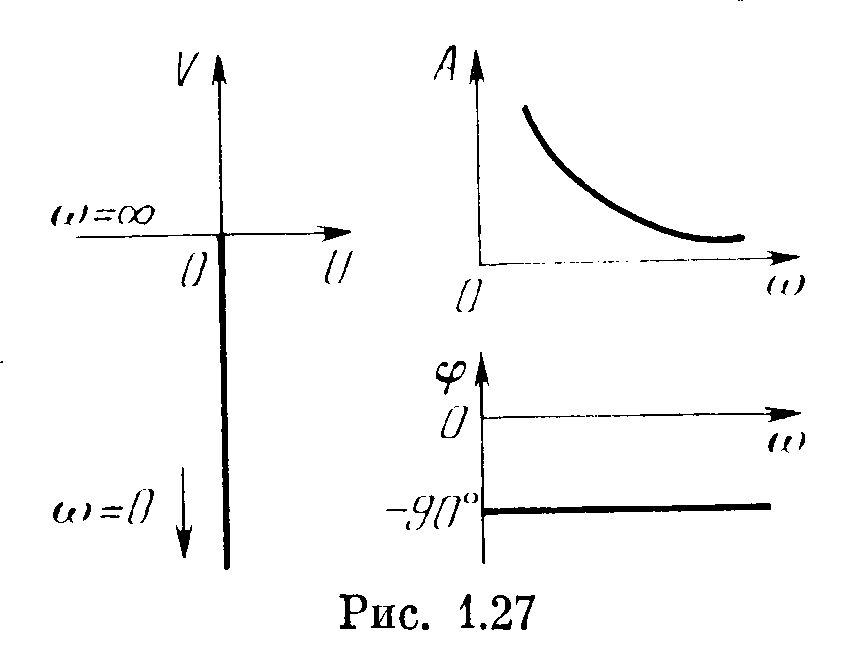
Амплитудно-фазовая частотная характеристика звена (рис. 1.27):

Логарифмическая амплитудная частотная характери­стика

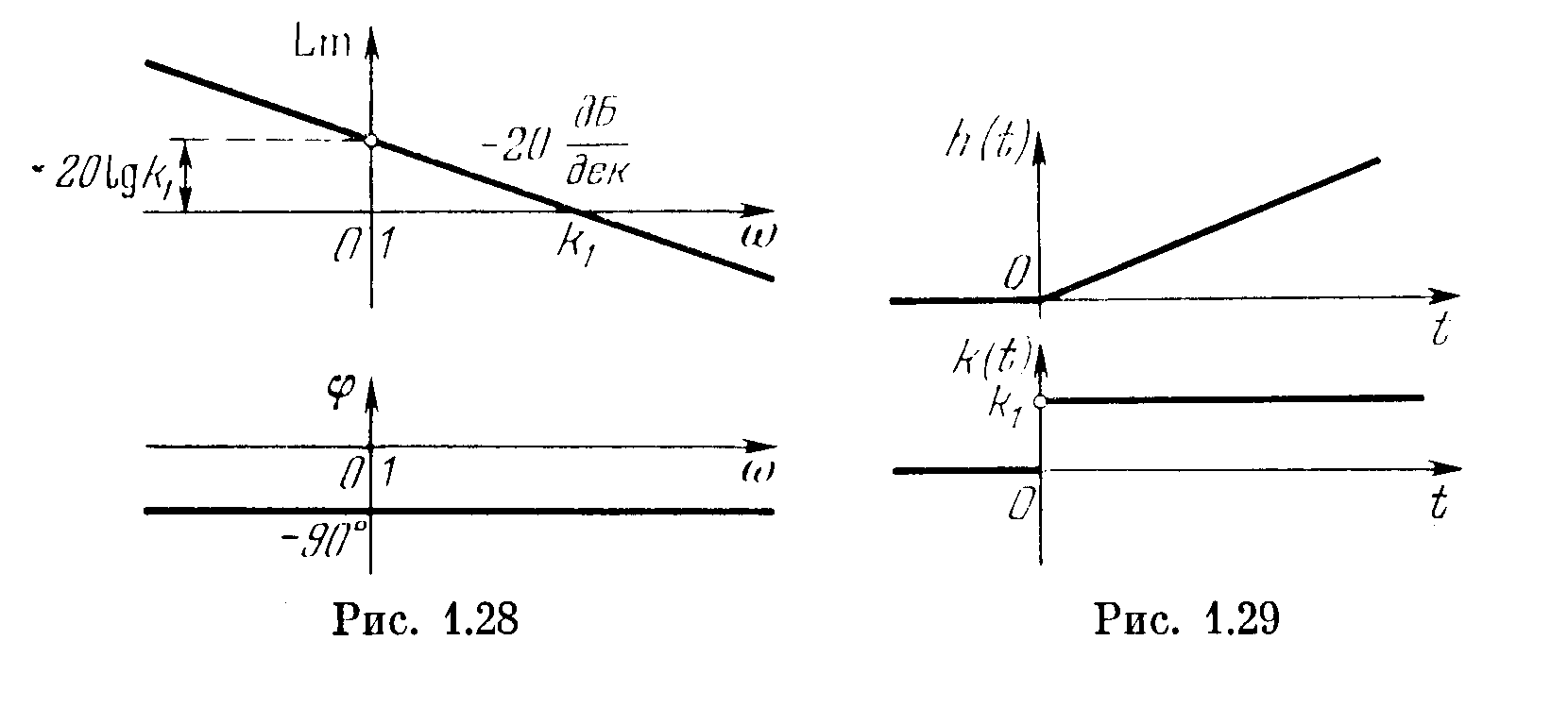
Поскольку на оси абсцисс откладываются значения lg ω, то мы имеем здесь уравнение прямой, проходящей через точку 20 lg k₁ при ω = 1 с наклоном —20 дБ/дек. Это и показано на рис. 1.28 вместе с фазовой частот­ной характеристикой.

Переходная и весовая функция (рис. 1.29) имеют вид

Примеры идеальных интегрирующих звеньев изобра­жены на рис. 1.30.

Инерционное интегрирующее звено. Уравнение и пе­редаточная функция звена

Амплптудно-фазовая частотная характеристика:

Вещественная и мнимая части амплитудно-фазовой характеристики имеют вид

Отсюда видно, что при ω → 0 имеем U→ - k₁T₁ , V → ∞, что и отражено на рис. 1.31.

Логарифмическая амплитудная частотная характе­ристика

Здесь к прежней прямой добавляется наклон —20 дБ/дек,

начиная с частоты , что показано на рис. 1.32.

Там же изображена и логарифмическая фазовая частотная характеристика.

Переходная и весовая функции, как решения уравне­ния звена соответственно при x₁=1(t) и x₁=δ(t), изо­браженные на рис. 1.33, имеют вид

Следовательно, за счет постоянной времени Т₁, вме­сто идеального интегрирования (рис. 1.29), здесь полу­чается интегрирование с инерционным запаздыванием (рис. 1.33).

Примером такого инерционного интегрирующего зве­на является электродвигатель, если выходной величиной считать угол поворота вала двигателя.

Идеальное дифференцирующее звено. Уравнение и передаточная функция звена:

Амплитудно-фазовая частотная характеристика (рис. 1.34) звена:

В реальных системах такой вид характеристики звена возможен лишь в ограниченной полосе частот, так как неограниченное увеличение амплитуды с ростом часто­ты требует бесконечной энергии.

Логарифмические частотные характеристики (рис. 1.35):

В отличие от интегрирующего звена, здесь имеют место положительный наклон +20 дБ/дек и положительная фа­за. Наличие положительной фазы означает опережение сигнала на выходе звена по отношению к входу. Физи­чески это связано с тем, что, как видно из уравнения,

звено реагирует на скорость изменения входной величи­ны, т. е. не на саму величину x₁, а на тенденцию изме­нения ее в будущем. Как говорят, звено обладает пред­сказанием.

Переходная и весовая функции имеют вид

Примерами такого типа звена являются (рис. 1.36) тахогенератор и RС-цепочка с усилителем.

Идеальное звено с введением производной. Уравне­ние и передаточная функция звена:

Амплитудно-фазовая частотная характеристика (рис. 1.37):

Это возможно так же, как и в предыдущем случае, лишь в ограниченной полосе частот. Логарифмические частотные характеристики (рис. 1.38) звена:

Переходная и весовая функции имеют вид

Инерционное дифференцирующее звено. Уравнение и передаточная функция звена:

Амплитудно-фазовая частотная характеристика (рис. 1.39) звена:

Логарифмические частотные характеристики (рис. 1.40):

Переходная и весовая функции (рис. 1.41) имеют вид

Примерами такого типа звена являются (рис. 1.42) обычная цепочка RC, трансформатор, механический демп­фер с пружиной. Здесь мы видим реальное ограничение амплитуды при увеличении частоты (рис. 1.40). Анало­гично и для инерционного звена с введением производ­ной реальное ограничение определяется передаточной функцией

за счет постоянной времени Т₂ .