2.3. Энергия Дзялошинского

Существуют антиферромагнитные кристаллы, в которых магнитные моменты подрешеток упорядочены не точно антипараллельно, а с небольшим скосом. Взаимодействие, противодействующее обмену, вызывающее скос называется энергией Дзялошинского. По природе – это обменнорелятивистское взаимодействие.

Обычно угол скоса не велик, это значит, что энергия Дзялошинского слабее обменного взаимодействия.

2.4. Упругая энергия

Упругая энергия – энергия кристаллической решетки, точнее ее переменной части, связанной с упругими деформациями кристалла.

Явный вид тензора модулей упругости (упругих жесткостей) определяется симметрией кристалла. Здесь мы ограничимся учетом только так называемых акустических типов упругих колебаний решетки. Это не колебания, для которых смещение всех атомов в элементарной ячейке имеют одинаковую фазу (вся элементарная ячейка смещается как одно целое). Фактически это есть обычный звук, для которого характерно то, что частота может быть сколько угодно низкой, обращаясь в ноль при волновом векторе . Другие (так называемые оптические) типы колебаний, минимальная частота которых обычно велика по сравнению с указанными частотами, в большинстве случаев не играют существенной роли в интересующих нас длинноволновых и низкочастотных процессах и могут таким образом не рассматриваться. Указанное обстоятельство проявилось в том, что ни компоненты тензора деформации, ни упругие модулине зависят от номеров подрешеток.

2.5. Магнитоупругая энергия

Взаимная связь между магнитным и упругим состояниями магнетика обусловлена так называемым магнитоупругим (МУ) взаимодействием. Энергию этого взаимодействия можно представить как изменение энергии магнитных (обменных и магнитоанизотропных) взаимодействий, вызванное упругими деформациями. Деформация кристалла ведет к изменению взаимодействия между магнитными моментами атомов, поскольку изменяется расстояние между ними. И наоборот изменение ориентации магнитных моментов деформирует кристалл. МУ взаимодействие относится к разряду сравнительно слабых взаимодействий в магнитных кристаллах. Но в некоторых случаях, МУ взаимодействие может оказаться определяющим для многих свойств магнитоупорядоченных веществ. К исследованию эффектов сильного проявления МУ взаимодействия до сих пор сохраняется не ослабевший интерес. Это относится, в частности, и к динамическому проявлению МУ – к магнитоакустике магнетиков. Впервые большой эффект влияния МУ взаимодействия на динамику магнетика наблюдался в 1963 г. В экспериментах Рудашевского и Шальниковой.

Раздел 3 построение симметрийных инвариантов

3.1.Инварианты упругой энергии

Изменение свободной энергии при изотермическом сжатии кристалла является квадратичной функцией тензора деформации. Эта функция содержит большое число независимых коэффициентов.

. (3.1)

Тензор деформации симметричен: т.е. u_ = u_. Отсюда видно, что произведение u_u_ не меняется при перестановке индексов с, с или пары ,  с парой , . Очевидно, что и модули упругости должны быть определены так, чтобы они обладали такими же свойствами симметрии по отношению к перестановке индексов

. (3.2)

Путем простого подсчета можно убедиться в том, что число различных компонент тензора четвертого ранга, обладающего такими свойствами симметрии равно в общем случае 21 [95].

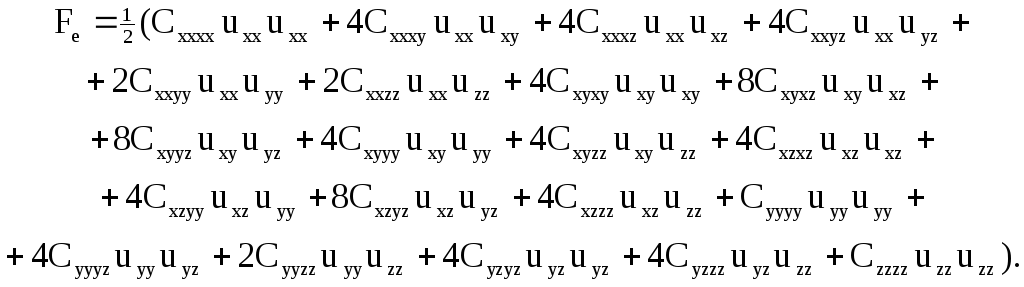(3.3)

Наличие той или иной операции симметрии кристалла приводит к появлению зависимостей между различными компонентами тензора , так что число его независимых компонент оказывается меньшим, чем 21.

Рассмотрим эти соотношения только для ромбоэдрической сингонии, к которой относится борат железа.

Потребуем выполнения уравнений (3.1) по отношению к упругой энергии (3.3).

Ось 2_x эквивалентна преобразованию координат x x, y –y, z –z. Компоненты тензора деформации преобразуются как произведения соответствующих двух координат. Поэтому ясно, что все компоненты с индексами x, y или x, z поменяют свой знак, а остальные останутся неизменными.

Отсюда

(3.4)

Сравнивая формулы (3.3) и (3.4) мы видим, что для соблюдения равенства (3.1) необходимо выполнение следующих условий

С_xxxy = C_xxxz = C_xyyz = C_xyyy = C_xyzz = C_xzyy = C_xzyz = C_xzzz = 0.

Тогда

(3.5)

Теперь рассмотрим действие оператора 3_z на упругую энергию. Для выяснения ограничений, налагаемых на компоненты тензора , удобно произвести формальное преобразование, введя новую систему координат в базисной плоскости x, y. Тогда переход к новой системе координат может быть произведен посредством поворота системы координат на некий угол  (в нашем случае  = 2/3).

, (3.6)

а отсюда

. (3.7)

Тогда для различных наборов тензоров деформации можно записать следующие выражения

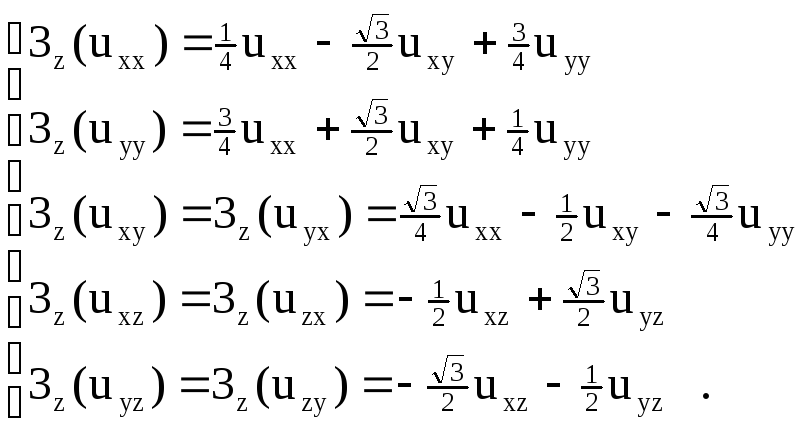(3.8)

Подставим соотношения (3.8) в уравнение (3.5)

(3.9)

Нетрудно видеть, что для выполнения условия (3.1) необходимо положить

(3.10)

(3.11)

(3.12)

Решив системы уравнений (3.10 – 3.12), мы нашли следующие соотношения между модулями упругости:

; ; ; ;

; ; ; ; .

Отсюда может быть получена окончательная формула для упругой энергии

(3.13)

В выражении (3.13) были использованы общепринятые обозначения индексов модулей упругих констант, в соответствии с которыми: ; ; ; ; ; .