2.2. Прямая и плоскость в пространстве

Уравнение плоскости.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

Пусть в пространстве задана ПДСК . Пустьплоскость, точкаи вектор. Тогдауравнение плоскости, проходящей через точку , перпендикулярно вектору имеет вид

. (7)

Общее уравнение плоскости

.

Вектор называется нормальным вектором плоскости.

Уравнение плоскости «в отрезках»

,

где соответственно длины отрезков, отсекаемых плоскостью на координатных осях с точностью до знака.

Уравнение плоскости, проходящей через три точки.

Пусть заданы точки ,,, принадлежащие плоскости. Тогда уравнение плоскостиимеет вид

.

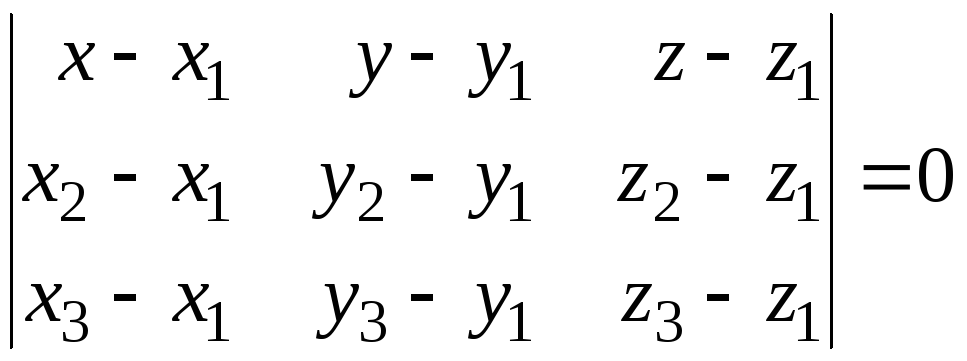Уравнение плоскости, проходящей через точку параллельно двум неколлинеарным векторам.

Пусть плоскость проходит через точку параллельно двум неколлинеарным векторами. Тогда её уравнение

.

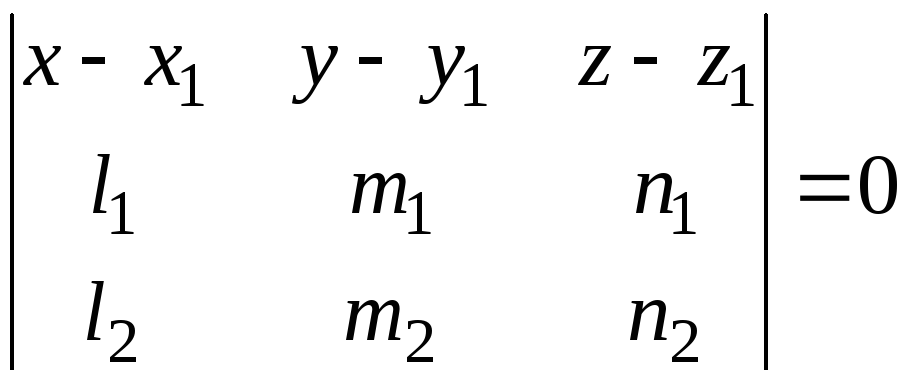Нормальное уравнение плоскости.

Нормальное уравнение плоскости

,

где ,,направляющие косинусы нормали плоскости,расстояние плоскости от начала координат.

Пусть произвольная точка. Расстояние точкиот плоскости вычисляется по формуле:

.

Если задано общее уравнение плоскости , то расстояние точкиот плоскости можно вычислить по формуле

.

Уравнение плоскости, делящей двугранный угол между плоскостями пополам.

Если плоскость делит пополам двугранный угол между плоскостями

, и ,

то уравнение плоскости имеет вид:

.

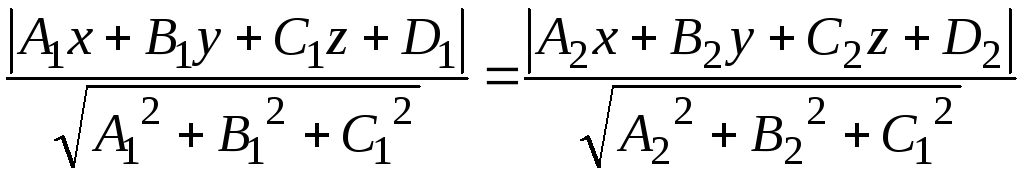Угол между плоскостями

Угол между плоскостями , иравен углу между их нормальными векторами,.а угол между векторами вычисляется по формуле (4). Следовательно,

.

Условие параллельности плоскостей:

.

Условие перпендикулярности плоскостей:

.

Уравнение пучка плоскостей

Пучком плоскостей называется совокупность плоскостей, проходящих через одну прямую.

Если заданы две различные плоскости из пучка (его образующие)

, и ,

то уравнение пучка имеет вид

. (8)

Задача 59. Написать уравнение плоскости, проходящей через точку и перпендикулярной к плоскостями.

Решение. Обозначим нормальный вектор искомой плоскости,инормальные векторы данных плоскостей. По условию задачииСледовательно,

.

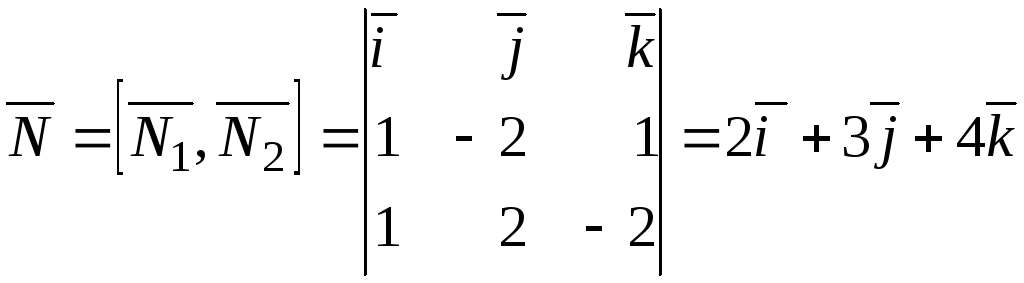Подставим координаты точки m и вектора нормали в уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору (7). Получим

.

Отсюда, уравнение искомой плоскости

.

Задачи для самостоятельного решения

Задача 60. Даны две точки и. Составить уравнение плоскости, проходящей через точкуперпендикулярно вектору.

Задача 61. Найти уравнение плоскости, проходящей через точку параллельно плоскости, если:

1) ,;

2) ,.

Задача 62. Найти уравнение плоскости, проходящей через точку и перпендикулярной к плоскостями, если:

1) ,,;

2) ,,.

Задача 63. Найти уравнение плоскости, проходящей через точки иперпендикулярно к плоскости.

Задача 64. Найти угол между плоскостями:

I) и;

2) и.

Задача 65. Найти уравнение плоскости, которая проходит через точку и отсекает на осях координат равные отрезки.

Задача 66. Найти уравнение плоскости, которая проходит через точку и отсекает на осиотрезок вдвое больший чем на осяхи.

Задача 67. Найти расстояние точки от плоскости.

Задача 68. Найти расстояние точки от плоскости, проходящей через точки,,.

Задача 69. Найти длину перпендикуляра, опущенного из тоски на плоскость.

Задача 70. Найти расстояние между плоскостями:

1) ,;

2) ,.

Задача 71. Написать уравнение плоскости, проходящей через линию пересечения плоскостей ,и

а) через точку ;

б) перпендикулярно к плоскости .

Задача 72. Составить уравнения плоскостей, которые делят пополам двугранные углы, образованные пересекающимися плоскостями:

1) ,;

2) ,.