
- •Глава 1 элементы линейной алгебры
- •1. 1. Определители
- •1) 2)3)4).
- •1.2. Решение систем линейных уравнений с помощью определителей. Формулы Крамера
- •1.3. Матрицы
- •1.4. Решение систем линейных уравнений в матричной форме
- •1); 2);
- •Глава 2 аналитическая геометрия в пространстве
- •2.1. Прямоугольная декартова система координат в пространстве
- •2.2. Простейшие задачи аналитической геометрии в пространстве
- •2.3. Векторная алгебра
- •1) ; 2).
- •2.2. Прямая и плоскость в пространстве
- •2. Уравнения прямой в пространстве
- •Глава 1
- •Глава 2
- •17. ,. 18.. 19.. 20.,. 21.. 23.,,,. 24.,,. 25.,,,,,,. 26.,
1) ; 2).
Задача 35.
Даны точки
![]() ,
,![]() ,
,![]() ,
,![]() .
Проверить, что векторы
.
Проверить, что векторы![]() ,
,![]() коллинеарные, установить какой из них
длиннее и во сколько раз, как они
направлены
коллинеарные, установить какой из них
длиннее и во сколько раз, как они
направлены![]() в
одну или в противоположные стороны.
в
одну или в противоположные стороны.
Задача 36.
Найти единичный вектор
![]() ,
параллельный вектору
,
параллельный вектору![]() .
.
Скалярное произведение
Скалярным
произведением двух
ненулевых векторов
![]() и
и![]() называется число, равное произведению
длин этих векторов на косинус угла между
ними. Если хотя бы один из векторов
нулевой, то скалярное произведение, по
определению, полагается равным нулю.
Обозначается
называется число, равное произведению
длин этих векторов на косинус угла между
ними. Если хотя бы один из векторов
нулевой, то скалярное произведение, по
определению, полагается равным нулю.
Обозначается![]() или
или![]() .
.
Из определения
![]() .
.
Так как
![]() ,
,![]() ,
то
,
то
![]() .
.
![]() Свойства
скалярного произведения
Свойства
скалярного произведения
 .
. .
. .
. .
.Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда векторы перпендикулярны (ортогональны).
![]() Скалярное
произведение в ПДСК
Скалярное
произведение в ПДСК
Если известны
координаты двух векторов в ПДСК
![]() и
и![]() ,
то
,
то
![]() .
(7)
.
(7)
Отсюда следует необходимое и достаточное условие ортогональности векторов:
![]() .
.
Угол между векторами
![]() и
и![]() вычисляется по формуле
вычисляется по формуле
 .
(8)
.
(8)
Задача 37.
Определить углы треугольника
![]() с вершинами
с вершинами![]() ,
,![]() ,
,![]() .
.
Решение.
Определим угол при вершине
![]() .
Он образован векторами
.
Он образован векторами![]() и
и![]() (Рис.7).
(Рис.7).
П о
формуле (8)
о
формуле (8)
![]() .
.
Найдём координаты указанных векторов по формуле (5). Получим
![]() ,
,
![]() .
.
Вычислим длины
векторов![]() и
и![]() ,
используя формулу (6):
,
используя формулу (6):
![]() ,
,
![]() .
.
Вычислим скалярное
произведение векторов
![]() ,
используя формулу (7)
,
используя формулу (7)
![]() .
.
Так как скалярное
произведение равно нулю, то векторы
![]() и
и![]() ортогональны и треугольник прямоугольный.
Следовательно,
ортогональны и треугольник прямоугольный.
Следовательно,
![]() .
Так как
.
Так как
![]() ,
то треугольник равнобедренный. Значит,
,
то треугольник равнобедренный. Значит,![]() .
.
Задачи для самостоятельного решения
Задача 38.
Вычислить
![]() ,
если:
,
если:
1)
![]() и
и![]() ;
;
2)
![]() и
и![]() .
.
Задача 39.
Определить при каком значении
![]() векторы
векторы![]() и
и![]() ортогональны, если:
ортогональны, если:
1)
![]() и
и![]() ;
;
2)
![]() и
и![]() .
.
Задача 40.
Вычислить косинус угла, образованного
векторами
![]() и
и![]() ,
если:
,
если:
1)
![]() и
и![]() ;
;
2)
![]() и
и![]() .
.
Задача 41.
Найти
![]() и
и![]() ,
если:
,
если:
1)
![]() и
и![]() ;
;
2)
![]() и
и![]() .
.
Задача 42.
Даны вершины треугольника
![]() .
Определить угол при вершине
.
Определить угол при вершине![]() если:
если:
1)
![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() .
.
Векторное произведение.
Пусть задана тройка
векторов
![]() .
Будем называть еёупорядоченной,
если указано, какой из векторов считать
первым, какой вторым, какой третьим.
.
Будем называть еёупорядоченной,
если указано, какой из векторов считать
первым, какой вторым, какой третьим.
Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу, из конца третьего вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка левая.
Векторным
произведением вектора
![]() на вектор
на вектор
![]() называется вектор
называется вектор![]() ,
удовлетворяющий следующими трём
условиям:
,
удовлетворяющий следующими трём
условиям:
1)
![]() ,
где
,
где![]() угол
между векторами
угол
между векторами![]() и
и![]() ;
;
2)
![]() и
и![]() ;
;
3) векторы
![]() образуют правую тройку.
образуют правую тройку.
Обозначается векторное произведение
![]()
Свойства векторного произведения
1. Векторное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда векторы коллинеарны.
2. Модуль векторного произведения векторов равен площади параллелограмма, построенного на этих векторах:
![]() .
(9)
.
(9)
3.
![]() .
.
4.
![]() .
.
5.
![]()
Векторное произведение в ПДСК
Если векторы
![]() и
и![]() ,
то векторное произведение вычисляется
по формуле:
,
то векторное произведение вычисляется
по формуле:
 .
(10)
.
(10)
Задача 43.
Вычислить площадь треугольника
![]() ,
если
,
если![]() ,
,![]() ,
,![]() и найти длину высоты треугольника
и найти длину высоты треугольника![]() ,
которая опущена из вершины
,
которая опущена из вершины![]() .
.
Решение.
Найдём координаты векторов
![]() ,
,![]() и
и![]() (см. (5)):
(см. (5)):
![]() ,
,
![]() ,
,![]()
Площадь треугольника
![]() равна половине площади параллелограмма,
построенного на векторах
равна половине площади параллелограмма,
построенного на векторах![]() и
и![]() .
Найдём площадь параллелограмма по
формуле (9). Для этого вычислим векторное
произведение этих векторов, используя
формулу (10):
.
Найдём площадь параллелограмма по
формуле (9). Для этого вычислим векторное
произведение этих векторов, используя
формулу (10):
 .
.
Следовательно,
![]() .
.
Из школьного курса
геометрии известно, что,
![]() ,
где
,
где![]() высота треугольника,
высота треугольника,![]() длина стороны, на которую опущена высота.
Следовательно,
длина стороны, на которую опущена высота.
Следовательно,
![]() .
.
Тогда
![]() .
.
Задачи для самостоятельного решения
Задача 44. Упростить:
1)
![]() ;
;
2)
![]() ;
;
3).
![]() .
.
Задача 45.
Найти векторное произведение
![]() ,
если:
,
если:
1)
![]() и
и![]() ;
;
2)
![]() и
и![]() .
.
Задача 46.
Вычислить площадь параллелограмма,
построенного на векторах
![]() и
и![]() ,
если:
,
если:
1)
![]() и
и![]() ;
;
2)
![]() и
и![]() .
.
Задача 47.
Вычислить площадь треугольника
![]() ,
если:
,
если:
1)
![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() .
.
Задача 48.
Даны вершины треугольника
![]() .
Найти длину его высоты, которая опущена
из вершины
.
Найти длину его высоты, которая опущена
из вершины![]() если:
если:
1)
![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() .
.
Задача 49*
. Вектор
![]() ,
ортогональный к векторам
,
ортогональный к векторам![]() и
и![]() ,
образует с осью
,
образует с осью![]() тупой угол. Зная, что
тупой угол. Зная, что![]() ,
найти его координаты.
,
найти его координаты.
Задача 50*
. Вектор
![]() ,
перпендикулярный к оси
,
перпендикулярный к оси![]() и к вектору
и к вектору![]() ,
образует с осью
,
образует с осью![]() острый угол. Зная, что
острый угол. Зная, что![]() ,
найти его координаты.
,
найти его координаты.
Задача 51*.Найти
вектор
![]() ,
зная, что он перпендикулярен к векторам
,
зная, что он перпендикулярен к векторам![]() и
и![]() и удовлетворяет условию
и удовлетворяет условию![]()
Смешанное произведение трёх векторов.
Смешанным
произведением
трёх векторов называется произведение
вида
![]() ,
где векторное произведение первых двух
векторов умножается скалярно на третий
вектор. Обозначается
,
где векторное произведение первых двух
векторов умножается скалярно на третий
вектор. Обозначается
![]() .
.
Смешанное
произведение
![]() равно объёму параллелепипеда, построенного
на векторах
равно объёму параллелепипеда, построенного
на векторах![]() ,
взятому со знаком «+», если тройка правая,
со знаком «
,
взятому со знаком «+», если тройка правая,
со знаком «![]() »
если тройка левая.
»
если тройка левая.
Если векторы
![]() компланарные, то
компланарные, то![]() .
.
![]() Смешанное
произведение в ПДСК
Смешанное
произведение в ПДСК
Если известны
координаты векторов
![]() ,
,![]() ,
,![]() ,
то смешанное произведение вычисляется
по формуле
,
то смешанное произведение вычисляется
по формуле
 .
.
Объём параллелепипеда,
построенного на векторах
![]() равен
равен
 .
.
Объём треугольной
пирамиды, построенной на векторах
![]() равен
равен
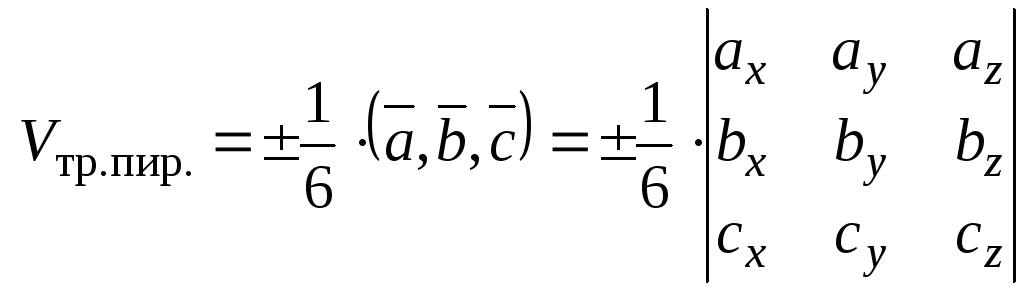 .
.
Задача 52.
Даны вершины треугольной пирамиды
![]() ,
,![]() ,
,![]() ,
,![]() .
Найти длину её высоты
.
Найти длину её высоты![]() ,
которая опущена на грань
,
которая опущена на грань![]() (Рис. 8).
(Рис. 8).
Р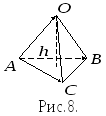 ешение.
Рассмотрим векторы
ешение.
Рассмотрим векторы
![]() ,
,![]() ,
,![]() ,
на которых построена треугольная
пирамида
,
на которых построена треугольная
пирамида![]() .
Найдём их координаты:
.
Найдём их координаты:
![]() ,
,
![]() ,
,![]() .
.
Из школьного курса геометрии известна формула объёма пирамиды:
![]() .
.
В основании лежит
треугольник
![]() ,
его площадь
,
его площадь
![]() .
.
Следовательно,
![]() .
.
С другой стороны,
![]() .
.
Тогда
![]() .
.
Вычислим смешанное произведение:
 .
.
Вычислим векторное произведение:
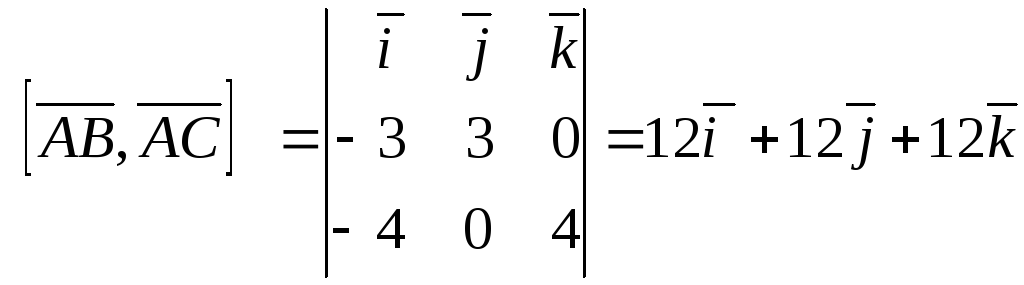 .
.
Далее, найдём модуль этого векторного произведения:
![]() .
.
Тогда высота пирамиды
![]() .
.
Задачи для самостоятельного решения
Задача 53.
Вычислить
![]() ,
если
,
если
1)
![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() .
.
Задача 54.
Установить, компланарны ли векторы
![]() ,
если:
,
если:
1)
![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() .
.
Задача 55.
Доказать, что точки
![]() лежат в одной плоскости, если:
лежат в одной плоскости, если:
1)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Задача 56.
Вычислить объём пирамиды
![]() ,
если:
,
если:
1)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Задача 57.
Найти длину высоты пирамиды
![]() ,
которая опущена на грань
,
которая опущена на грань![]() ,
если:
,
если:
1)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Задача 58.
Объём тетраэдра
![]() .
Три его вершины находятся в точках
.
Три его вершины находятся в точках![]() ,
,![]() ,
,![]() .
Найти координаты четвертой вершины
.
Найти координаты четвертой вершины![]() ,
если известно, что она лежит на оси
,
если известно, что она лежит на оси![]() .
.
