2.2. Простейшие задачи аналитической геометрии в пространстве

Расстояние между двумя точками.

Пусть заданы две точки и. Расстояние между ними находится по формуле:

.

Деление отрезка в заданном отношении.

Даны две точки и. Пусть точкаделит отрезокв заданном отношении.тогда её координаты находятся по формулам:

, ,.

В частности, при получим координаты середины отрезка:

, ,.

Задачи для самостоятельного решения

Задача 16. Доказать, что треугольник с вершинами ,,равнобедренный.

Задача 17. На оси абсцисс найти точку, расстояние которой от точки равно 12.

Задача 18. На оси ординат найти точку, равноудалённую от точек и.

Задача 19. Даны вершины треугольника ,,вычислить длину его медианы, проведённой из вершины.

Задача 20. Даны три вершины ,,параллелограмма. Найти его четвёртую вершину.

Задача 21. Даны вершины треугольника ,,. Вычислить длину биссектрисы его внутреннего угла при вершине.

2.3. Векторная алгебра

Понятие вектора

Отрезок прямой, для концов которого установлен порядок (т. е. указана начальная и конечная точки) называется направленным отрезком.

Направленный отрезок называется вектором.

Вектор с началом и концомбудем обозначатьили просто.

Вектор, у которого начало и конец совпадают, называется нулевым вектором или вектором.

Длина направленного отрезка называетсямодулем вектора и обозначается.

Вектор, имеющий модуль равный 1, называется единичным.

Единичный вектор, имеющий одинаковое направление с данным вектором , называетсяортом вектора и обозначается.

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Два вектора называются равными, если они коллинеарны, одинаково направлены и их длины равны.

Два вектора называются противоположными, если они коллинеарны, противоположно направлены и их длины равны.

Векторы, лежащие на одной плоскости или на параллельных плоскостях, называются компланарными.

Линейные операции над векторами

Сложение векторов

Суммой двух векторов иназывается третий вектор, начало которого совпадает с началом вектора, а конецс концом векторапри условии, что векторприложен к концу вектора(правило треугольника) (Рис. 2). Тогда

Н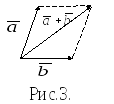аряду с правилом треугольника часто пользуются равносильным ему правилом параллелограмма: если векторыиприведены к общему началу и на них построен параллелограмм, то суммаесть вектор, совпадающий с диагональю этого параллелограмма, идущий из общего начала векторови(Рис.3).

Сложение векторов подчиняется основным законам сложения чисел:

, .

Эти свойства позволяют определить сумму любого числа слагаемых по правилу замыкающего вектора, при этом слагаемые можно перемещать и группировать произвольным образам.

Разностью векторов иназывается третий вектор, который в сумме с векторомдаёт вектор.

Если два вектора приведены к общему началу, то их разность есть вектор, идущий из конца «вычитаемого» к началу «уменьшаемого» вектора (Рис. 4).

Умножение вектора на число

Произведением вектора и числа называется вектор , который коллинеарен вектору , имеет длину равную , сонаправлен с вектором , если , и противоположнонапровлен, если. Еслиили , то . Обозначается

Геометрический смысл операции умножения вектора на число можно выразить следующим образом: если , то вектор «растягивается» в раз, если, то «сжимается» враз. Принаправление не меняется, принаправление меняется на противоположное.

Из определения следует, что ,вектор противоположный вектору. Обозначим его.

Проекция вектора на ось

Пусть задан вектори оськоторая определяется вектором. Обозначимипроекции точекина ось (Рис. 5).

Тогда проекцией вектора на осьназывается длина отрезкавзятая со знаком «», если вектор имеет направление оси, и со знаком «» в противном случае. Обозначается

.

Пусть вектор составляет уголс положительным направлением оси. Тогда

.

Свойства проекций:

1. Равные векторы имеют равные проекции.

2. .

3. .

Координаты вектора

Пусть в пространстве задана ПДСК и произвольный вектор. Пусть, далее,,,. Проекции,,векторана оси координат называются егокоординатами. При этом пишут

.

Если заданы координаты точек и, то координаты вектора

. (5)

Следовательно, модуль вектора

. (6)

Пусть единичные векторы осей координат. Тройка векторовназываетсябазисом.

Каким бы ни был вектор он всегда может быть разложен по базису векторов, т.е. может быть представлен в виде:

.

Коэффициенты этого разложения являются координатами вектора . Еслии, то

,

.

Два вектора коллинеарны тогда и только тогда когда их координаты пропорциональны:

.

Направляющие косинусы

Еслиуглы, образованные векторомс положительными направлениями осей координат (Рис. 6), то,,называютсянаправляющими косинусами вектора .

Если , то

, ,

Отсюда имеем

, ..

Имеет место равенство:

.

Задачи для самостоятельного решения

Задача 22. По данным векторам ипостроить следующие векторы:

1) ; 2); 3); 4); 5); 6); 7); 8).

Задача 23. В параллелограмме обозначены,. Выразить черезивекторы,,,, гдеточка пересечения диагоналей параллелограмма.

Задача 24. В треугольнике обозначены:,. Выразить черезивекторы, совпадающие с медианами треугольника,,.

Задача 25. В правильном шестиугольнике обозначены:,. Выразить черезивекторы,,,,,,.

Задача 26. В ромбе даны диагонали,. Выразить черезивекторы, совпадающие со сторонами ромба:,,,.

Задача 27. Даны точки и. Найти координаты векторови.

Задача 28. Дан вектор . Найти координаты точки, если известны координаты точки.

Задача 29. Определить начало вектора , если его конец совпадает с точкой.

Задача 30. Найти вектор , зная две его координаты,и модуль.

Задача 31. Вычислить направляющие косинусы вектора .

Задача 32. Даны точки и. Найти длину и направление вектора.

Задача 33. Определить при каких значениях ивекторы,коллинеарные.

Задача 34. Найти орт вектора , если: