1); 2);

3); 4);

5) .

Задача 11. Найти обратную матрицу:

1) 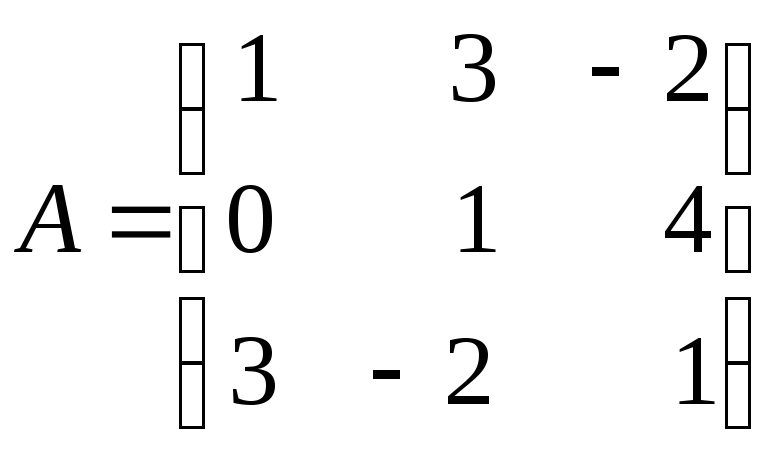; 2).

Задача 12. Решить систему уравнений матричным способом:

1) 2) 3)

1.5. Метод Гаусса

Решение систем линейных уравнений с помощью определителей удобно производить для систем двух или трёх уравнений. В случае же систем большего числа уравнений удобнее пользоваться методом Гаусса, который заключается в последовательном исключении неизвестных.

Пусть задана система линейных уравнений снеизвестными:

Обозначим матрицу системы,расширенную матрицу системы:

, .

Умножение какого-либо уравнения системы на число и прибавление к другому уравнению не меняет системы. Используя этот факт, преобразуем расширенную матрицу системы к следующему виду: в первом столбце все элементы, начиная со второго равны нулю; во втором столбце все элементы, начиная с третьего равны нулю; в третьем— начиная с четвёртого и т.д. В результате матрица приводится к ступенчатому виду.

Возможны три основные случая:

1)

Матрица имеет треугольный вид (число неизвестных равно числу линейно независимых уравнений), система имеет единственное решение. Записываем систему, соответствующую преобразованной матрице, из последнего уравнения находим , подставляем в предпоследнее уравнение и находим, затеми т. д.

2) .

Система содержит хотя бы одно уравнение вида , система не имеет решений.

3) .

Матрица не треугольная, так как последнее уравнение содержит более одного неизвестного, система имеет бесконечно много решений.

Задача 13. Решить систему методом Гаусса

Решение. Выпишем расширенную матрицу системы и преобразуем её:

1) поменяем местами первую и вторую строки:

;

2) прибавим ко второй строке первую, умноженную на , а к третьейпервую, умноженную на:

;

3) прибавим к третьей строке вторую, умноженную на :

.

Система уравнений приняла треугольный вид:

Она имеет единственное решение. Из последнего уравнения , подставляя это значение во второе уравнения, получаем. Из первого уравнения находим.

Задача 14. Решить систему методом Гаусса

Решение. Выпишем расширенную матрицу системы и преобразуем её:

.

1) Прибавим ко второй строке первую, умноженную на , а к третьейпервую, умноженную на, получим

.

2) Прибавим к третьей строке вторую, умноженную на :

.

Матрица приведена к ступенчатому виду, и последнее уравнение содержит несколько неизвестных. Следовательно, система имеет бесконечно много решений.

Первое и второе уравнение преобразованной системы и перепишем в виде:

Выразим неизвестные ичерези:

, .

Придавая иразличные числовые значения, будем получать различные решения данной системы.

Задачи для самостоятельного решения

Задача 15. Решить следующие системы методом Гаусса.

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)
11)	12)

Глава 2 аналитическая геометрия в пространстве

2.1. Прямоугольная декартова система координат в пространстве

Прямоугольная декартовая система координат в пространстве представляет собой три взаимно перпендикулярные пересекающиеся в одной точке координатные оси,,, имеющие одинаковый единичный отрезок.

Точканачало координат,ось абсцисс,ось ординат,ось аппликат (рис. 1). Тогда каждой точкепространства можно поставить в соответствие упорядоченную тройку действительных чисел, которые называюткоординатами точки.

Плоскости ,,называютсякоординатными плоскостями. Они разбивают пространство на 8 октантов. Точка , точки на осиимеют координаты, на оси, на оси, на плоскости, на плоскости, на плоскости.