3.2.5. Планетарные редукторы

Цель - изучение конструктивных особенностей и принципа работы планетарной передачи, выяснение ее достоинств, недостатков и области применения, умение выполнять основные геометрические, силовые и прочностные расчеты.

Простыми планетарными передачами называют такие, которые содержат зубчатые колеса с перемещающимися осями (рис. 3.23). Перемещающиеся зубчатые колеса называют планетарными или сателлитами (q), они вращаются вокруг своих осей и вместе с осью вокруг центрального неподвижного колеса (a). Оси сателлитов расположены во вращающемся звене, называемом водилом (h), неподвижное зуб­чатое колесо (b) является корпусом.

Если сделать подвижными все зубчатые колеса и водило, то такая передача называется дифференциальной или дифференциалом ( рис.3.24 ).

Рис. 3.23. Простая плане- Рис. 3.24.Дифференциаль-

тарная передача ная планетарная передача

Планетарные передачи могут использоваться в качестве редукторов с постоянным передаточным отношением, илив качестве коробки скоростей, передаточное отношение в которой изменяют путем торможения различных звеньев, или в качестве дифференциального механизма. К достоинствам планетарных пере­дач относятся также возможность получения значительных пе­редаточных отношений, компактность и небольшой вес, малые нагрузки на опоры вследствие симметричности расположения сателлитов и взаимного уравновешивания сил. К недостаткам планетарных передач можно отнести повышенные требования к точности изготовления, сложность сборки и регулировки. Планетарные передачи находят применение на автомобильном транспорте.

Поскольку кинематика планетарных передач подробно рассматривается в курсе "Теория механизмов и машин", то формулу для определения передаточного отношения для схемы, представленной на рис. 3.24, запишем в окончательном виде:

,

где _вх, _вых - угловые скорости на входе и выходе,

n₁, n₂ - частота вращения входного и выходного валов.

При последовательном соединении нескольких планетарных передач передаточное отношение определится как произведение передаточных отношений отдельных ступеней. Например, для двух последовательно соединенных передач (рис. 3.25) имеем

где z_a1, z_a2, z_b1, z_b2 - числа зубьев колес.

У планетарных передач КПД равен  = 0,96 ... 0,98 для значений i  15. С увеличением передаточного отношения рабо­та планетарной передачи ухудшается, возрастают потери и КПД получается низким. В этом случае предпочтение следует отдавать многоступенча­тым передачам. Находят применение одноступенчатые передачи с величиной i = 30…100, но значение КПД при этом составляет  = 0,8…0,65.

Расчет на прочность зубьев планетарных передач выполняют по формулам для зубчатых передач. Поскольку зубья колес при внутреннем зацеплении являются более прочными чем зубья внешнего зацепления, то при одинаковых свойствах материалов колес можно рассчитать только внешнее зацепление. Последовательность расчета цилиндрических зубчатых колес изложена в разделах 3.2.2., 3.2.3.

Особенности расчета планетарных передач рассмотрены ниже. Так коэффициенты долговечности К_HL и К_FL находят по эквивалентному числу циклов перемены напряжений зубьев при вращении колес только относительно друг друга. Для центральной шестерни имеем N_экв=573 C₁^/ L_h ,

для сателлитов N_экв= 573 C₂^/ L_h

где ₁^{/ =} ₁ - _h , ₂^{/ =} ₁^{/ -} Z₁ / Z₂ .

Межосевое расстояние для прямозубой передачи определить по формуле и согласовать с ГОСТом. ,

где u^/ = Z₂ / Z₁ ^, К_с = 1,1…1,2 - неравномерность распределения нагрузки между сателлитами,

Т₁- момент на центральной шестерни, Н.мм,

= 0,5 – 0,4 – коэффициент ширины венца колеса.

Ширина колеса на корпусе - b = .

Делительный диаметр ведущей шестерни равен

d₁ = 2/u^/ + 1.

Модуль зацепления равен m = d₁ / Z₁.

Значение модуля округляют до стандартной величины и уточняют следующие параметры:

Z₁ = 2/m (u^/ + 1), Z₂ = Z₁ u^/, Z₃ =Z₁ + 2 Z₂ .

Числа зубьев колес определяют исходя из заданного передаточного отношения и требуемых габаритов. При известном передаточном отношении задаются числом зубьев ведущей шестерни и определяют числа зубьев остальных колес по приведенным выше соотношениям.

Полученные значения корректируют с учетом следующих требований:

из условия соосности, по которому межосевые расстояния зубчатых пар с внешним и внутренним зацеплениями должны быть раны -

z_q = 0,5 (z_b – z_a);

из условия собираемости, которое требует, чтобы в зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами для обеспечения возможности сборки передачи. Условие имеет следующий вид:

из условия соседства, по которому требуется, чтобы сателлиты при вращении не задевали поверхностями зубьев друг друга. Для этого необходимо, чтобы сумма радиусов вершин зубьев соседних сателлитов была меньше расстояния между их осями, т.е соблюдалось неравенство z_q + 2 < (z_a + z_q) sin  /c, где с - число сателлитов.

При необходимости проводят корректировку найденных чисел зубьев для обеспечения выполнения указанных выше условий.

Усилия в планетарных передачах можно определить в соответствии с рис. 3.26. Из условия равновесия сателлита получают следующие соотношения:

Здесь F_ta, F_tb, F_th - окружные усилия на соответствующих колесах и водиле;

T₁ - крутящий момент, передаваемый шестерней I;

d_w1 - начальный диаметр шестерни;

c - число сателлитов;

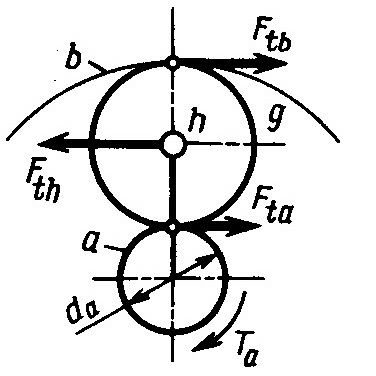
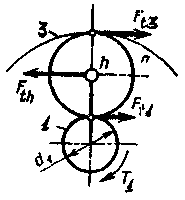
Рис. 3.25 Двухступенчатый Рис. 3.26. Усилия в

планетарный редуктор планетарной передаче

Нагрузки на зубья колес уменьшаются пропорционально количеству сателлитов. При симметричном расположении сателлитов входные и выходные валы нагружены только крутящим моментом, а опоры разгружены от радиальных нагрузок.

Поскольку нагрузки на зубья уменьшаются пропорционально числу сателлитов, то в формулы для напряжений вводят сомножитель .

Расчет зубьев планетарных передач на изгибную и контактную выносливость выполняют по формулам для цилиндрических колес. При этих расчетах должны выполняться условия . Допускаемые напряжения определяют с учетом заданного графика работы механизма

Смазка зубчатых колёс планетарной передачи проводится путем погружения сателлитов в масляную ванну. Однако при больших скоростях вращения вход сателлитов в масляную ванну сопровождается значительными гидравлическими потерями. В этом случае используют смазку разбрызгиванием или струйным поли­вом.

Контрольные вопросы

1. Какая зубчатая передача называется планетарной, принцип ее работы , назначение и устройство ?

2. В каком случае планетарная передача называется дифференциалом ?

3. Каковы преимущества и недостатки планетарных передач ?

4. Какой принцип применяют при выводе формулы для определения передаточного

отношения планетарной передачи ?

5. В чем заключаются условия соосности, сборки и соседства планетарных передач ?