
- •1.Определение функции. Способы и задание функции. Предел функции стремящимся к x0 и плюс минус бесконечности
- •2. Односторонние пределы .
- •4. Первый классический предел
- •6. Бесконечно малая функция
- •7.Сравнение бесконечно малых функций
- •8. Определение непрерывности функции Точки разрыва
- •13.Определение и геометрический смысл дифференциалов
- •14.Приближённое вычисление с помощью дифференциалов
- •16. Понятие дифференцируемости функции данной точки . Связь между понятие дифференцированности и непрерывности
- •17.Теорема Ферма
- •18.Теорема Ролля
- •19. Теорема Лагранжа
- •21. Правила лопиталя
- •22. Признаки монотонности функции
- •23.Достаточные условия локального экстремума
- •24. Необходимое условие локального экстремума Необходимые условия существования локальных экстремумов[править]
- •25. Направление выпуклости и вогнутости графиков функции 26. Точка перегиба графика функции. Необходимое и достаточное условие точки перегиба 27. Асимптоты графика функции
- •28. Понятие первообразной неопределенной функции 29. Основные свойства неопределенного интеграла
- •30. Интегрирование методом замены переменной
- •31. Интегрирование неопределенного интеграла по частям
- •32. Интегрированы рациональной функции
- •33. Интегрирование геометрической функции
14.Приближённое вычисление с помощью дифференциалов
Приближённые вычисления с помощью дифференциала
Формулу
![]()
задающую определение дифференциала, можно записать в виде приближённого равенства
![]()
если
считать (при малых
![]() )
значение бесконечно малой величины
)
значение бесконечно малой величины![]() много
меньшим, чем
много
меньшим, чем![]() .
Перенося
.
Перенося![]() в
правую часть, получаем:
в
правую часть, получаем:
![]()
где
![]() .
С учётом выражения дифференциала через
частные производные, находим, что
.
С учётом выражения дифференциала через
частные производные, находим, что
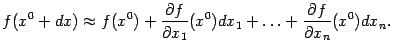
Эту
формулу можно применять для приближённого
вычисления значений функции
![]() в
точках
в
точках![]() ,
если известны значения
,
если известны значения![]() и
её частных производных
и
её частных производных![]() в
точке
в
точке![]() .
15.Производные
и дифференциалы высших порядков
.
15.Производные
и дифференциалы высших порядков
Производные и дифференциалы высших порядков
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,
f"(x) = (f'(x))'.
Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x).
Число n называется порядком производной.
Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N.
Если x - независимая переменная, то
dx = const и d2x = d3x = ... = dnx = 0.
В этом случае справедлива формула
dnf(x) = f(n)(x)(dx)n.
16. Понятие дифференцируемости функции данной точки . Связь между понятие дифференцированности и непрерывности
17.Теорема Ферма

18.Теорема Ролля
19. Теорема Лагранжа
Теорема. Пусть функция дифференцируема в открытом промежутке и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка , что (13)
![]()
Доказательство. Рассмотрим вспомогательную функцию

Эта функция непрерывна и дифференцируема в промежутке , а на его концах принимает одинаковые значения:
![]()
Тогда удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка , в которой производная функции равна нулю:
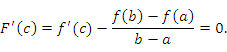
Следствие
1. В частном случае, когда
![]() , из теоремы Лагранжа вытекает, что
существует точка
, из теоремы Лагранжа вытекает, что
существует точка![]() ,
в которой производная функции
,
в которой производная функции![]() равна нулю:
равна нулю:![]() . Это означает, что теорема Лагранжа
является обобщением теоремы Ролля.
. Это означает, что теорема Лагранжа
является обобщением теоремы Ролля.
Следствие
2. Если
![]() во всех точках некоторого промежутка
во всех точках некоторого промежутка![]() , то
, то![]() в этом промежутке.
в этом промежутке.
Действительно,
пусть
![]() и
и![]() – произвольные точки промежутка
– произвольные точки промежутка![]() и
и![]() . Применяя теорему Лагранжа к промежутку
. Применяя теорему Лагранжа к промежутку![]() , получим
, получим
![]()
Однако
![]() во всех точках промежутка
во всех точках промежутка![]() . Тогда
. Тогда
![]()
Учитывая
произвольность точек
![]() и
и![]() , получаем требуемое утверждение.
, получаем требуемое утверждение.
Геометрическая
интерпретация теоремы Лагранжа.
Разностное отношение в правой части
формулы (13) есть угловой коэффициент
секущей, проходящей через точки
![]() и
и![]() , а производная
, а производная![]() равна угловому коэффициенту касательной
к графику функции
равна угловому коэффициенту касательной
к графику функции![]() в некоторой средней точке промежутка
в некоторой средней точке промежутка![]() . Поэтому за теоремой Лагранжа закрепилось
название “теорема о среднем”.
. Поэтому за теоремой Лагранжа закрепилось
название “теорема о среднем”.
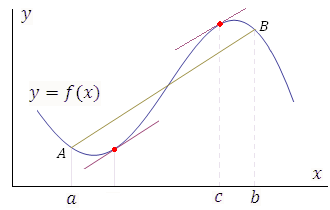
Рис.
6. Теорема Лагранжа устанавливает условия
существования хотя бы одной точки c, в
которой касательная к графику функции
![]() параллельна секущей AB. Таких точек
может быть несколько.
параллельна секущей AB. Таких точек
может быть несколько.
Физическая
интерпретацию теоремы Лагранжа.
Пусть функция
![]() описывает смещение частицы из начального
положения в зависимости от времени x ее
движения по прямой. Тогда разностное
отношение
описывает смещение частицы из начального
положения в зависимости от времени x ее
движения по прямой. Тогда разностное
отношение
![]()
представляет
собой среднюю скорость движения частицы
за промежуток времени
![]() , а производная –
, а производная –![]() мгновенную скорость движения частицы
в момент времени c. Существует такой
момент времени, в который мгновенная
скорость движения равна средней скорости.
мгновенную скорость движения частицы
в момент времени c. Существует такой
момент времени, в который мгновенная
скорость движения равна средней скорости.
Отметим,
что формула (13) сохраняет свою справедливость
и при b < a. Если применить теорему
Лагранжа к промежутку
![]() и представить значение c в виде
и представить значение c в виде![]()
где
![]() то формула (13) примет вид
то формула (13) примет вид![]() (14)
(14)
Равенство (14) дает точное значение для приращения функции при конечном значении приращения аргумента и называется формулой конечных приращений. Единственным недостатком этой замечательной формулы является присутствие в ней неопределенного числа θ. 20. Теорема Коши
