
- •1.Определение функции. Способы и задание функции. Предел функции стремящимся к x0 и плюс минус бесконечности
- •2. Односторонние пределы .
- •4. Первый классический предел
- •6. Бесконечно малая функция
- •7.Сравнение бесконечно малых функций
- •8. Определение непрерывности функции Точки разрыва
- •13.Определение и геометрический смысл дифференциалов
- •14.Приближённое вычисление с помощью дифференциалов
- •16. Понятие дифференцируемости функции данной точки . Связь между понятие дифференцированности и непрерывности
- •17.Теорема Ферма
- •18.Теорема Ролля
- •19. Теорема Лагранжа
- •21. Правила лопиталя
- •22. Признаки монотонности функции
- •23.Достаточные условия локального экстремума
- •24. Необходимое условие локального экстремума Необходимые условия существования локальных экстремумов[править]
- •25. Направление выпуклости и вогнутости графиков функции 26. Точка перегиба графика функции. Необходимое и достаточное условие точки перегиба 27. Асимптоты графика функции
- •28. Понятие первообразной неопределенной функции 29. Основные свойства неопределенного интеграла
- •30. Интегрирование методом замены переменной
- •31. Интегрирование неопределенного интеграла по частям
- •32. Интегрированы рациональной функции
- •33. Интегрирование геометрической функции
1.Определение функции. Способы и задание функции. Предел функции стремящимся к x0 и плюс минус бесконечности
Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Пусть задана числовая функция с неограниченной сверху областью определения, то есть
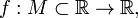 и
и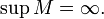 Тогда
Тогда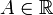 наывается пределом функции
наывается пределом функции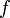 при
при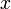 стремящемся
к бесконечности, если
стремящемся
к бесконечности, если
![]()
Пишут:
![]()
Аналогично пусть
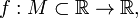 и
и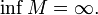 Число
Число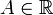 называется
пределом функции
называется
пределом функции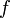 при
при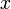 стремящемся
к минус бесконечности, если
стремящемся
к минус бесконечности, если
![]()
Пишут:
![]()
![]()
![]() ,
если r
нечётно,
и
,
если r
нечётно,
и
![]() ,
еслиr
чётно.
,
еслиr
чётно.
2. Односторонние пределы .
Пусть
переменная x стремится к a, оставаясь
больше a, и при этом
![]() . Тогда число A называют правосторонним
пределом (или пределом справа) функции
. Тогда число A называют правосторонним
пределом (или пределом справа) функции![]() и обозначают любым из символических
выражений
и обозначают любым из символических
выражений
![]()
Понятие левостороннего
предела (или предела слева) вводится
аналогичным образом. В этом случае
![]() при x → a со стороны меньших значений:
при x → a со стороны меньших значений:
![]()
Для существования
обычного (двустороннего) предела функции
![]() в точке a необходимо и достаточно
равенство между собой односторонних
пределов:
в точке a необходимо и достаточно
равенство между собой односторонних
пределов:
![]()
![]()
Например, в точке x = 3 односторонние пределы функции
![]()
отличаются друг от друга:
![]()
![]()
Поэтому в
рассматриваемой точке предел функции
![]() не существует.3.
Теоремы о пределах функции
не существует.3.
Теоремы о пределах функции
Приведем без доказательства основные теоремы о пределах функций. Эти теоремы вполне аналогичны тем, которые мы рассматривали (также без доказательства) ранее при изучении пределов числовых последовательностей.
1. Предел константы равен самой этой константе:
![]() с = с.
с = с.
2. Постоянный множитель можно выносить за знак предела:
![]() [ k • f (х)] = k •
[ k • f (х)] = k •
![]() f (х).
f (х).
3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций:
![]() [ f (х) ± g (х)] =
[ f (х) ± g (х)] =
![]() f (х) ±
f (х) ±![]() g (x).
g (x).
4. Предел произведения функций равен произведению пределов этих функций:
![]() [ f (х) • g (х)] =
[ f (х) • g (х)] =
![]() f (х) •
f (х) •![]() g (x).
g (x).
5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:
4. Первый классический предел
Первый замечательный предел:
![]()
5 второй класс предел .
Второй
замечательный пределимеет вид: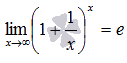
или
в другой записи
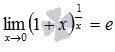
В случае второго
замечательного
предела имеем дело с неопределенностью
вида единица в степени бесконечность
![]() .
.
6. Бесконечно малая функция
Рассмотрим
функцию
![]() ,
определенную в некоторой окрестности
,
определенную в некоторой окрестности![]() точки
точки![]() ,
,![]() , за исключением, быть может, самой точки
, за исключением, быть может, самой точки![]() . Функция
. Функция![]() называется бесконечно малой при
называется бесконечно малой при![]() ,
стремящемся к
,
стремящемся к![]() ,
если
,
если![]() . Если
. Если![]() — бесконечно малая в точке
— бесконечно малая в точке![]() , то для любого положительного числа
, то для любого положительного числа![]() ,
как бы мало оно ни было, существует такое
положительное число
,
как бы мало оно ни было, существует такое
положительное число![]() , что для всех
, что для всех![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству![]() ,
справедливо неравенство
,
справедливо неравенство![]() .
Неравенства
.
Неравенства![]() для всех
для всех![]() , эквивалентные неравенствам
, эквивалентные неравенствам![]() ,
,![]() , означают, что для любого
, означают, что для любого![]() существует такое
существует такое![]() , что для
, что для![]() график функции расположен на плоскости
в прямоугольнике
график функции расположен на плоскости
в прямоугольнике![]() .
Важно, что слова “за исключением, быть
может, самой точки ” означают, что нас
не интересует сама эта точка. Это можно
понять, если рассмотреть функцию
.
Важно, что слова “за исключением, быть
может, самой точки ” означают, что нас
не интересует сама эта точка. Это можно
понять, если рассмотреть функцию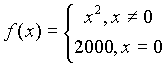 .
При x, стремящемся к нулю, функция-таки
стремится к нулю, независимо от того,
какое значение она принимает в точке
x=0. Следовательно, предел равен нулю и
функция является бесконечно малой.
.
При x, стремящемся к нулю, функция-таки
стремится к нулю, независимо от того,
какое значение она принимает в точке
x=0. Следовательно, предел равен нулю и
функция является бесконечно малой.
