
- •Министерство образования и науки Российской Федерации
- •Содержание
- •Введение
- •1. Современное состояние проблемы моделирования систем
- •1.1. Моделирование как метод научного познания. Философские аспекты моделирования
- •1.2. Использование моделирования при исследовании и проектировании систем
- •1.2.1. Особенности разработки систем
- •1.2.2. Особенности использования моделей
- •1.2.3. Перспективы развития методов и средств моделирования систем
- •2. Основные понятия теории моделирования систем
- •2.1. Принцип системного подхода в моделировании систем
- •2.1.1. Структура системы – совокупность связей между элементами системы
- •2.1.2. Экспериментальные исследования систем
- •2.2. Стадии разработки моделей
- •2.3. Понятие подобия
- •2.3.1. Общие положения
- •2.3.2. Основные понятия теории размерности
- •2.3.3. Примеры подобия
- •2.4. Общая характеристика проблемы моделирования систем
- •2.4.1. Объект моделирования.
- •2.4.2. Характеристики моделей систем
- •2.4.3. Цели моделирования систем
- •2.5. Классификация видов и методов моделирования систем
- •2.5.1. Классификационные признаки
- •2.5.2. Математическое моделирование.
- •2.6. Построение модели
- •2.7. Разработка вычислительного метода
- •2.8. Проверка (тестирование) модели
- •3. Математическое моделирование
- •3.1. Задачи и цели исследования математических моделей
- •3.2. Методология математического моделирования. Системный анализ
- •3.2.1. Понятие системы
- •3.2.2. Этапы системного анализа и декомпозиция
- •3.2.3. Экспертные оценки
- •3.3. Классификация математических моделей
- •3.4. Методы формализованного описания системы
- •3.4.1. Математическая модель по “входу-выходу”
- •3.4.2. Математическая модель в пространстве состояний
- •3.4.3. Описание линейных систем в пространстве состояний
- •3.4.4. Реализация систем в пространстве состояний
- •3.5. Методы построения математических моделей и их применение в сапр
- •3.5.1. Методы построения математических моделей
- •3.5.2. Математические модели с точки зрения сапр
- •3.5.4. Методика составления уравнений динамики элементов сау
- •3.6. Математические модели системы управления. Понятие об оптимальном управлении
- •4. Экспериментальное определение динамических характеристик объектов моделирования
- •4.1. Понятие о динамических характеристиках объектов
- •4.2. Определение динамических характеристик элементов систем по временным характеристикам
- •4.2.1. Определение статических характеристик
- •4.2.2. Определение динамических характеристик объектов с помощью периодических воздействий
- •4.4.1. Временные характеристики и их свойства
- •4.4.2. Определение характеристик апериодического звена
- •4.4.3. Определение характеристик колебательного звена
- •4.3. Формы описания динамических свойств объектов
- •4.4. Синтез пассивных двухполюсников и четырехполюсников
- •4.3.1. Разложение передаточной функции активного четырехполюсника
- •4.3.2. Способы синтеза двухполюсников
- •4.5. Экспериментальная отработка характеристик системы управления движущимся объектом
- •4.5.1. Общие положения
- •4.5.2. Алгоритмы обработки внешнетраекторных измерений
- •5. Динамические свойства воспринимающих элементов и датчиков
- •5.1. Основные определения и понятия
- •5.1.1. Понятие датчика
- •5.1.2. Классификация датчиков
- •5.2. Основные характеристики датчиков
- •5.2.1. Погрешности измерений
- •5.2.2. Чувствительность датчиков
- •5.2.3. Быстродействие датчика
- •5.3. Схемы формирования сигналов пассивных датчиков
- •5.3.1. Общие характеристики
- •5.4. Оптические датчики
- •5.4.1. Определения и основные зависимости
- •5.4.2. Фоторезисторы
- •5.4.3. Фотодиоды
- •5.4.4. Тепловые приемники излучения
- •5.4.5. Датчики изображения
- •5.4.6. Волоконная оптика
- •5.5. Датчики температуры
- •5.5.1. Методы измерения температуры
- •5.6. Датчики положения и перемещения
- •5.6.1. Методы определения положения и перемещения
- •5.6.2. Резисторные потенциометры
- •5.6.3. Индуктивные датчики
- •5.6.4. Емкостные датчики
- •5.6.5. Цифровые датчики
- •5.6.6. Датчики близости
- •5.7. Датчики деформации
- •5.7.1. Основные определения
- •5.7.2. Основные положения
- •5.8. Тахометрические датчики
- •5.8.1. Электродинамическая тахометрия
- •5.8.2. Импульсная тахометрия
- •5.8.3. Гирометры
- •5.9. Датчики ускорения, вибрации и удара
- •5.9.1. Общие положения
- •5.9.2. Принцип действия сейсмических датчиков
- •5.10. Датчики скорости, расхода и уровня жидкости
- •5.10.1. Элементарные понятия
- •5.10.2 Датчики и методы измерения скорости жидкости
- •5.10.3. Измерение расхода жидкости
- •5.10.4. Измерение и указание уровня жидкости
- •5.11. Датчики влажности
- •5.11.1. Определения
- •5.11.2. Гигрометры
- •5.12. Акустические датчики
- •5.12.1. Распространение плоской волны
- •5.12.2. Распространение трехмерной волны
- •5.12.3. Микрофоны
- •5.12.4. Измерение интенсивности
- •6. Основы технологии имитационного моделирования
- •6.1. Основные определения и понятия
- •6.2. Область применения и классификация имитационных моделей
- •6.3. Описание поведения системы
- •6.3.1. Общие положения.
- •6.3.2. Методика моделирования случайных факторов
- •6.3.3. Два подхода к моделированию случайных чисел
- •6.4. Оценка качества псевдослучайных чисел
- •6.5. Оценка качества имитационного моделирования
- •7. Методы испытаний систем управления и их применение в системах автоматизированного проектирования (сапр)
- •7.1. Полунатурное моделирование
- •7.1.1. Общие положения
- •7.1.2. Автоматизация испытаний на основе полунатурного моделирования
- •8. Анализ систем управления с эвм
- •8.1. Основные задачи
- •8.2. Особенности систем управления с эвм
- •8.2. Основные положения из теории дискретных линейных систем
- •8.2.1. Последовательности
- •8.2.2. Линейные системы с постоянными параметрами
- •8.2.3. Разностные уравнения
- •8.2.3.1. Решение разностных уравнений методом прямой подстановки
- •8.3. Расчет цифровых фильтров по фильтрам непрерывного времени
- •8.3.1 Методика синтеза цифровых фильтров. Общие положения
- •8.3.2 Методы дискретизации аналоговых фильтров
- •8.3.3. Геометрическая интерпретация методов расчета цифровых фильтров по фильтрам непрерывного времени
- •9. Моделирование свойств объектов с помощью системыMatLab
- •9.1. Введение
- •9.2. MatLab как научный калькулятор
- •9.2.1. Командное окно
- •9.2.2. Операции с числами
- •9.2.3. Простейшие операции с векторами и матрицами
- •9.2.4. Некоторые функции прикладной численной математики
- •9.2.5. Построение простейших графиков
- •9.3. Исследование линейных стационарных систем (лсс)
- •9.3.1. Классы пакета control.L
- •9.3.2. Ввод и преобразование моделей
- •Пример создания модели
- •9.3.3. Анализ системы
- •9.4. Моделирование динамических процессов с помощью подсистемы MatLab simulink
- •9.4.1. Краткие сведения о подсистеме MatLab simulink
- •9.4.2. Запуск подсистемы simulink
- •9.4.3. Создание модели
- •9.4.4. Некоторые основные приемы подготовки и редактирования модели
- •9.4.5. Установка параметров моделирования и его выполнение
- •9.2.2. Результат составления модели
- •Приложения п1. Динамические характеристики объектов моделирования
- •П2. Примеры составление функциональной и структурной схемы динамической системы
- •П2.1. Система управления угловой скорости вращения ротора двигателя при условии действия постоянного возмущения
- •П2.2. Система сопровождения цели
- •П2.3. Система автоматического наведения летательного аппарата на объект
- •П2.4. Система управления уровнем жидкости
- •П2.5. Система управления экономическими параметрами
- •Использованные источники
- •Основы теории и практики моделирования динамических систем
8.3.2 Методы дискретизации аналоговых фильтров
Наиболее распространенными методами дискретизации аналогового фильтра с передаточной функцией вида (8.34) являются следующие:
- метод отображения дифференциалов;
- метод инвариантного преобразования импульсной характеристики;
- метод билинейного преобразования;
- метод согласованного z –преобразования.
8.3.2.1. Метод отображения дифференциалов
Это один из наиболее простых методов дискретизации. Заключается в замене дифференциалов в ее дифференциальном уравнении на конечные разности, что позволяет получить разностное уравнение, аппроксимирующее исходное дифференциальное уравнение.
При этом производится замена дифференциалов простыми разностями путем подстановки типа
![]() или
или
![]() (8.36)
(8.36)
и непосредственно
переходят от рациональной передаточной
функции от
![]() к рациональной передаточной функции
от
к рациональной передаточной функции
от![]() .
.
При этом, однако, характеристики аналогового фильтра не сохраняются. Поэтому данный метод применяется редко.
8.3.2.2. Метод инвариантного преобразования импульсной характеристики
Разложим передаточную функцию фильтра (8.34) на простые дроби
![]() ,
,
где
![]() - полюсы;
- полюсы;
![]() .
.
Переход от
![]() к
к![]() осуществляется с помощью отображения,
при котором используется замена
осуществляется с помощью отображения,
при котором используется замена
![]() .
(8.37)
.
(8.37)
8.3.2.3. Метод билинейного преобразования
При этом используется замена
![]() ,
(8.38)
,
(8.38)
что
приводит к связи между передаточными
функциями
![]() к
к![]()
![]() .
.
Это простое
конформное отображение
![]() -плоскости
в
-плоскости
в![]() -плоскость,
свободное от недостатков первого
метода и в то же время сохраняет удобную
алгебраическую форму преобразования.
-плоскость,
свободное от недостатков первого
метода и в то же время сохраняет удобную
алгебраическую форму преобразования.
8.3.2.4. Метод согласованного z –преобразования
При этом методе отображающая замена будет иметь вид
![]() .
(8.39)
.
(8.39)
Метод прост, но во многих случаях не применим из-за искажения во многих случаях положения нулей цифрового фильтра.
8.3.2.5. Универсальный метод
При переходе к
дискретному времени в передаточной
функции
![]() системы нужно произвести замену [6]
системы нужно произвести замену [6]
![]() .
(8.40)
.
(8.40)
Метод прост и дает быстрый результат.
8.3.3. Геометрическая интерпретация методов расчета цифровых фильтров по фильтрам непрерывного времени
Как отмечено выше, определение параметров цифрового фильтра осуществляется путем пересчета параметров непрерывного фильтра.
И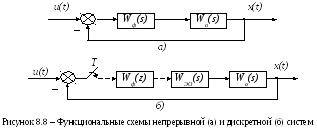 дея
такой замены можно пояснить рис. 8.8.
Здесь замкнутая система с непрерывным
объектом управленияc
передаточной функцией W0(s)
и синтезированным непрерывным фильтром
с передаточной функцией Wф(s)
(рис. 8.8, а) преобразовывается в
систему с цифровым фильтром Wф(z)
и фиксатором вычислений ЦАП с передаточной
функцией
дея
такой замены можно пояснить рис. 8.8.
Здесь замкнутая система с непрерывным
объектом управленияc
передаточной функцией W0(s)
и синтезированным непрерывным фильтром
с передаточной функцией Wф(s)
(рис. 8.8, а) преобразовывается в
систему с цифровым фильтром Wф(z)
и фиксатором вычислений ЦАП с передаточной
функцией
![]() (рис. 8.8, б).
(рис. 8.8, б).
Преобразование базируется на представлении интеграла суммой. Эта сумма может быть вычислена различными способами.
Прямой метод Эйлера.
П рямой
метод Эйлера демонстрируется рис. 8.8.
рямой
метод Эйлера демонстрируется рис. 8.8.
Значение выходного сигнала x(t) в момент t=nT здесь находится из выражения
![]() .
(8.41)
.
(8.41)
При подстановке оператора задержки (см. (8.31)) в выражение (8.41) получим:
![]() .
(8.42)
.
(8.42)
Из (8.42) следует, что сигнал на выходе может быть представлен в виде:
![]() .
(8.43)
.
(8.43)
Таким
образом, при использовании прямого
метода Эйлера осуществляется замена
переменной оператора интегрирования
![]() через оператор задержки
через оператор задержки![]() .
Соответствующее выражение замены имеет
вид:
.
Соответствующее выражение замены имеет
вид:
![]() .
или
.
или
![]() . (8.44)
. (8.44)
Из рассмотрения выражения (8.44) следует, что оно совпадает с выражением (8.40) для универсального метода дискретизации.
Обратный метод Эйлера.
Данный метод иллюстрируется рис. 8.10.
Значение выходного сигнала x(t) в момент t=nT здесь находится из выражения
![]() .
(8.45)
.
(8.45)
При подстановке оператора задержки получим
![]() .
(8.46)
.
(8.46)
Отсюда следует, что сигнал на выходе может быть представлен в виде
![]()
 .
(8.47)
.
(8.47)
Таким образом, при этом методе осуществляется замена переменных следующим образом
![]()
 .
или
.
или
![]() . (8.48)
. (8.48)
Выражение (8.48) совпадает с выражением (8.36), т. е. обратный метод Эйлера иллюстрирует метод отображения дифференциалов.
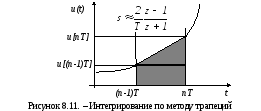
Метод трапеций.
Интегрирование по данному методу иллюстрируется рис. 8.11.
Значение выходного сигнала x(t) в момент t=nT здесь находится из выражения
![]() .
(8.49)
.
(8.49)
После подстановки оператора задержки в выражение (8.49) получим сигнал на выходе, который определится по зависимости:
![]() .
(8.50)
.
(8.50)
В
этом случае аналогом оператора
интегрирования
![]() является оператор,
является оператор,
![]() или
или
![]() ,
(8.51)
,
(8.51)
который соответствует выражению метода билинейного преобразования (8.38).
Очевидно, что данное преобразование обеспечивает более высокую точность замены, сохраняя характеристики аналогового фильтра. Это вытекает из геометрической интерпретации метода: замена элемента площади под непрерывной кривой трапецией (в последнем случае) обеспечивает более высокую точность такой замены прямоугольниками (в случаях прямого и обратного методов Эйлера).
В силу сказанного метод билинейного преобразования является предпочтительным.
Таким образом, если известна операторная передаточная функция непрерывного фильтра, то, используя различные методы численного интегрирования, можно определить передаточную функцию цифрового фильтра.
При этом необходимо заметить, что последняя зависит не только от способа численного интегрирования, но и от значения периода дискретизации Т.
