5. Динамические свойства воспринимающих элементов и датчиков

5.1. Основные определения и понятия

5.1.1. Понятие датчика

Физическая величина m, характеризующая объект измерений (температуру, давление, и др.), называется измеряемой величиной [1, 2].

Датчик – это устройство, которое, подвергаясь воздействию физической измеряемой величины m, выдает эквивалентный сигнал , обычно электрической природы, являющийся функцией измеряемой величины (см. рисунок 5.1).

Х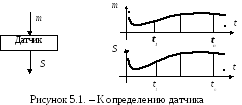арактеристика такого преобразованияможет быть в формальном виде представлена соотношением

(5.1)

где - выходная величина датчика;

- входная величина.

Для всех датчиков характеристика преобразования - соотношение (5.1) – в численной форме определяется экспериментально в результате градуировки, что позволяет построить градуированную кривую. Для этого при известных значениях физической величины m снимают соответствующие показания датчика: и строят зависимость.

Рисунок 5.2 поясняет алгоритм получения характеристики преобразования датчика.

А по известной характеристике датчика и его показаниям легко получить значения физической величины:

На практике стремятся, чтобы существовала линейная зависимость между малыми приращениями выходной и входнойвеличин да датчика

. (5.2)

Здесь - чувствительность датчика. Обеспечение линейности означает.

В общем случае на практике обеспечение постоянства является проблемой.

5.1.2. Классификация датчиков

Датчики с точки зрения вида сигнала на выходе могут быть:

активными – генератором, выдающим заряд, напряжение или ток, либо

пассивными – с выходным сопротивлением, индуктивностью или емкостью, изменяющимися в соответствии с входной величиной.

Активные датчики

Принцип действия активного датчика основан на том или ином физическом явлении, обеспечивающем преобразование измеряемой величины в электрическую форму.

В таблице 5.1 приведены физические эффекты, наиболее часто используемые для построения активных датчиков.

Таблица 5.1. Измеряемые датчиками величины и физические эффекты, используемые при построении активных датчиков

Измеряемая величина	Используемый эффект	Выходная величина датчика
Температура	Термоэлектрический эффект (термопара)	Напряжение
Сила, давление, ускорение	Пьезоэлектрический эффект	Заряд
Скорость	Электромагнитная индукция	Напряжение

Вкратце рассмотрим перечисленные в таблице эффекты.

1. Термоэлектрический эффект

Схема, поясняющая этот эффект, представлена на рисунке 5.3.

Н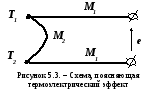а рисункеM₁, M₂ – два проводника различного химического состава; их спаи, находящиеся при температурах T₁, T₂, являются местом возникновения термо-э.д.с. e: e = e (T₁, T₂). Термо-э.д.с. пропорциональна измеряемой разнице температур (T₁ - T₂): e  e (T₁ - T₂).

2. Пьезоэффект

Пьезоэффект проявляется в том, что при изменении механического напряжения в кристалле пъезоэлектрика, например, кварца (см. рисунок 5.4) под действием приложенной к нему силы F приводит к деформации, которая вызывает появление на противолежащих поверхностях кристалла одинаковых по величине электрических зарядов противоположного знака, и, следовательно, появление электрического напряжения v: .

П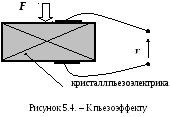ри этом существует очевидное соотношениеv  F.

Таким образом, измерение силы F или приводимых к ней величин (давление, ускорение) осуществляется измерением напряжения v между зажимами пьезоэлектрика.

3. Эффект электромагнитной индукции

Явление электромагнитной индукции заключается в том, что при перемещении проводника в постоянном электромагнитном поле с вектором магнитной индукции возникает э.д.с.e , пропорциональная магнитному потоку, и, следовательно, скорости перемещения. Соответствующая схема, поясняющая данный эффект, приведена на рисунке 5.5, где  - скорость вращения проводящего контура.

Зависимость между скоростью , магнитной индукцией B и э.д.с. e может быть получена из выражения .

Пассивные датчики

В пассивных датчиках некоторые параметры выходного импеданса могут меняться под воздействием измеряемой величины.

Импеданс датчика, с одной стороны, обусловлен геометрическими размерами его элементов, а с другой – свойствами материалов: удельным сопротивлением , магнитной проницаемостью , и диэлектрической постоянной 

В таблице 5.2 приведены физические принципы преобразования величин и материалы, используемые для построения пассивных датчиков.

Таблица 5.2. Физические принципы преобразования величин и материалы, используемые для построения пассивных датчиков

Измеряемая величина	Электрическая характеристика, изменяющаяся под действием измеряемой величины	Тип используемых материалов
Температура	Сопротивление	Металлы, полупроводники
Деформация	Сопротивление	Сплавы никеля, легированный кремний
Перемещение	Сопротивление	Магниторезистивные материалы
Плотность	Сопротивление	Хлористый литий, окись алюминия

Импеданс пассивного датчика и его изменения можно измерить не иначе, как включая датчик в специальную электрическую схему, содержащую источник питания и схему формирования сигнала.

Комбинированные датчики

При измерениях некоторых неэлектрических величин не всегда удается преобразовать их непосредственно в электрическую величину.

В этих случаях осуществляется двойное преобразование исходной (первичной) измеряемой величины в промежуточную, которую затем преобразуют в электрическую.

Б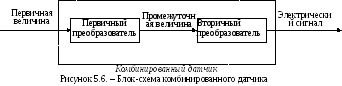лок схема комбинированного датчика в общем случае можно представить в виде, приведенном на рисунке 5.6.