3.5.2. Математические модели с точки зрения сапр

Математическое обеспечение САПР включает в себя математические модели объектов проектирования, методы и алгоритмы.

М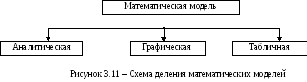атематические модели - это система математических соотношений: аналитических в виде уравнений, графических в виде структурных схем или графов, табличных в виде таблиц. Соответствующая условная схема такого деления моделей представлена на рисунке 3.11.

Метод (греч. methodos) - путь исследования задачи, включающая в себя совокупность теории и приемов, содержащих логику и обоснование решения задачи.

Из метода вытекает алгоритм. Алгоритм (лат. algorithmi) – от арабской интерпретации имени узбекского математика IX века в Аль-Хорезми, означает совокупность правил, определяющих процедуру решения задачи по заданным исходным данным, которая заканчивается результатом, решением.

Вычислительный алгоритм - строится по известному алгоритму и представляет собой последовательность арифметических, логических и аналитических операций, составленных с учетом возможностей реализации на ЭВМ и оценкой погрешностей вычислений.

На математическом обеспечении как на фундаменте строятся основные компоненты САПР – пакеты прикладных программ (ППП).

В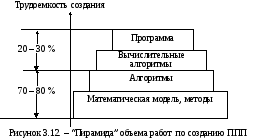есьобъем работ по созданию ППП можно представить условно в виде следующей “пирамиды” (рисунок 3.12).

Математическую модель также можно классифицировать по степени детализации в соответствии с трехуровневой иерархической схемы (см. рисунок 3.13).

Н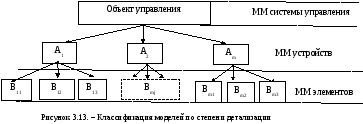а самом верхнем уровне наибольшее распространение в теории получили математические модели в виде структурных схем и графов.

Структурная схема - это ее графическое изображение в виде соединения звеньев.

Типовая структурная схема представлена ниже на рисунке 3.14.

Она содержит:

1 – сумматоры (места суммирования одинаковых физических величин);

2 – динамические звенья в виде прямоугольников, свойсва звеньев описываются дифференциальными, алгебраическими уравнениями;

3 – узел (место расщепления сигнала);

4 – линии (условная связь между какими-либо элементами; стрелка означает, что обратное влияние звеньев друг на друга практически отсутствует, либо оно пренебрежительно мало).

У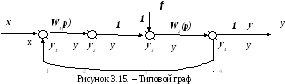добным для исследования отображением структурных схем являетсяортиентированные графы, которые оболадают следующими свойствами:

- дуги графов изображают звено и характеризуются опенратором звена – уравнением звена, передаточной функцией;

- каждой вершине ставится одна из переменных, и в соответствии с правилами работы с графами вершина, к которой подходит одна или несколько дуг, соответствует переменной, равной выходу одной дуги или сумме выходов дуг. Если из вершины исходит несколько дуг, то входная величина для всех этих дуг одно и то же. Граф, эквивалентный структурной схеме, представленной на рисунке 3.14, приведен на рисунке 3.15.

3.5.3. Методы упрощения моделей

Основная цель при построени математческтх моделей – это получение математической модели, соответствующей целям исследования, достигается путем упрощения и преобразования полной ММ.

Упрощение ММ – это проектная процедура П преобразования исходной математической модели М в упрощенную модель М_i, эквивалентную М с точки зрения цели исследования.

Можно выделить основные подходы к решению задачи упрощения ММ. Это:

- редукция;

- декомпозиция.

Редукция

Схема процедуры выглядит следующим образом

,

.

Исходная модель М последовательно редуцируется к упрощенным моделям М_i меньшей сложности .

Эта процедура предполагает исключения, не влияющие на результат исследования и расчетов составляющих математической модели.

Декомпозиция

Схему процедуры можно представить следующим образом:

, ,

где - некоторая мера сложности ММ (например, порядок системы уравнений, число слагаемых, время счета и т.д.)

Эта операция предполагает возможность разбиения исходной ММ на ряд частных моделей.

Эти подходы могут быть реализованы при помощи ряда методов.

Метод возмущений.

Основой метода является положение, что некоторые динамические связи в модели могут игнорироваться, т.е. исходная модель может апроксимироваться моделью, структура которой проще.

Пример

Пусть система описывается следующим матричным уравнением в пространстве состояний

,

где A, Z, B, U – матрицы.

Для простоты рассмотрим случай уравнений второго порядка. Пусть имеем

,

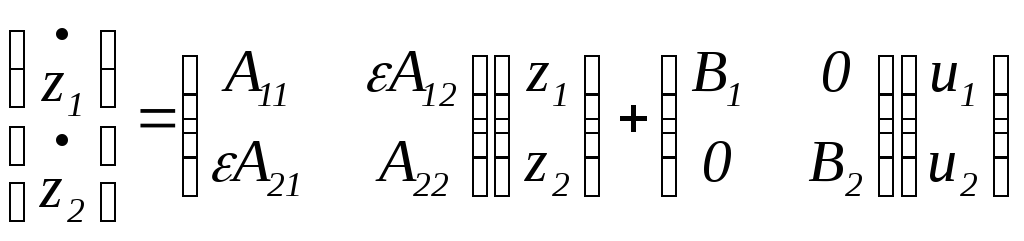где ,- фазовые координаты;

- элементы матрицы состояния;

, - элементы матрицы управления;

, - элементы вектора управления;

>0 – некоторый параметр.

Представленному матричному уравнению соответствует следующая система уравнений:

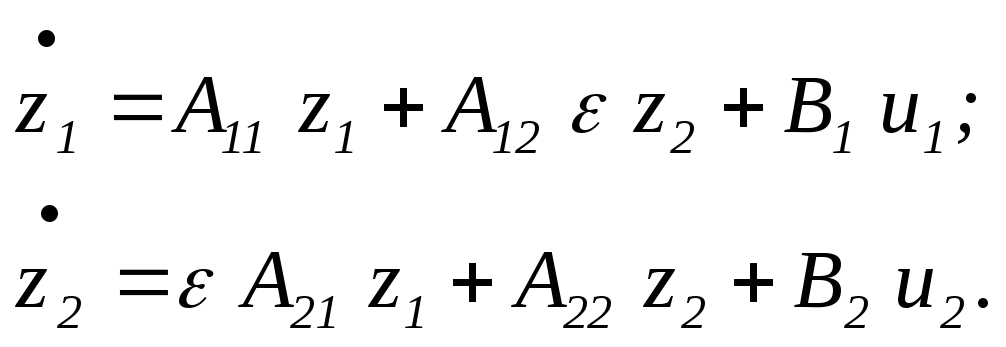
Если параметр мал (т.е.), то система распадается на 2 независимые подсистемы меньшей размерности (первого порядка).

Метод линеаризации

Одна из особенностей математических моделей в общем случае – это их нелинейность.

Поэтому наиболее эффективный метод упрощения моделей в этом случае – метод линеаризации.

Пример.

Для нелинейной системы часто удается подобрать некоторую линейную модель, достаточно адекватно описывающую свойства исходной САУ. Процедуру замены нелинейной модели САУ некоторой приближенной линейной моделью называют линеаризацией.

Существует достаточно большое количество видов линеаризации.

Наиболее простой вариант линеаризации нелинейной модели - это построение линейного приближения в малой окрестности некоторой опорной точки путем разложения в степенной ряд.

Пусть САУ описывается моделью в виде нелинейного дифференциального уравнения

, (3.20)

где - входное воздействие,- выходная величина. Здесь же в качестве

(3.21)

обозначены соответствующие производные функций и.

Если функцию (3.20) можно разложить в степенные ряды, то линеаризация осуществляется с использованием формулы для линейного приращения

. (3.22)

Линеаризация производится вблизи какой-то опорной точки в ее малой окрестности. С помощью линейной функции (3.22) уравнение (3.20) превращается в линейное дифференциальное уравнение вида

=

=. (3.23)

Звездочка в частных производных означает, что их необходимо вычислять в какой-то опорной точке

(3.24)

с постоянными координатами

В качестве примера линеаризуем нелинейное дифференциальное уравнение

.

Находим частные производные

, ,,,.

Возьмем в качестве примера опорную точку

.

В этой точке частные производные имеют следующие значения:

, ,,,.

Как следствие, исходное уравнение после линеаризации принимает общий вид:

=,

а с учётом значений частных производных

.

Полученное линейное дифференциальное уравнение не может точно описывать свойства исходной нелинейной системы во всем диапазоне изменений координат и, а справедливотолько в малых окрестностях опорной точки.

Машинно-аналитический метод

Ряд преимуществ с точки зрения машинной реализации имеют методы упрощения, сводящие дифференциальные уравнения к системе конечных, в частности, алгебраических уравнений.

Один из таких методов – машинно-аналитический метод.

Сущность метода сводится к следующему.

Пусть математическая модель задана в форме:

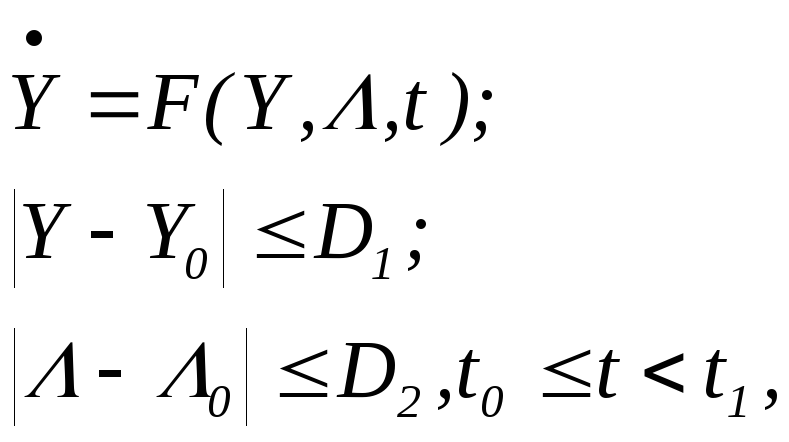(3.25)

где - заданная в областиD вещественная функция от Y, Λ, t;

Y (t) = [y₁(t), y₁(t), …, y_n(t)] - вектор-функция от фазовых координат системы;

Λ(t) = [λ₁(t), λ ₂(t), …, λ _n(t)] - - вектор, составленный из параметров системы, включая входные сигналы и начальные условия;

- полученные на ЭВМ в результате численного решения фазовые координаты.

В соответствии с машинно-аналитическим методом “машинные решения” исходной системы аппроксимируются аналитическими функциями и представляются в виде

(3.26)

где S(s₁, s₂, ..., s_n) – вектор, составленный из характеристик процессов – параметров аппроксимирующих функций φ (t,S); например, вектор из n и Ω в функциях e^nt, sin (Ωt), e^ntsin (Ωt).

По исходным уравнениям (3.25) и аппроксимациям машинных решений (3.26) в результате определенного процесса последовательных приближений в аналитическом виде получают зависимость

Ф(S, Λ, t) = 0, (3.27)

связывающую характеристики процесса в системе с ее параметрами. Эта зависимость называется определяющим уравнением.

Уравнения (3.27) могут быть также использованы для упрощения исходных дифференциальных уравнений (3.25) путем их редукции – исключения малозначащих в смысле цели их применения членов уравнений, параметров.

В этом случае по зависимостям (3.27) (определяющим уравнениям) при условии

строится матрица чувствительности характеристик процессов к изменению параметров Λ.

Для этого найдем дифференциал путем дифференцирования выражения (3.27) (определения полной производной):

.

Отсюда получим

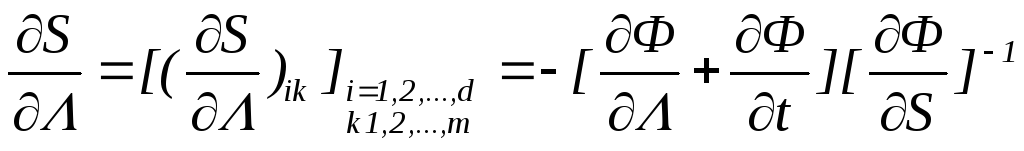. (3.28)

Так как параметры САУ имеют различные размерности и значительные диапазоны изменения, то удобнее пользоваться логарифмическими коэффициентами чувствительности

и .

В соответствии с матрицей чувствительности (3.28) осуществляется редукция исходной модели (3.25) и построение k-го приближения упрощенной эквивалентной модели

.

При этом должны быть заданы диапазоны изменения и точность определения каждого из параметров Λ исходной системы и критерий оценки близости исходной и эквивалентной моделей.

В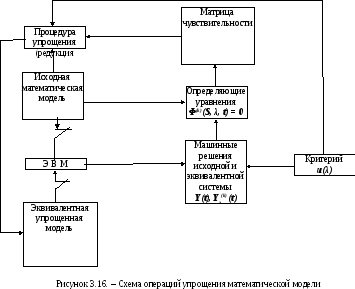качестве такого критерия выбираются математическое ожидание квадрата разности векторовY и Y_э

(3.29)

в течение заданного промежутка времени 0 ≤ t < T.

Схема операций упрощения математической модели на основе соотношений (3.25) – (3.29) может быть представлена в виде, приведенном на рисунке 3.16.