8. 6.3. Нелинейные разветвленные списки

   1. 6.3.1. Основные понятия

Нелинейным разветвленным спискомявляется список, элементами которого могут быть также списки. В разделе 6.2 были рассмотрены двухсвязные линейные списки. Если один из указателей каждого элемента задает порядок, обратный к порядку, устанавливаемому другим указателем, то такой двусвязный список будет линейным. Однако если один из указателей задает порядок произвольного вида, не являющийся обратным по отношению к порядку, устанавливаемому другим указателем, то такой список будет нелинейным.

В обработке нелинейный список определяется как любая последовательность атомовиподсписков, где в качестве атома берется любой объект, который при обработке отличается от списка тем, что он структурно неделим. Если заключим списки в круглые скобки, а элементы списков разделим запятыми, то в качестве списков можно рассматривать такие последовательности:

(a,(b,c,d),e,(f,g))

( )

((a))

Первый список содержит четыре элемента: атом a, список (b,c,d), содержащий в свою очередь атомы b,c,d, атом e и список (f,g), элементами которого являются атомы f и g. Второй список не содержит элементов, тем не менее, нулевой список, в соответствии с определением является действительным списком. Третий список состоит из одного элемента: списка (a), который в свою очередь содержит атом а.

Другой способ представления, часто используемый для иллюстрации списков, – графические схемы, аналогичен способу представления, применяемому при изображении линейных списков. Каждый элемент списка обозначается прямоугольником; стрелки или указатели показывают, являются ли прямоугольники элементами одного и того же списка или элементами подсписка. Пример такого представления показан на рис. 6.11.

a

nil

e

b

g

nil

c

d

nil

f

Рис. 6.11. Схематическое представление разветвленного списка.

Разветвленные списки описываются тремя характеристиками: порядком, глубиной и длиной.

Порядок. Над элементами списка задается транзитивное отношение, определяемое последовательностью, в которой элементы появляются внутри списка. В списке (x,y,z) атом x предшествует y, а y предшествует z. При этом подразумевается, что x предшествует z. Данный список не эквивалентен списку (y,z,x). При представлении списков графическими схемами порядок определяется горизонтальными стрелками. Горизонтальные стрелки истолковываются следующим образом: элемент, из которого исходит стрелка, предшествует элементу, на который она указывает.

Глубина. Максимальный уровень, приписываемый элементам внутри списка или внутри любого подсписка в списке. Уровень элемента описывается вложенностью подсписков внутри списка, т.е. числом пар круглых скобок, окаймляющих элемент.

В списке, изображенном на рис. 6.11, элементы a и e находятся на уровне 1, в то время как оставшиеся элементы – b, c, d, f и g имеют уровень 2. Глубина входного списка равна 2. При представлении списков схемами концепции глубины и уровня облегчаются для понимания, если каждому атомарному или списковому узлу приписать некоторое число l. Значение l для элемента x, обозначаемое как l(x), является числом вертикальных стрелок, которое необходимо пройти для того, чтобы достичь данный элемент из первого элемента списка. Для нашего примера l(a)=0, l(b)=1 и т.д. Глубина списка является максимальным значением уровня среди уровней всех атомов списка.

Длина – число элементов уровня 1 в списке. Например, длина списка нашего примера равна 3.

Типичный пример применения разветвленного списка – представление алгебраического выражения в виде списка. Алгебраическое выражение можно представить в виде последовательности элементарных двухместных операций вида:

< операнд 1 > < знак операции > < операнд 2 >

Выражение (a+b)*(c-(d/e))+f

будет вычисляться в следующем порядке:

a+b

d/e

c-(d/e)

(a+b)*(c-d/e)

(a+b)*(c-d/e)+f

При представлении выражения в виде разветвленного списка каждая тройка «операнд-знак-операнд» представляется в виде списка, причем, в качестве операндов могут выступать как атомы – переменные или константы, так и подсписки такого же вида (рис. 6.12). Скобочное представление выражения будет иметь вид:

(((a,+,b),*,(c,-,(d,/,e)),+,f)

Глубина списка равна 4, длина - 3.

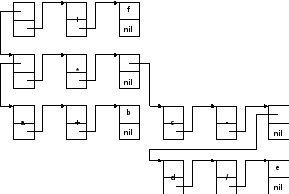
Рис. 6.12. Схема списка, представляющего алгебраическое выражение.