5. Поле объемно заряженного шара

Шар заряжен с постоянной объемной плотностью.

Поле вне шара будет такое же, как у поверхностно-заряженной сферы Е = (как у точечного заряда).

Рассмотрим поле внутри шара (r < R). N = ES = Е4πr².

По теореме Гаусса . Е4πr² = , Е =. Подставим выражение для ρ, Е ==внутри шара напряженность поля линейно растет с увеличением r.

Теорема Гаусса в дифференциальной форме

Теорема Гаусса связывает значения вектора Е в точках замкнутой поверхности, с величиной заряда, находящегося внутри объема, ограниченного этой поверхностью, то есть, связывает величины, относящиеся к разным точкам поля. Для того, чтобы эти величины относились к одной и той же точке поля нужно применить эту теорему к бесконечно малому объему.

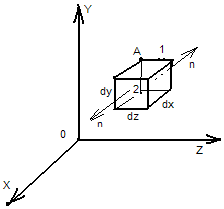Рассмотрим бесконечно малый объем в виде параллелепипеда со сторонами параллельными осям координат, с вершиной в т.А. Вычислим поток вектора напряженности через его поверхность.

Поток через грань 1: N₁ = E_xdS cos α = - E_xdydz (α = π, cos π = -1).

Поток через грань 2: N₂ = (E_x + dE_x)dS cos α = (E_x +dE_x)dydz = (E_x + dx)dydz.

Общий поток через грани вдоль оси Х: N_x = N₁ + N₂ = -E_xdydz + (E_x + dx)dydz =dxdydz =dV.

Аналогично вдоль оси Y и Z. Общий поток через поверхность: N = N_x + N_y + N_z = dV + dV + dV = ( + + )dV. Если в этом объеме распределен заряд с объемной плотностью ρ, то замкнутая поверхность охватывает заряд q = ρdV, следовательно: ( + + )dV = . Сократив обе части уравнения на dV получимтеорему Гаусса в дифференциальной форме или уравнение Пуассона: ( + + ) = .

В векторном анализе доказывается, что предел отношения потока какого-либо вектора А через замкнутую поверхность к величине объема, ограниченного этой поверхностью, при ΔV → 0 не зависит от формы поверхности и называется расхождением или дивергенцией вектора А. .

Пользуясь этим понятием уравнение Пуассона можно записать: .

Лекция 3

Потенциал электростатического поля

Н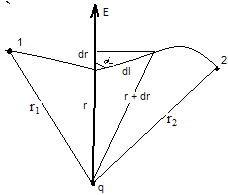а зарядq^* в электрическом поле действует сила F = q^*E. При перемещении заряда эта сила совершает работу. На отрезке dl работа: dA = Fdl cos α = Fdr, А = .

Работа по перемещению заряда q^* не зависит от траектории движения, а определяется только положением начальной и конечной точек перемещения. Силовое поле, обладающее таким свойством, называется потенциальным. Работа сил такого поля может быть представлена как убыль потенциальной энергии: А = W₁ – W₂.

У нас работа: А = . Сопоставляя эти выражения видим, что выражение для потенциальной энергии заряда q^* в поле заряда q имеет вид:

W_п = , где С – произвольная постоянная. Значение С выбирается таким образом, чтобы на бесконечном расстоянии W_п = 0. следовательно, С = 0.

Разные пробные заряды q^* в одной и той же точке поля будут обладать разной потенциальной энергией. Но отношение потенциальной энергии к величине пробного заряда будет величиной постоянной для данной точки поля. Эта величина называется потенциалом поля: . Потенциал является энергетической характеристикой электрического поля, характеризует возможность поля совершать работу.

А = W₁ – W₂ = = q^*(φ₁ – φ₂), если r₂ = ∞, А = q^*φ₁, φ₁ = .

Потенциал данной точки поля численно равен работе по перемещению единичного положительного заряда из данной точки поля в бесконечность.

Размерность потенциала: .

Если поле создано несколькими зарядами, то потенциал его равен алгебраической сумме потенциалов полей, созданных каждым зарядом в отдельности. (Потенциал поля диполя φ = φ₊ + φ_- = ).

Графически распределение потенциала в электрическом поле можно изображать с помощью эквипотенциальных поверхностей. Эквипотенциальная поверхность – это совокупность точек поля, имеющих одинаковый потенциал. Для точечного заряда эквипотенциальные поверхности – сферы, r = const.

Связь между напряженностью и потенциалом

Рассмотрим работу поля при перемещении заряда по эквипотенциальной поверхности на малое расстояние dl. dA = q^*(φ₁ – φ₂) = 0, так как φ₁ = φ₂.

С другой стороны dA = Fdl cos α = q^*Edl cos α = 0, α – угол между вектором Е и направлением перемещения. Так как заряд и перемещение не равны 0, следовательно, cos α = 0, α = 90⁰. Вектор Е перпендикулярен к эквипотенциальной поверхности (силовые линии и эквипотенциальные поверхности взаимно перпендикулярны).

Рассмотрим две близкие эквипотенциальные поверхности φ₁ и φ₂ = φ₁ + dφ, пробный заряд перемещается по силовой линии (1-2).

dA = Fdr = q^*Edr, (cos α = 1). Эту же работу можно определить через разность потенциалов: dA = q^*(φ₁ – φ₂) = q^*(φ₁ – (φ₁ + dφ)) = - q^* dφ

q^*Edr = - q^* dφ, Е = - ,- градиент потенциала, характеризует быстроту изменения потенциала в пространстве. Это вектор, направленный в сторону возрастания потенциала. Вектор напряженности численно равен градиенту потенциала и направлен в сторону убывания потенциала.

Выберем произвольную ось Х и рассмотрим работу поля на пути dx.

dA = Fdx cos α = q^*Edx cos α = q^*E_x dx, также dA = - q^* dφ, q^*E_x dx = - q^* dφ

E_x = - . Аналогичное выражение можно получить для любого направления.

Вектор Е можно выразить через его составляющие: Е = iE_x + jE_y + kE_z, или Е = - (). Пользуясь этим выражением по известным значениям φ можно найти Е в каждой точке поля. Но можно решать и обратную задачу: по известным значениям Е найти разность потенциалов между двумя произвольными точками поля.

А_1,2 = , также А_1,2 = q^*(φ₁ – φ₂), следовательно: φ₁ – φ₂ = . Интеграл можно брать по любой линии, соединяющей точки 1 и 2. если брать по замкнутому контуру, то φ₁ = φ₂ и = 0 – это выполняется только для электростатического поля. В однородном поле, если линияl совпадает с направлением вектора Е φ₁ – φ₂ = Еl , или U = Еl, где U = φ₁ – φ₂ – напряжение.