
- •Лекция 1.
- •Закон Кулона
- •Напряженность электрического поля
- •Электрический диполь
- •Теорема Гаусса
- •Практическое применение теоремы Гаусса
- •5. Поле объемно заряженного шара
- •Теорема Гаусса в дифференциальной форме
- •Потенциал электростатического поля
- •Физические основы электрографии Биопотенциалы
- •Электрокардиография. Теория Эйнтховена
- •Проводники в электрическом поле
- •Поле в диэлектриках. Вектор поляризации и вектор электрического смещения.
- •Поле на границе раздела диэлектриков
- •Пьезоэлектрический эффект
- •Сегнетоэлектрики
- •Электроемкость проводников
- •Конденсатор
- •Соединение конденсаторов
- •Энергия электрического поля
- •Постоянный электрический ток
- •Закон Ома для участка цепи
- •Сверхпроводимость
- •Работа и мощность тока
- •Лекция 7 Закон Ома для замкнутой цепи
- •Разветвленные цепи. Правила Кирхгофа.
- •Механизмы проводимости электрического тока
- •Закон Ома с точки зрения электронной теории металлов
- •Электропроводность жидкостей (электролитов)
- •Законы электролиза
- •Токи в газах. Аэроионы.
- •Диэлектрики, полупроводники, металлы в свете зонной теории
- •Металлы
- •Прмесная проводимость полупроводников
- •Магнитное поле
- •Закон Ампера
- •Напряженность магнитного поля
- •Закон Био-Савара-Лапласа
- •Напряженность поля бесконечно длинного проводника с током
- •Циркуляция вектора напряженности магнитного поля
- •Магнитное поле соленоида
- •Магнитный момент контура с током
- •Магнитное поле в веществе
- •Природа магнитных свойств тел
- •Парамагнетики
- •Диамагнетики
- •Ферромагнетики
- •Электромагнитная индукция Магнитный поток
- •Явление электромагнитной индукции
- •Природа возникновения эдс индукции при движении проводника в магнитном поле
- •Вихревое электрическое поле
- •Самоиндукция
- •Взаимоиндукция
- •Энергия магнитного поля
- •Процессы в колебательном контуре
- •Цепи переменного тока
- •Импеданс тканей организма
- •Взаимные превращения электрического и магнитного полей
- •Ток смещения
- •Уравнения Максвелла
- •Уравнения Максвелла в интегральной форме
- •Уравнения Максвелла в дифференциальной форме
- •Электромагнитные волны
- •Свойства электромагнитных волн
- •Энергия электромагнитной волны
Работа и мощность тока
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Эту работу принято называть работой тока.
Пусть за время t через поперечное сечение проводника проходит заряд q. Тогда электрическое поле совершит работу А = Uq, где U – напряжение на данном участке цепи. Так как q = It , то A = UIt.
По закону сохранения
энергии эта работа должна быть равна
изменению энергии рассматриваемого
участка цепи. В случае, если на участке
не совершается механическая работа
(проводник неподвижен) и ток не производит
химических действий, происходит только
нагревание проводника. Нагретый проводник
отдает теплоту окружающим телам.
Следовательно,
![]() .
.
Закон, определяющий
количество теплоты, которое проводник
с током выделяет в окружающую среду,
был экспериментально установлен
английским ученым Джоулем и русским
ученым Ленцем. Закон Джоуля-Ленца был
сформулирован следующим образом:
количество теплоты, выделяемое проводником
с током, равно произведению квадрата
силы тока, сопротивления проводника и
времени:
![]() .
.
Любой электрический
прибор рассчитан на потребление
определенной энергии в единицу времени.
Поэтому важное значение имеет понятие
мощности тока. Мощность тока равна
работе тока за единицу времени:
![]() .
.
При соединении приборов или проводников необходимо помнить следующее:
при параллельном соединении напряжение на всех приборах одинаковое и наибольшую мощность будет потреблять и, соответственно, выделять большее количество теплоты прибор с наименьшим сопротивлением.
при последовательном соединении наибольшую мощность будет потреблять прибор с наибольшим сопротивлением (т.к. ток одинаковый).
 От
формулы, определяющей тепло, выделяющееся
во всем проводнике, можно перейти к
формуле, характеризующей выделение
тепла в различных местах проводника.
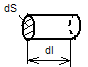
Выделим в проводнике объем в виде
цилиндра. За время dt в этом объеме,
согласно закону Джоуля-Ленца, выделится
теплота dQ
= I2Rdt
= (jdS)2
От
формулы, определяющей тепло, выделяющееся
во всем проводнике, можно перейти к
формуле, характеризующей выделение
тепла в различных местах проводника.
Выделим в проводнике объем в виде
цилиндра. За время dt в этом объеме,
согласно закону Джоуля-Ленца, выделится
теплота dQ
= I2Rdt
= (jdS)2![]() = ρj2dSdldt
= ρj2dVdt.
= ρj2dSdldt
= ρj2dVdt.
Qуд
=
![]() ,
,
![]() Qуд
= ρj2
- закон Джоуля-Ленца в дифференциальной
форме.
Qуд
– удельная тепловая мощность тока
(тепло, выделяющееся в единице объема
в единицу времени). Так как
j = σE, то
Qуд
= ρ(σE)2
= σE2.
Qуд
= ρj2
- закон Джоуля-Ленца в дифференциальной
форме.
Qуд
– удельная тепловая мощность тока
(тепло, выделяющееся в единице объема
в единицу времени). Так как
j = σE, то
Qуд
= ρ(σE)2
= σE2.
Лекция 7 Закон Ома для замкнутой цепи
Если в проводнике создать электрическое поле и не принять меры для его поддержания, то перемещение носителей заряда приведет к тому, что разность потенциалов между концами проводника будет уменьшаться и электрическое поле быстро исчезнет. Для того, чтобы поддерживать ток длительное время, нужно от одного конца проводника отводить приносимые туда заряды, а к противоположному концу непрерывно их подводить. Т.е., необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути. В этом случае в замкнутой цепи всегда будет участок, на котором перенос зарядов происходит против сил электростатического поля. Перемещение зарядов на этом участке возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами. Сторонние силы действуют в источниках тока.
П рирода
сторонних сил может быть различной. В
электрофорной машине разделение зарядов
происходит за счет механической работы.
В гальванических элементах и аккумуляторах
– за счет энергии химической реакции.
В фотоэлементах – за счет энергии света.
В генераторах заряды разделяются силами
магнитного поля.
рирода
сторонних сил может быть различной. В
электрофорной машине разделение зарядов
происходит за счет механической работы.
В гальванических элементах и аккумуляторах
– за счет энергии химической реакции.
В фотоэлементах – за счет энергии света.
В генераторах заряды разделяются силами
магнитного поля.
Действие сторонних
сил характеризуется физической величиной,
называемой электродвижущей силой (ЭДС).
ЭДС в замкнутом контуре численно равна
работе сторонних сил по перемещению
единичного положительного заряда вдоль
этого контура:
![]()
=
=
![]() .
.
Р ассмотрим
простейшую цепь, состоящую из источника
тока и резистора сопротивлениемR.
Источник тока имеет ЭДС
и внутреннее сопротивление r.
За время t
через поперечное сечение проводника
пройдет заряд Dq.
Тогда работа сторонних сил будет
ассмотрим
простейшую цепь, состоящую из источника
тока и резистора сопротивлениемR.
Источник тока имеет ЭДС
и внутреннее сопротивление r.
За время t
через поперечное сечение проводника
пройдет заряд Dq.
Тогда работа сторонних сил будет
![]() .
При совершении этой работы на внешнем
и внутреннем сопротивлении выделяется
теплота. По закону Джоуля-Ленца:
.
При совершении этой работы на внешнем
и внутреннем сопротивлении выделяется
теплота. По закону Джоуля-Ленца:![]() .
По закону сохранения энергии Аст
= Q.
.
По закону сохранения энергии Аст
= Q.
![]() или
или
![]() ,
,
![]() .
Сила тока в
замкнутой цепи равна отношению ЭДС цепи
к ее полному сопротивлению.
Это закон Ома для замкнутой цепи.
.
Сила тока в
замкнутой цепи равна отношению ЭДС цепи
к ее полному сопротивлению.
Это закон Ома для замкнутой цепи.
Е![]() сли
цепь содержит несколько источников
ЭДС, то полная ЭДС цепи равна алгебраической
сумме ЭДС отдельных источников. Если
ЭДС способствует движению положительных
носителей заряда в выбранном направлении,
то ЭДС считается положительной, если
препятствует – то ЭДС отрицательна. На
рисунке показано, при каком направлении
ЭДС считается положительной.
сли
цепь содержит несколько источников
ЭДС, то полная ЭДС цепи равна алгебраической
сумме ЭДС отдельных источников. Если
ЭДС способствует движению положительных
носителей заряда в выбранном направлении,
то ЭДС считается положительной, если
препятствует – то ЭДС отрицательна. На
рисунке показано, при каком направлении
ЭДС считается положительной.
Для внешней цепи
U
= IR
=![]() .
ПриR
= 0 (короткое замыкание) U
= 0, ток короткого замыкания
.
ПриR
= 0 (короткое замыкание) U
= 0, ток короткого замыкания
![]() .
ПриR
= ∞, U
= ε.
.
ПриR
= ∞, U
= ε.
