Государственное образовательное учреждение высшего профессионального образования «Сибирский государственный медицинский университет Федерального агентства по здравоохранению и социальному развитию»

(ГОУ ВПО СибГМУ Росздрава)

Кафедра___________________________

Утверждено

На заседании кафедры

Протокол №___от « «_______2009

Ст. преподаватель Колубаева Л.А.

ЛЕКЦИЯ №3

« Преломляющие оптические системы»

Преломляющие оптические системы дают возможность коррекции зрения.

Содержание

1.Преломление на двух сферических поверхностях. Правило знаков.

2.Формула тонкой линзы. Правило знаков. Оптическая сила линзы. Системы линз.

3.Построение изображений в линзах, использование побочных осей при построении. Увеличение линз.

4.Аберрации линз: сферическая, хроматическая, астигматическая.

5.Оптическая система глаза.

6.Аккомадация, адаптация, угол зрения, острота зрения.

Литература

1.Ландсберг Оптика

2. . Джанколи Д. Физика.Т.2; М. Мир, 1989г

3.Мякишев Т.Я. Физика, Оптика; М. Дрофа, 2002г

4. Федорова В. Н., Степанова Л. А. Краткий курс медицинской и биологической физики с элементами реабилитологии.

Лекции и семинары: Учебное пособие. — М.: ФИЗМАТЛИТ, 2005. —

624 с. - ISBN 5-9221-0568-Х.

Наглядные пособия

1. Компьютерные демонстрации

2. Презентации

Преломление на сферической поверхности. Формула линзы

Две поверхности линзы не всегда имеют одинаковый радиус кривизны. Поэтому возникает вопрос: может быть, и фокусы линзы, даже тонкой, не симметричны? Для ответа на него сначала рассмотрим преломление света на сферической поверхности.

Пусть источник света S находится в воздухе (показатель преломления которого считаем равным единице) на расстоянии d от выпуклой сферической стеклянной поверхности с показателем преломления п. Рассмотрим преломление световых лучей на сферической поверхности, полагая, что эти лучи являются параксиальными. Оптический ход всех преломленных лучей подчиняется закону Снелля.

Выберем луч, падающий на сферическую поверхность под углом , и построим преломленный луч (см. рисунок 3.1), восстановив в точку падения перпендикуляр. Этот перпендикуляр обязательно пройдет через центр кривизны зеркала

. (3.1)

Так как световые пучки параксиальны, то углы  и - малы, формулу (3.1) можно записать следующим образом:

. (3.2)

Внешний угол треугольника равен сумме двух внутренних, поэтому

и. (3.3)

Выразим углы ичерез эти углы из равенств (3.3) и подставим в равенство (3.2),

Получим

или

. (3.4)

Рис.3.1

ОР=R-радиус преломляющей поверхности Углы,,опираются на одну и ту же дугу и малы, поэтому

; ;.

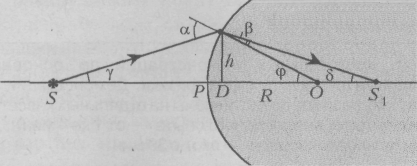
Подставим полученные выражения в уравнение (3.4) и сократим h, тогда

. (3.5)

Рис.3.2

Мы получили уравнение, которое может применяться к любому лучу, падающему на сферическую преломляющую поверхность, так как нет зависимости от угла падения, поэтому точкуS₁можно считать изображением точкиS.

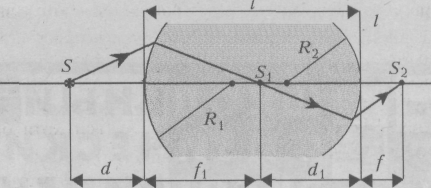
Теперь рассмотрим линзу толщиной l и радиусами кривизны сферических поверхностей R₁ и R₂.

Применив формулу (3.5) для обеих поверхностей, соответственно получим систему уравнений:

и.

Решаем эту систему

или

.

В тонкой линзе вершины совпадают, поэтому для тонкой линзы выполняется условие , получаем

.

Фокусом линзы является точка, в которой сходится параллельный пучок лучей после преломления. Параллельный пучок световых лучей можно получить от бесконечно удаленного источника света (d=), тогда его изображение получится в фокусе, т.е.f=F. Если учесть, что линза может находиться в любой среде, то показатель преломленияn- это уже относительный показатель преломления, поэтому окончательно можем записать:

, (3.6)

где n_лин.- показатель преломления материала линзы, а n_ср.- показатель преломления среды, в которой находится линза; R₁, R₂- радиусы сферических поверхностей линзы.Знаки у радиусов кривизны определяются следующим правилом: радиус кривизны считается положительным, если свет падает на выпуклую поверхность и отрицательным, если свет падает на вогнутую поверхность.

Из этой формулы (3.6)видно, что перемена местами R₁и R₂(равносильная перевертыванию линзы на 180) не влияет на вычисляемое значение фокусного расстояния F. Также эта формула показывает, что одна и та же линза, находясь в разных средах, может быть и собирающей и рассеивающей, кроме того, передний и задний фокусы могут быть не симметричными относительно оптического центра линзы.

Обратите внимание, что для плоской поверхности R=.