
Государственное образовательное учреждение высшего профессионального образования «Сибирский государственный медицинский университет Федерального агентства по здравоохранению и социальному развитию»
(ГОУ ВПО СибГМУ Росздрава)
Кафедра___________________________
Утверждено
На заседании кафедры
Протокол №___от « «_______2009
Ст. преподаватель Колубаева Л.А.
ЛЕКЦИЯ №5
« Интерференция света. Пространственная и временная когерентность»
Томск-2009
Содержание
1.Методы получения когерентных волн.
2.Описание интерференционной картины и ее анализ.
3.Распределение интенсивности в интерференционной картине. Видность интерференционной картины.
4.Волновой цуг. Пространственная и временная часть фазы волны.
5.Влияние немонохроматичности света на интерференционную картину, временная когерентность.
Литература
1.Трофимова Т.И., Курс физики, М, Высшая школа, 1997г.
2.Савельев И.В. Курс общей физики т.3 М.изд. Дрофа,2003г.
3.Калитеевский Н.И., Волновая оптика, М., изд. Наука,1986г.
4.Иродов И.Е. Волновые процессы. Основные законы. М.Высшая школа,1990г.
Наглядные пособия
1.Компьютерные демонстрации
2.Презентации.
Методы получения когерентных световых волн
Вернемся к вопросу, который обсуждался уже в лекции 4.Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны — неограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников, например от двух электрических лампочек. Понять физическую причину немонохроматичности, а, следовательно, и некогерентности волн, испускаемых двумя независимыми источниками света, можно исходя из самого механизма испускания света атомами. В двух самостоятельных источниках света атомы излучают независимо друг от друга. В каждом из таких атомов процесс излучения конечен и длится очень короткое время (10~8с). За это время возбужденный атом возвращается в нормальное состояние и излучение им света прекращается. Возбудившись вновь, атом
снова начинает испускать световые волны, но уже с новой начальной фазой. Так как разность фаз между излучением двух таких независимых атомов изменяется при каждом новом акте испускания, то волны, спонтанно излучаемые атомами любого источника света, некогерентны. Таким образом, волны, испускаемые атомами, лишь в течение интервала времени 10~8с имеют приблизительно постоянные амплитуду и фазу колебаний, тогда как за больший промежуток времени и амплитуда, и фаза изменяются.
Получить когерентные волны можно двумя способами: делением фронта волны и делением амплитуды. Оба способа сводятся к делению одной волны на две. К первому способу относятся, опыты Юнга на двух щелях, зеркала Френеля, бипризма Френеля
Рис.5.1
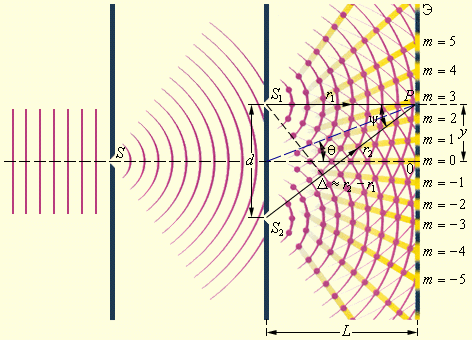
Рис.5.2

![]() имеют одну общую грань. Параллельно
этой грани, на расстоянии а от нее,
располагается прямолинейный источник
светаS. Можно показать,
что в случае, когда преломляющий угол
имеют одну общую грань. Параллельно
этой грани, на расстоянии а от нее,
располагается прямолинейный источник
светаS. Можно показать,
что в случае, когда преломляющий угол![]() призмы
очень мал и углы падения лучей на грань
призмы не очень велики, все лучи
отклоняются призмой на практически
одинаковый угол. Угол падения лучей на
бипризму невелик. Поэтому все лучи
отклоняются каждой из половин бипризмы
на одинаковый угол. В результате
образуются две когерентные цилиндрические
волны, исходящие из мнимых источниковS1иS2,
лежащих в одной плоскости сS(рис.5.2).
призмы
очень мал и углы падения лучей на грань
призмы не очень велики, все лучи
отклоняются призмой на практически
одинаковый угол. Угол падения лучей на
бипризму невелик. Поэтому все лучи
отклоняются каждой из половин бипризмы
на одинаковый угол. В результате
образуются две когерентные цилиндрические
волны, исходящие из мнимых источниковS1иS2,
лежащих в одной плоскости сS(рис.5.2).
Рис.5.3
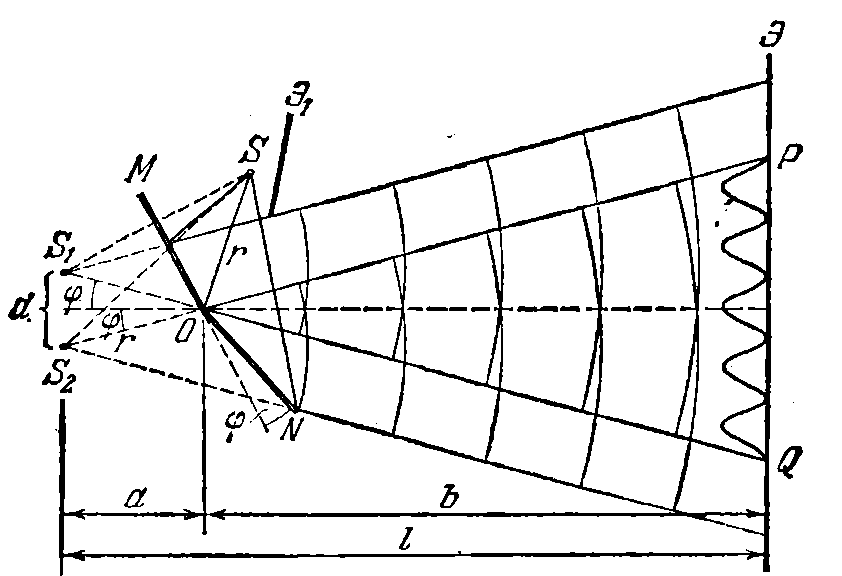
Зеркала Френеля.Два плоских соприкасающихся зеркала ОМ иONрасполагаются так, что их отражающие поверхности образуют угол, близкий кСоответственно уголна рисунке очень мал. Параллельно линии 'пересечения зеркал О на расстоянии г от нее помещается прямолинейный источник светаS(например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы Они исходили из мнимых источниковS1иS2(рис.5.3)
Описание интерференционной картины и ее анализ .
Рис.5.4

Пусть источники StиS2 являются когерентными и получены одним из перечисленных методов.
Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников StиS2, имеющих вид параллельных тонких светящихся нитей либо узких щелей (рис.5.4). Область, в которой эти волны перекрываются, называется полем интерференции. Во всей этой области наблюдается чередование мест с максимальной и минимальной интенсивностью света. Если в поле интерференции внести экран, то на нем будет видна интерференционная картина, которая имеет вид чередующихся светлых и темных полос. Вычислим ширину этих полос в предположении, что экран параллелен плоскости, проходящей через источники S1иS2. Положение точки на экране будем характеризовать координатой х, отсчитываемой в направлении, перпендикулярном к линиям S1иS2.. Начало отсчета выберем в точке О, относительно которой S1иS2. расположены симметрично. Источники будем считать колеблющимися в одинаковой фазе. Из рис. 5.4 видно, что
![]()
Следовательно,
![]()
Ниже будет выяснено, что для получения
различимой интерференционной картины
расстояние между источниками d должно
быть значительно меньше расстояния до
экрана l. Расстояние х, в
пределах которого образуются
интерференционные полосы, также бывает
значительно меньшеl. При
этих условиях можно положить![]() ,
тогда
,
тогда
![]()
Умножив s2-s1на показатель преломления средыn, получим оптическую разность хода
![]() (5.1)
(5.1)
Подстановка этого значения разности хода в условие максимума
![]()
дает, что максимумы интенсивности будут наблюдаться при значениях х, равных
![]() (5.2)
(5.2)
Здесь
![]() —
длина волны в среде, заполняющей
пространство между источниками и
экраном.
—
длина волны в среде, заполняющей
пространство между источниками и
экраном.
Подставив значение (5.1) в условие
![]()
получим координаты минимумов интенсивности:
![]() (5.3)
(5.3)
Назовем расстояние между двумя соседними максимумами интенсивности расстоянием между интерференционными полосами, а расстояние между соседними минимумами интенсивности — шириной интерференционной полосы. Из формул (5.2) и (5.3) следует, что расстояние между полосами и ширина полосы имеют одинаковое значение, равное
![]() (5.4)
(5.4)
Согласно формуле (5.4) расстояние между полосами растет с уменьшением расстояния между источниками d. При d, сравнимом с lрасстояние между полосами было бы того же порядка, что ит. е. составляло бы несколько десятых мкм. В этом случае отдельные полосы были бы совершенно неразличимы. Для того чтобы интерференционная картина стала отчетливой, необходимо соблюдение упоминавшегося выше условия: d<<l.
