ЛЕКЦИЯ№16

« Строение атома»

Введение

К атомной физике относятся вопросы строения атомов и изучение явлений, обусловленных свойствами и процессами в атомных оболочках.

Содержание

1.Эффект Комптона.

2.Волновая природа материи. Гипотеза Луи-де-Бройля.

3.Модели атомов. Атомные спектры.

4.Постулаты Бора.

5.Элементарная теория атома водорода по Бору.

Литература

1Савельев И.В. Курс общей физики т.3,4. М.изд. Дрофа,2003г.

2 Матвеев А.Н. Атомная физика, М., изд. Высшая школа, 1989г

3.Шпольский Э.В. Атомная физика, т 1,2, М. изд.Наука, 1974г

Наглядные пособия

1.Компьютерные демонстрации

2.Презентации.

Эффект Комптона.

Обсуждается экспериментальное доказательство правильности формул, связывающих энергию и импульс фотона с частотой и волновым вектором электромагнитных волн.

Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название эффекта Комптона. В 1923 г. Комптон '), исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах наряду с излучением первоначальной длины волны содержатся также лучи большей длины волны. Разность=-оказалась зависящей только от углаQ, образуемого направлением рассеянного излучения с направлением первичного пучка. От длины волны направлением первичного пучка. От длины волныи природы рассеивающего веществане зависит.

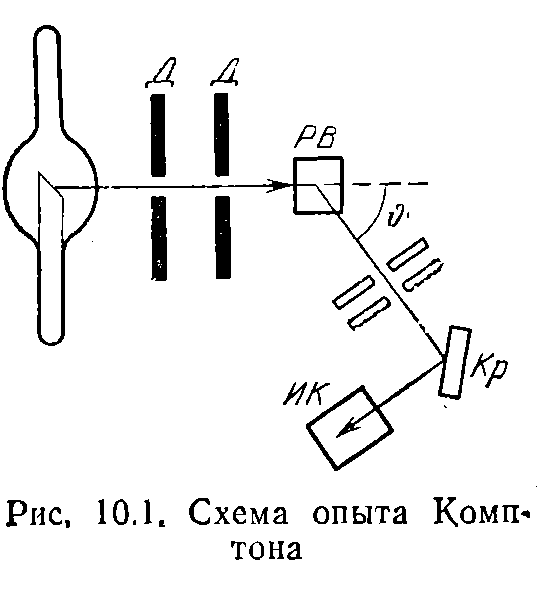
Схема опыта Комптона показана на рис. 10.1. Выделяемый диафрагмами Д узкий пучок монохроматического (характеристического) рентгеновского излучения направлялся на рассеивающее вещество РВ. Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из кристалла Кр и ионизационной камеры ИК.

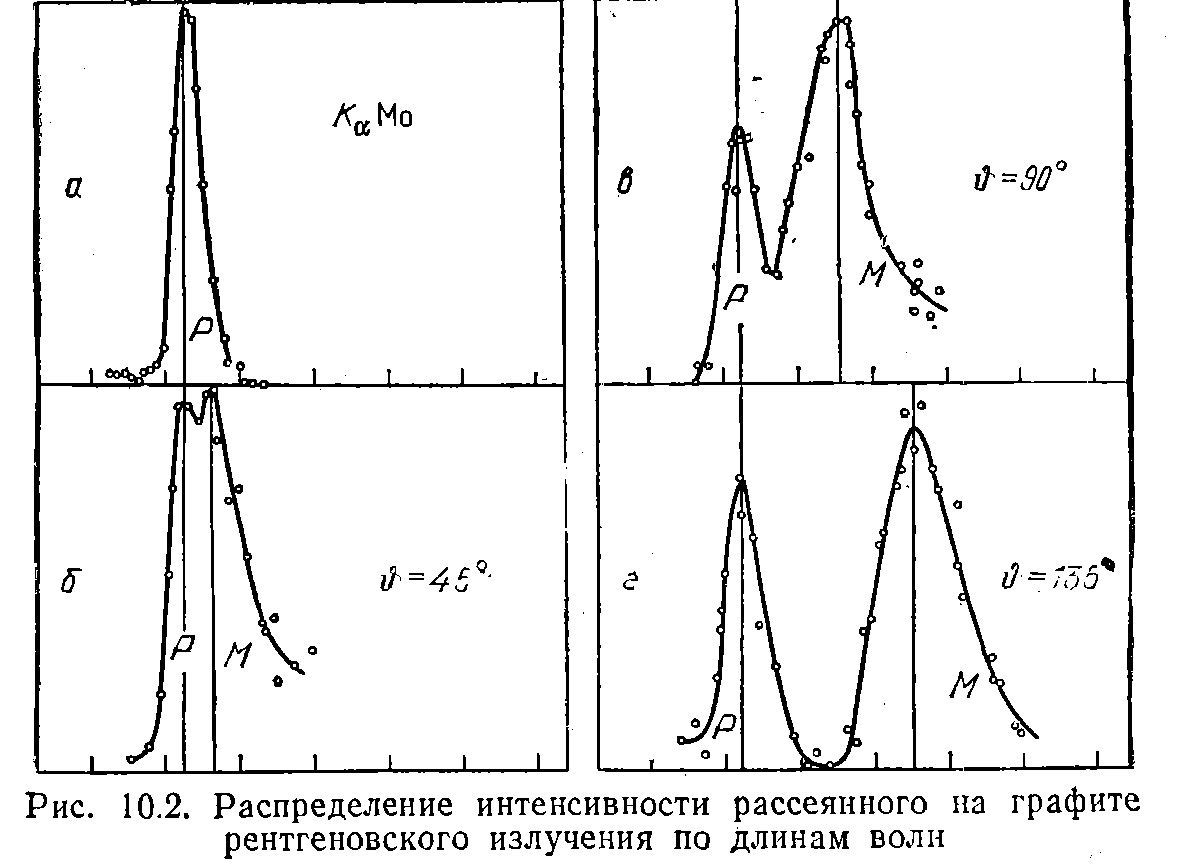
На рис. 10.2 приведены результаты исследования рассеяния монохроматического рентгеновского излучения на графите. Кривая а характеризует первичное излучение. Остальные кривые относятся к разным углам рассеяния Q, значения которых указаны на рисунке. По оси ординат отложена интенсивность излучения, по оси абсцисс — длина волны.

При рассеянии веществами с малым атомным номером (Li, Be, В) практически все рассеянное излучение имеет смещенную длину волны. По мере увеличения атомного номера все большая часть излучения рассеивается без изменения длины волны. Все особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Свободными можно считать слабее всего связанные с атомами электроны, энергия связи которых значительно меньше той энергии, которую фотон может передать электрону при соударении. Пусть на первоначально покоящийся свободный электрон падает фотон с энергией и импульсом(рис. 10.4).

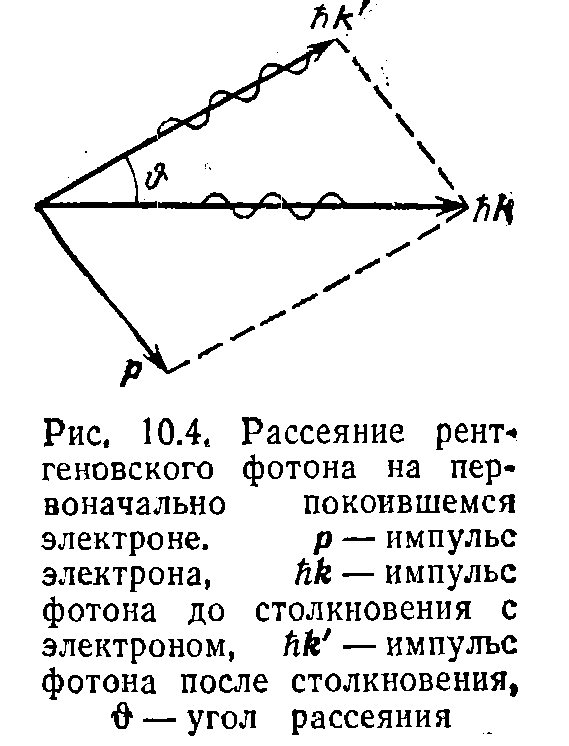
Энергия электрона до столкновения равна mc²(m— масса электрона), импульс равен нулю. После столкновения электрон будет обладать импульсом р и энергией, равной. Энергия и импульс фотона также изменятся и станут равнымии. Из законов сохранения энергии и импульса вытекают два равенства:

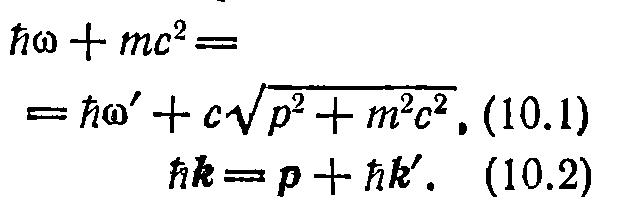
Разделим первое равенство на с и напишем его в виде –

Возведение в квадрат дает

Из 10.3 следует, что

(-угол между векторамиkиkсм рис.10.4)

Из сравнения выражений 10.3 и 10.4 получаем

Умножим это равенство на 2и разделим наmckk:

Наконец, учтя, что 2/k =, придем к формуле

(10.5)

Определяемая этим выражением величина _сназывается комптоновской длиной волны той частицы, массаmкоторой имеется в виду. В рассматриваемом нами случае_c— комптоновская длина волны электрона. Подстановка значенийдает для_cэлектрона значение

(Комптоновской длиной волны называют иногда величину . Для электрона_с= 0,000386 нм.)

Результаты измерений Комптона и последующих измерений находятся в полном согласии с формулой (10.5), если подставить в нее значение (10.7) для _с. При рассеянии фотонов на электронах, связь которых с атомом велика, обмен энергией и импульсом происходит с атомом как целым. Поскольку масса атома намного превосходит массу электрона, комптоновское смещение в этом случае ничтожно и' практически совпадает с. По мере роста атомного номера увеличивается относительное число электронов с сильной связью, чем и обусловливается ослабление смещенной линии (см. рис. 10.3).

Волновая природа материи. Гипотеза Луи-де-Бройля.

В 1923 г. Луи де Бройль расширил представление о корпускулярно-волновом дуализме. Глубоко осознав существующую в природе симметрию, он высказал гипотезу о том, что поскольку свет ведет себя в одних случаях как волна, а в других как частица, то и объекты, которые мы считаем материальными частицами (электроны и другие элементарные частицы), могли бы обладать волновыми свойствами. Де Бройль предположил, что длина волны, отвечающая частице, связана с ее импульсом так же, как в случае фотона, т.е. . Иначе говоря, длина волны, отвечающая частице с массойm, которая движется со скоростью, определяется формулой

Величину иногда называют де-бройлевской длиной волны частицы. Это чрезвычайно малая длина волны. Даже при крайне низких скоростях, т.е. дебройлевскую длину волны вследствие ее малости сложно обнаружить и измерить. Дело в том, что типичные волновые явления- интерференция и дифракция- проявляются только тогда, когда размеры предметов или щелей сравнимы по своей величине с длиной волны. Но нам не известны предметы или щели, на которых могли бы дифрагировать волны с длиной волны 10^-30м, поэтому волновые свойства обычных тел обнаружить не удается.

Если же речь идет о крошечных элементарных частицах типа электронов, которые имеют массу m=9,1*10^-31кг и допустим задать им скоростьм/с, то длина волныпропорциональна 10^-10м, несмотря на то, что это очень короткие длины волн, тем не менее их можно обнаружить экспериментально: межатомные расстояния в кристаллах того же порядка, что и данная длина волны, и регулярно расположенные атомы в кристалле можно использовать в качестве дифракционной решетки.

Опыты Дэвидсона и Джермера.

Дэвидсон и Джермер наблюдали отражение электронного пучка от поверхности кристалла. В первом опыте на монокристалл никеля направляли электроны с энергией в несколько десятков электрон-вольт. Затем, изменяя угол падения электронов на поверхность кристалла, фиксировали изменение интенсивности отраженного пучка. Зависимость интенсивности отраженного

пучка от угла скольжения а показана на рис. 35. На полярной диаграмме отчетливо виден максимум интенсивности отражения при угле ₀.

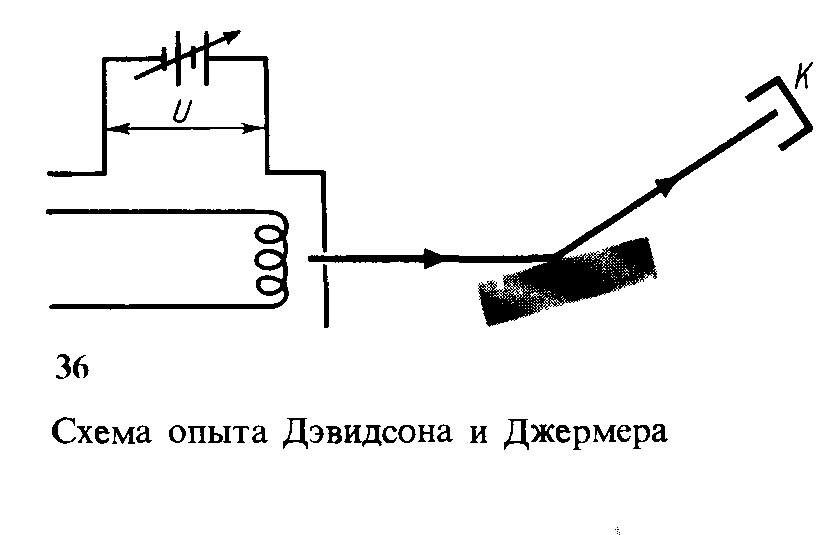
Во втором опыте при фиксированном угле падения электронного пучка на кристалл измерялась интенсивность отраженного пучка в зависимости от энергии Интенсивность пучка отраженных электронов измерялась по силе тока от коллектора электронов К (рис. 36).

Результаты эксперимента показаны на рис. 37.

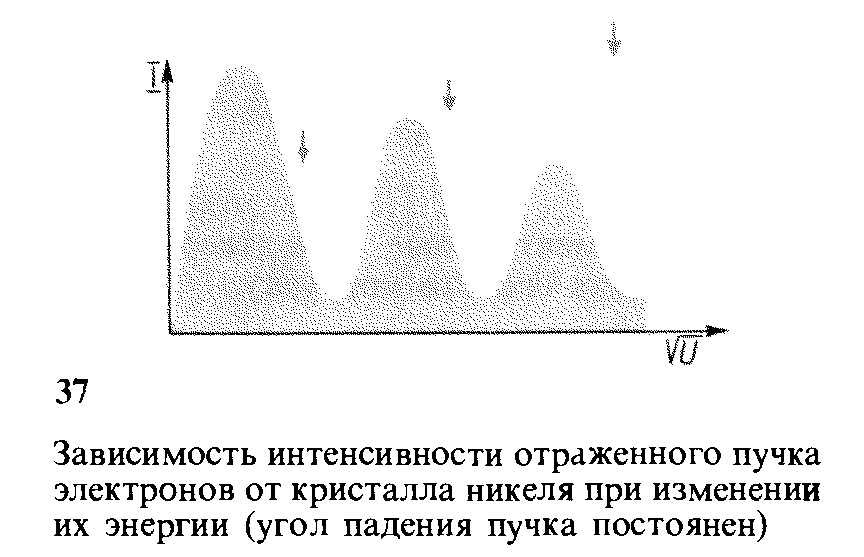
Результаты опытов Дэвидсона и Джермера получили объяснение (1927) как проявление волновой природы электронов и дали количественное подтверждение справедливости формул де Бройля.

В теоретическом плане анализ дифракции электронных волн полностью совпадает с дифракцией рентгеновских лучей. Расчет длины волны по дифракционной картине совпадает с длиной волны предсказанной Луи-де- Бройля.

Опыты Томсона и Тартаковского.

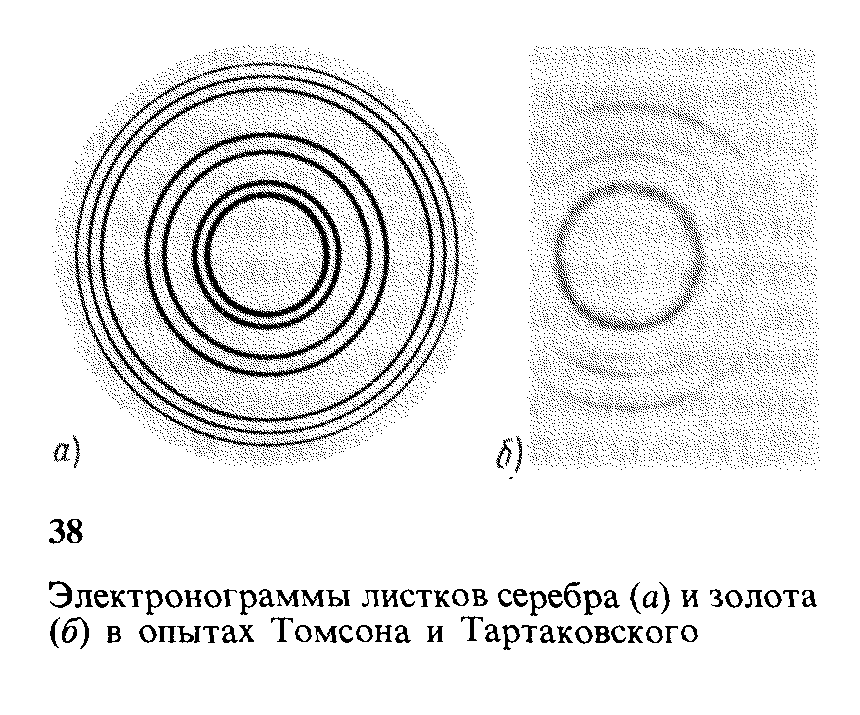
Для наблюдения дифракции электронов Томсон и Тартаковский пропускали пучок электронов через металлическую поликристаллическую пластину рассеянные электроны должны дать на фотографической пластинке систему интерференционных колец. В опытах Томсона и Тартаковского такая система интерференционных колец действительно наблюдалась. Однако для объяснения результата этих опытов возможно предположение, что система интерференционных колец порождается не рассеянными электронами, а вторичным рентгеновским излучением, возникающим в результате падения пучка электронов на пластину. Для того чтобы убедиться в ошибочности такого предположения, на пути рассеянных электронов между металлической пластинкой и фотопластинкой создается дополнительное магнитное поле. Оно не влияет на рентгеновское излучение и, следовательно, не должно искажать интерференционной картины, если она порождается рентгеновским излучением. Если же интерференционная картина порождается рассеянными электронами, то магнитное поле должно ее исказить. Такого рода проверка показала, что дифракционная картина обусловливается именно электронами, а не вторичным рентгеновским излучением. Г. П. Томсон осуществил опыты с быстрыми электронами (17,5-56,5 кэВ), а П. С. Тартаковский - со сравнительно медленными (до 1,7 кэВ). Вид электронограмм листков серебра и золота приведен на рис. 38. Количественный анализ результатов опытов полностью подтвердил правильность уравнений де Бройля.

Модели атомов. Атомные спектры

Атомные спектры

Излагаются экспериментальные закономерности атомных спектров и анализируется их несовместимость с классическими представлениями об излучении

Возбуждение спектров излучения. Материальные тела являются источниками электромагнитного излучения. В принципе существует два вида излучения, различающихся способом их возбуждения: 1) тепловое излучение; 2) различные виды люминесценции: а) электролюминесценция, б) хемилюминесценция, в) флуоресценция. Тепловое излучение возникает в результате нагревания тел. При столкновении друг с другом атомы и молекулы приобретают энергию, переходя в возбужденное состояние. Затем эту энергию они излучают. Таким образом, источником энергии при тепловом излучении является кинетическая энергия теплового движения атомов и молекул. Люминесценцией называются все виды испускания света, в которых кинетическая тепловая энергия несущественна для механизма возбуждения. Электролюминесценцией называется свечение в электрических разрядах всех видов. Хемилюминесцещией называется излучение, когда возбуждение атомов происходит в результате химических реакций. Флуоресценция -это излучение атомов, возбужденных в результате поглощения света.

Во второй половине 19 столетия были проведены многочисленные и тщательные исследования спектров излучения. Оказалось, что спектр излучения молекул состоит из широких размытых полос без резких границ. Такого рода спектры были названы полосатыми. Спектр излучения атомов имеет совсем другой вид. Он состоит из отдельных, резко обозначенных линий. В связи с этим спектры атомов были названы линейчатыми. Для каждого элемента имеется вполне определенный излучаемый им линейчатый спектр. Вид линейчатого спектра не зависит от способа возбуждения атома. По спектру можно определить элемент, которому он принадлежит. Линии в спектрах располагаются закономерно. Найти закономерности расположения линий излучения в линейчатых спектрах и объяснить эти закономерности было важнейшей задачей физического исследования. Первые шаги были сделаны в направлении подбора эмпирических формул, которые бы правильно описывали положение отдельных линий в спектрах. Первый удачный шаг был сделан Бальмером, нашедшим эмпирическую формулу для части линий излучения в спектре атома водорода.

Экспериментальные спектре атома водорода.

Экспериментальные закономерности в линейчатых спектрах. Анализ эмпирического материала по линейчатым спектрам показал, что отдельные линии в спектрах могут быть объединены в группы линий, которые принято называть сериями. Бальмер открыл (1885), что линии в видимой части спектра водорода можно представить следующей простой формулой:

где R-постоянная величина, частота излучения соответствующей линии. Эта серия линий называется серией Балъмера. Лайман открыл (1906) другую серию линий, лежащую в ультрафиолетовой части спектра атома водорода: -

Эта серия называется серией Лаймана. Пашен открыл (1908) серию в ин-

инфракрасной части спектра атома водорода:

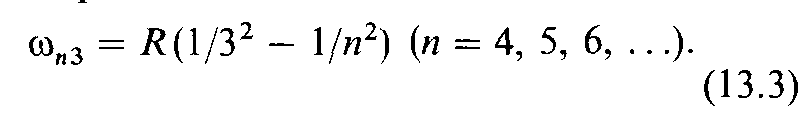
Эта серия называется серией Пашена. В дальнейшем в инфракрасной части спектра водорода были открыты также другие серии: серия Брэкета

серия Пфундта

Рассмотрение формул (13.1 — 13.5) для частот спектральных серий показывает, что каждая из частот является разностью двух величин, зависящих от целого числа. Если

то каждую излученную частоту можно представить в виде разности величин (13.6) при различных значениях целых чисел:

Серия линий получается по формуле (13.7), если одно из целых чисел фиксировано, а другое пробегает все целые значения, большие фиксированного целого числа.

Комбинационный принцип. Таким образом, излучение атома водорода

характеризуется величинами

которые называются спектральными термами. Все излучаемые частоты могут

быть представлены как комбинации спектральных термов вида (13.7). Это правило, сформулированное Ритцем (1908), называется комбинационным принципом Ритца. Исследование спектров более сложных атомов показало, что частоты линий их излучения также представляются в виде разностей спектральных термов, характерных для данного атома, но формулы для термов бывают несколько сложнее, чем формула (13.6) для атома водорода.